
本文是对Bengio的论文《 Understanding the difficulty of training deep deedforward neural networks》解读的第三部分。主要的内容:
1、不同初始化方法 下的梯度在反向传播中的表现
2、误差曲线和结论
接上文《深度学习里数学之----方差----美妙而富有韵味》
4.2.2梯度反向传播的研究
为了能够验证上面提出的理论观点,我们使用了两种不同的初始化方法,
并且得到了激活函数值、反向传播梯度梯度的归一化直方图。见图6、7、
8,实验结果是基于shapeset3*2得到的,类似地结果同样可以从其他数
据集上获得。
我们监测了第i层雅可比矩阵的奇异值变化:
当相邻的两层具有相同的维度时,平均奇异值对应于从映射到
的无穷小体积的平均比率,以及从映射到的平均激活值方差比率。
在使用规范化初始化方法下,比率在0.8附近,而在标准初始化方法下,该
值下降到0.5左右。
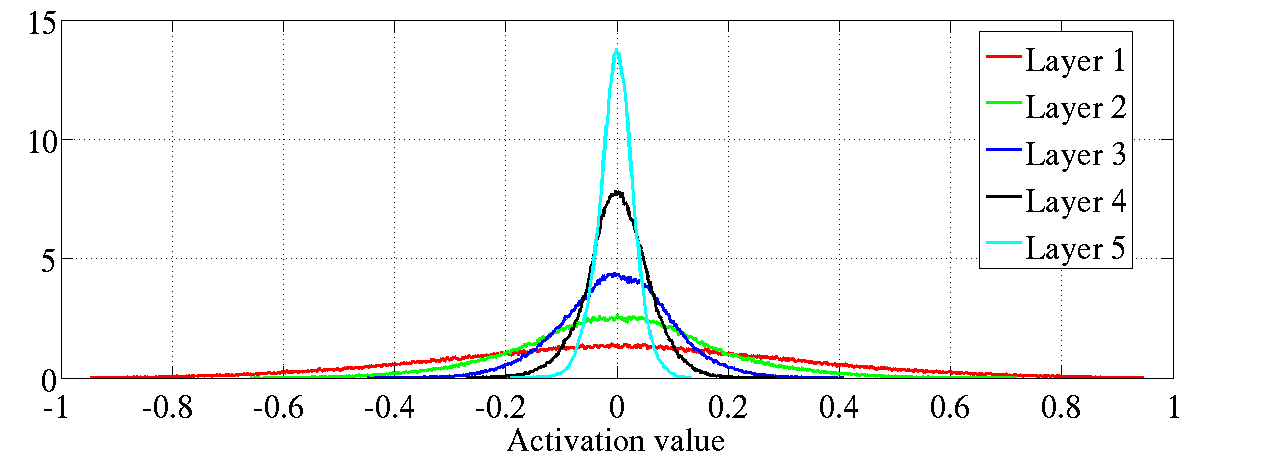
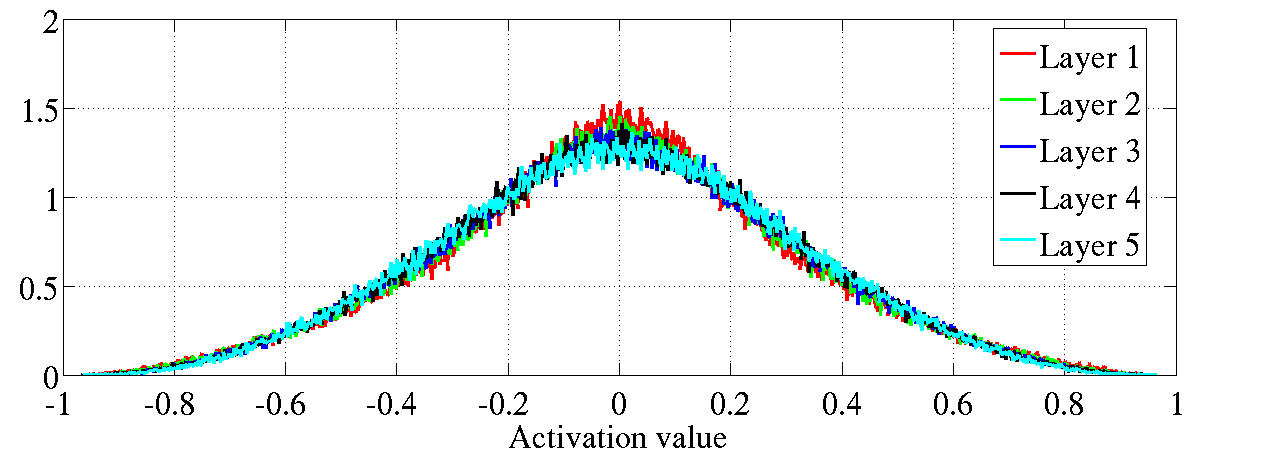
图6:双曲正切激活值归一化直方图,上图:标准化初始化方法;下图:规
范化初始化方法。上图:处于更高层的神经元在0峰值处的值在增加。
4.3梯度在学习过程中的反向传播
在深度神经网络中的动态学习过程是相当复杂的,我们需要开发出更好的工
具来分析和跟踪这种学习过程。特别地,在我们的理论分析中,我们不能使
用简单的方差计算,因为权重值与激活值不再是独立的,线性假设同样也是
违反的。
正如Bradley (2009)第一次提到的,我们发现( 图7)在训练的初始阶段,在标准初始化后,当向下传播时,反向传播梯度的方差会变的更小。但是,我们发现这种趋势在学习过程中会发生急速的转变。使用我们规范化初始化的方法,我们没有看到这样反向传播梯度的下降情况(图7 下半部分)。
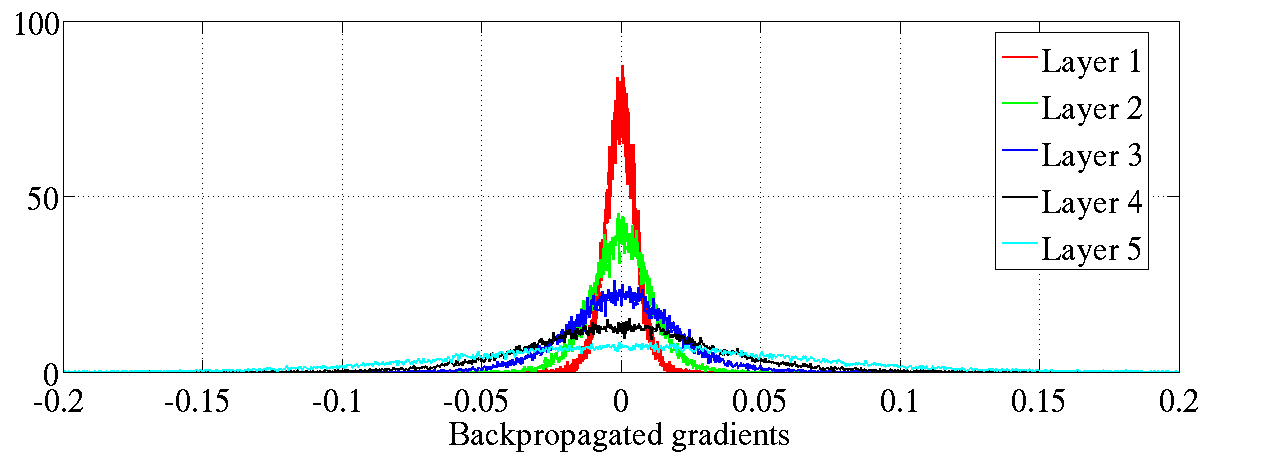
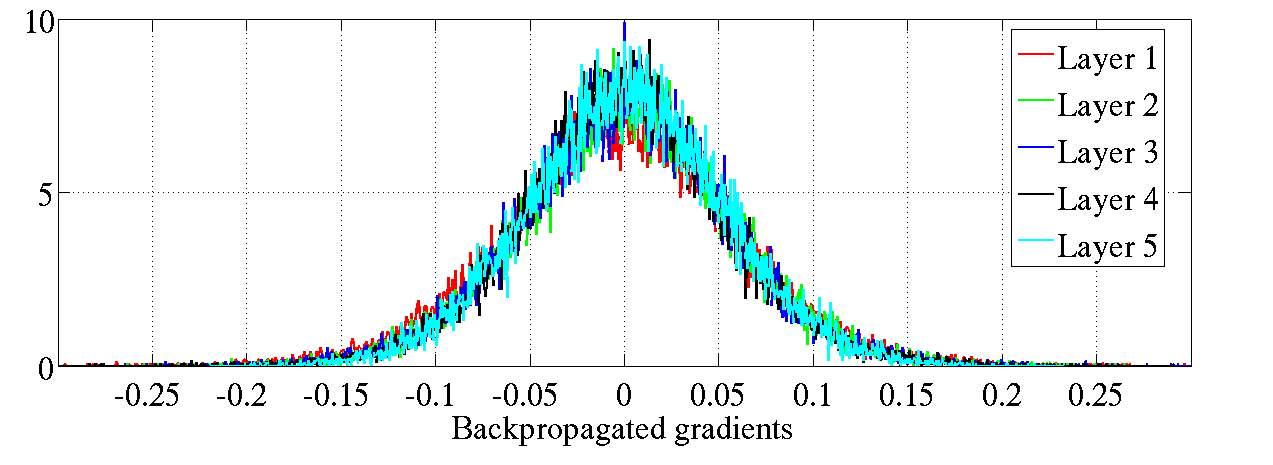
图7:双曲正切激活函数的反向传播归一化直方图,上图是标准初始化方法,下图是规范化初始化方法。上图:处于更高层的神经元在0 峰值处的值在下降。
起初真正惊讶的是即使当反向传播的梯度变小的时候,层之间权重系数的方差是大致保持不变的,如图8 所示。然而,这就是我们上面理论分析的解释。有趣地是,正如图9所示,这些经标准和规范化初始化的权重系数的梯度在训练阶段发生变化。的确,梯度最初具有大致相同的幅度,随着训练的进行,它们彼此发散(在较低层中具有较大的梯度),特别是在标准初始化的情形。注意,这可能是规范化初始化的优点之一,因为在不同层处具有非常不同大小的梯度可能导致训练异常和较慢训练。
最后,我们观察到softsign 网络与正态化初始化的tanh网络具有相似性,这可以通过比较两种情况下的激活演化过程看出(相应地,图3- 底部和图10)。
5、误差曲线和结论
我们关心的最后一个考虑点是不同的成功训练策略以及这些成功案例最好的阐述了随着训练的进展和渐进的发展,测试误差的变化情况。
图11展示了这样测试误差在线学习时的曲线变化,数据集时shapeset3*2,表1给出了所有数据集最后的测试误差。作为一个对比基准,我们在样本数为 100,000的shapeset数据集上优化了rbf svm模型,得到的测试误差是59.47%,在同样的数据集上,我们使用一个深度为 5、激活函数为tangent并且使用规范化初始化的深度神经网络获得的测试误差是50.47%。
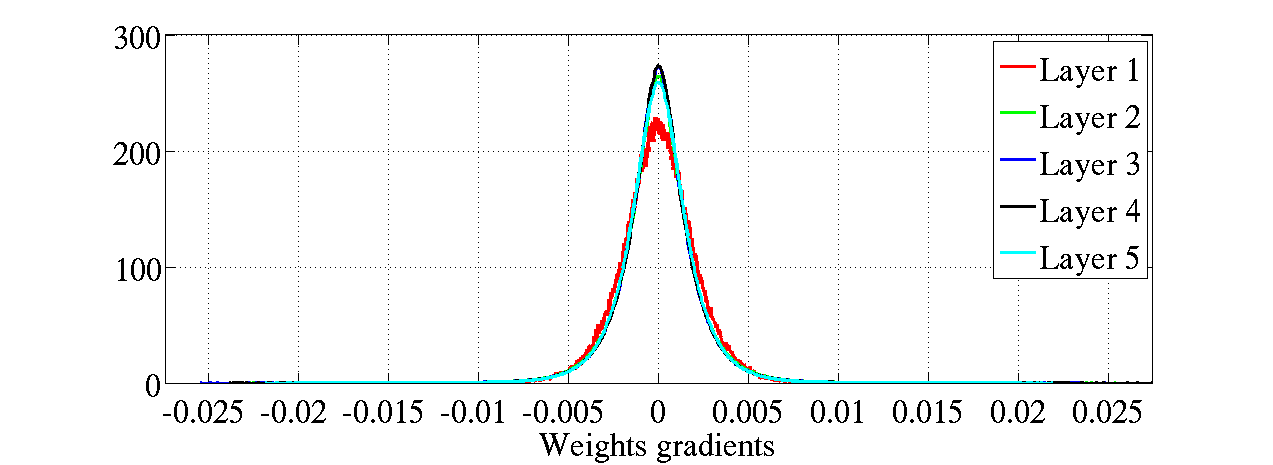
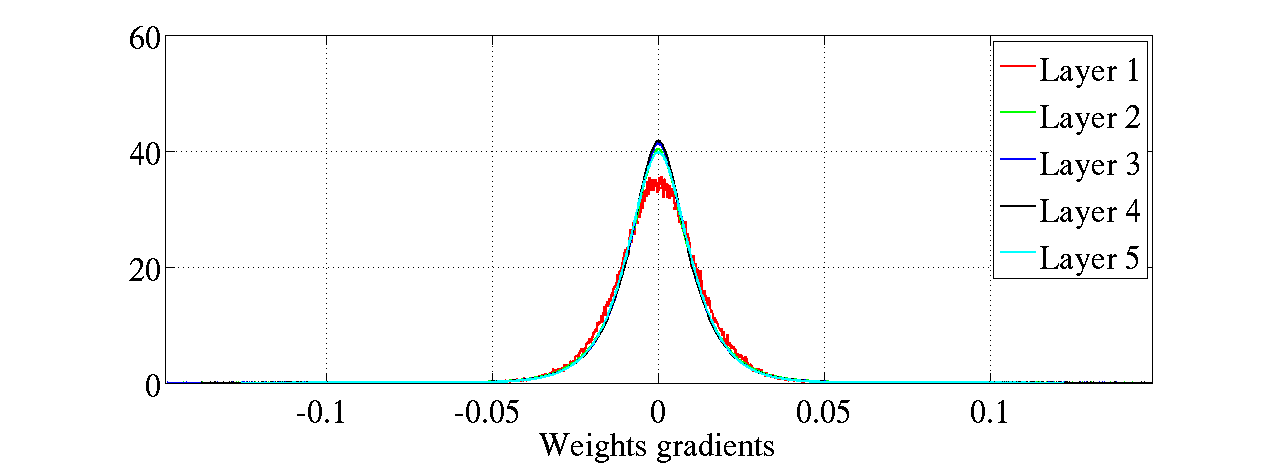
图8:不同初始化方法下的反曲正切激活函数的权重梯度归一化直方图,上图:标准初始化,下图:规范化初始化方法。即使在标准初始化下的反向传播梯度变得更小些,但是权重梯度并没有变的更小。
|
TYPE |
Shapeset |
MNIST |
CIFAR-10 |
ImageNet |
|
softsign |
16.27 |
1.64 |
55.78 |
69.14 |
|
Softsign N |
16.06 |
1.72 |
53.8 |
68.13 |
|
Tanh |
27.15 |
1.76 |
55.9 |
70.58 |
|
Tanh N |
15.60 |
1.64 |
52.92 |
68.57 |
|
Sigmoid |
82.61 |
2.21 |
57.28 |
70.66 |
表1:不同深度神经网络下的测试误差,其含有5层隐含层、激活函数函数不同以及不同的初始化机制。激活函数后面的 N表示其使用规范化初始化。
这些说明了激活函数、初始化的选择带来的影响。图11作为一个参考,经过消除自编码的无监督预训练初始化得到监督学习的微调误差曲线。对于每一个神经网络,各自选择不同学习率在验证集上来减小误差。我们可以得出结论,由于任务的不同,我们观察到学习过程中重要的饱和性,这也解释了规范化初始化或者softsign的影响是更加可见的。
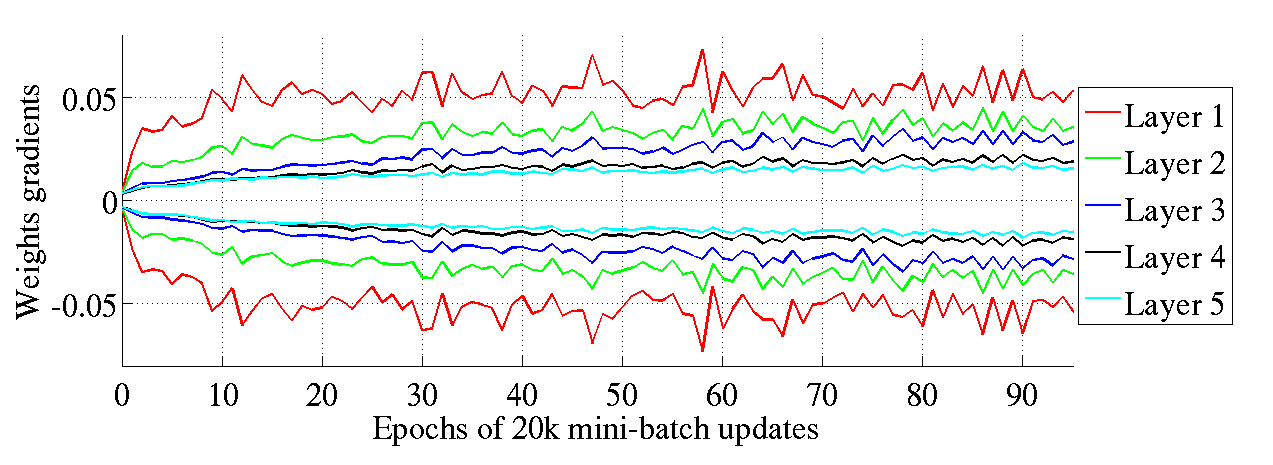
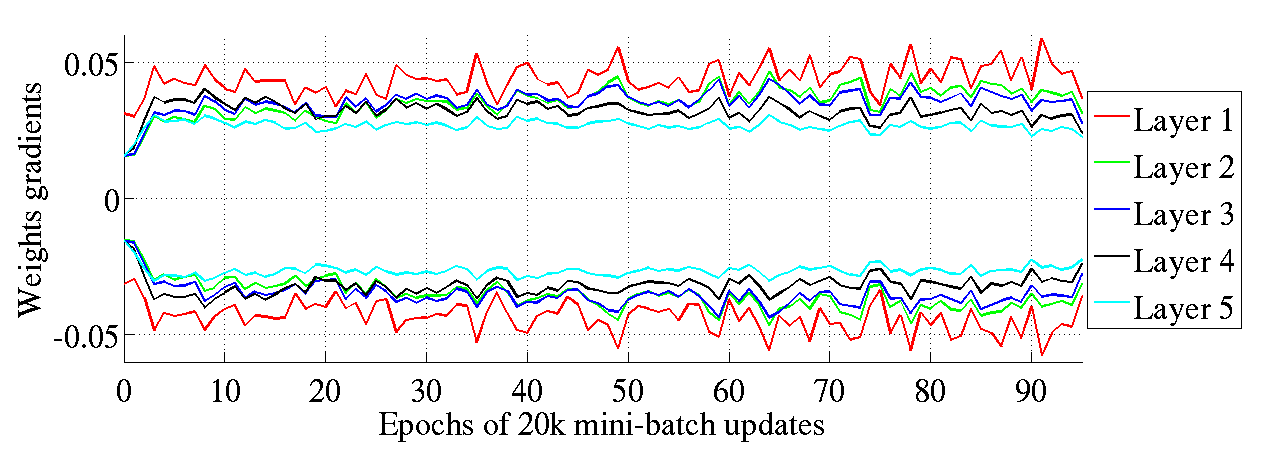
图9:训练过程中在不同初始化方法下的反曲正切激活函数的权重梯度的标准差区间。上图:标准初始化方法;下图:规范化初始化方法。我们可以看到规范化的权重梯度在层与层之间可以保持相同的方差(上图:网络的高层含有较小的方差)。
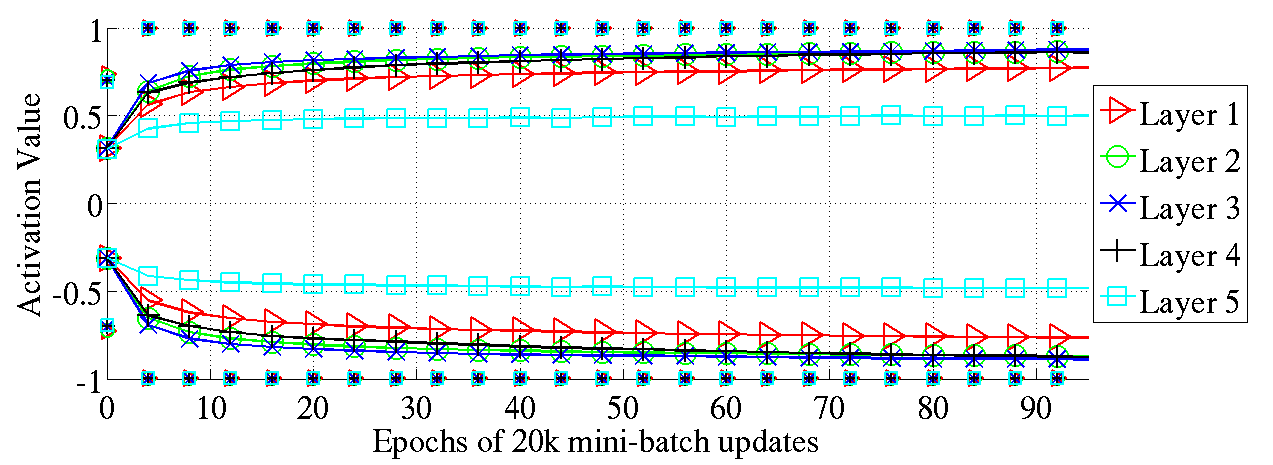
图10:89%的数据是单独记录的,由双曲正切函数在不同初始化方法下的分布得到的标准差(实现标记)。
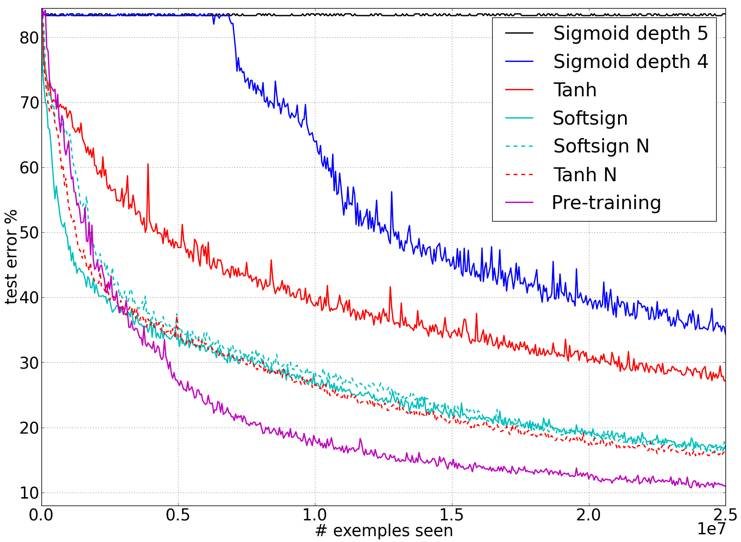
图11:误差曲线
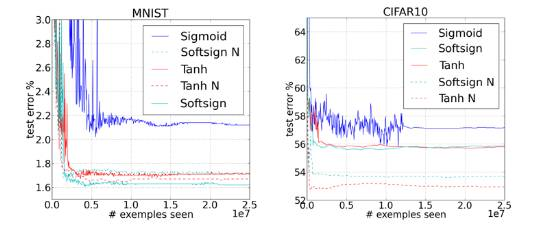
图12:误差曲线
从误差曲线可以得出一些结论:
1、越是经典的神经网络,且其激活函数是sigmod 、tangent、以及标准初始化,其收敛的速度越慢,并最终趋向于更低局部极小值。
2、相比于tanh ,softsign神经网络对于初始化机制似乎更加健壮,大概的原因可能是因为其更为一般的非线性行。
3、对于tanh 网络,已提出的规范化初始化方法可以得很很好的帮助,大概是因为层与层之间的变化维持了激活幅值(向前传播) 和梯度(向后传播)。
其他的一些方法可以减轻学习过程中层于层之间的差异。例如利用二阶信息来为每个参数分别设置学习速率。例如,我们可以hessian矩阵的对角线元素或者梯度方差估计这样一个学习率。这两种方法都应用在shapeset3*2数据集上,并使用 tanh函数以及标准初始化。在性能上,我们得到了一个收获,但是没有达到从规范化初始化获得的结果。此外,我们获得更深远的收获来自于将规范化初始化与二阶信息结合在一起:估计的hessian矩阵会注重神经元之间的差异,没有将层与层间重要初始差异联系起来。
在所有提到的实验中,我们在每一层都使用了相同数量的神经元。然而,我们证实当我们层的规模增加或者减少时,也得到了相同的收获。
本文研究的其他收获如下:
1、对于研究深度神经网络难训练的问题,在层与层之间观察激活值、梯度、训练迭代次数是一个强有力的调查工具。
2、当初始化的是小的随机权重的时候,sigmod激活函数(非0对称)应该要避免使用,因为在初始阶段顶层隐含层的饱和性下,它们会产生活力不足的学习进程。
3、保持层与层之间的转换,这样会使得激活值和梯度传播的很好,这种方式会很有用,有利于估计纯监督深度神经网络和无监督预训练之间的大部分差异。
4、还有很多我们的发现让然是很奇怪的,建议为来的调查研究能够更好的理解深度神经网络的梯度与训练动态过程。
以上便是《Understanding the difficulty of training deep deedforward neural networks 》的第三部分解读。
写在后面的话,整篇论文,作者用清晰的行文思路,严谨的逻辑推理,实事求是的实验结果,环环相扣,“步步惊心”,向我们展示了深度学习、深度神经网络中更为细节的一面,让我们领略到其中的魅力,令深度学习人“心驰神往”。细细品读该文,可以帮助我们更好地理解深度神经网络,同时也让我们在研究深度学习时有理可循,借鉴 bengio的科学研究方法,也让我们少走弯路。站在巨人的肩膀上,你会看的更远。谢谢!
❈
全球人工智能近期经典文章推荐
干货|如何利用 TensorFlow 创建第一个神经网络
深度学习里数学之--方差--美妙而富有韵味
备受争议的 D-Wave新型量子计算机 竟然找到了第一个买家
干获|详解深度学习框架——TensorFlow
首届“人工智能奥运会“ 阿里巴巴拿下奥运会TOP赞助商
如何优雅地 对深度神经网络 进行训练
Google|“自动机器学习”取得重大突破:机器设计的机器学习软件已达AI专家设计水平!
【南大教授】提出“超深度学习”欲颠覆“深度学习”,你怎么看?
❈