排序演化（二）：归并

归并排序

灵感

记得在军训的时候，队伍都是四排的

每排都是有序的，我们这里就默认左低右高。

训练四排，当我们转移目的地的时候，为了避免霸占道路，我们就会变成一列纵队

我们当时的教官是怎么快速让四排变成一列的呢？

1. 教官先走到我们的左边
2. 喊 向左转，此时我们就变成了四列纵队朝着教官了
3. 教官比较一下四列队伍的前面第一个人（共四人），比较四人的身高
4. 挑出最矮的，站在一个新的地方排成一列纵队
5. 不断重复比较四列队伍的前面第一个人（共四人)的身高，挑出然后往新的队伍添加

默认原本每排严格身高递增，现实总教官总是目测的，没那么精确

分分钟，四排就变成一列了。

看来这种方式的排序效果很棒呀！我们怎么运用到数组排序中呢？

分割

我们思考下前面方法的前提

• 两队以上的有序队伍

这个前提突然就让我们想到插入排序，我们把第一个元素当成有序队列了。那此时较之前者的，这里多了一个两队以上，那好办呀！我们可以把整个队列里的人，每个人独立为一体，视为一个有序队列。完美！

那用代码怎么实现上面把一列队伍最后切割成一个一个人的呢？

对半切，获得对半后的结果，再对这个结果对半切，直到该结果为一个人。

再对分割后的结果对半切时，这个结果是有左右两半的，所以对结果对半切，要对左右分别对切

let arr = [1, 2, 3, 4]
// 找到中间线，从0到中间线为左，从中间线到尾为右
const middle = arr.length / 2
const left = arr.slice(0, middle)
const right = arr.slice(middle, arr.length)
console.log('left:', left); //left: [ 1, 2 ]
console.log('right:', right); //right: [ 3, 4 ]

为了达到有序的效果，我们要不断切，一直切到每个结果只有一个元素为止

function mergeSort(arr) {
  // 切到队列只有一个元素就不继续切
  if (arr.length > 1) {
    // 找到中间线，然后对着中间线一刀切下去
    const middle = Math.floor(arr.length / 2)
    // 对半结果的左边
    const left = mergeSort(arr.slice(0, middle))
    // 对半结果的右边
    const right = mergeSort(middle, arr.length)
    }
  // 此时每个队列只有一人了 停止对半切
  return
}

这里使用了递归，看不懂的话，我也没办法了

合并

前提我们已经完成了。

现在我们要的是模拟教官的合并了。

上面军训的例子，教官是四排归并成一列，我们简单点，使用两排归并成一列

教官每次比较的都是两列总的第一位同学，在编程里我们要有下标来表示了，我们这里需要用到两个变量来表示

let left = [1, 4]
let right = [2, 3]
let i = 0
let j = 0

// 左队第一位
console.log(left[i]); // 1
// 右队第一位
console.log(right[j]); // 2

为什么要使用两个变量呢？因为当我们比较两者后，会让矮的那个人，走到另一个地方新成一队，然后不断往那队伍里添加，那如果走的是左队第一位1，arr[0，那现在的左队第一位就为4，代码表示起来就是arr[1]

let left = [1, 4]
let right = [2, 3]
let i = 0
let j = 0

const ret = []
// 左队第一位
console.log(left[i]); // 1
// 右队第一位
console.log(right[j]); // 2

// 比较
if (left[i] < right[j]) {
  ret.push(left[i])
  i++
} else {
  ret.push(right[j])
  j++
}

// 新队伍
console.log(ret); // [ 1 ]
// 此时，左队第一位
console.log(left[i]); // 4
// 此时，右队第一位
console.log(right[j]); // 2

上面看懂的话，我们就把比较的那段代码写优雅点

ret.push(left[i] < right[j] ? left[i++] : right[j++])

i++在后面，表示先使用left[i]，此时的i还没加一，使用完后再把 i 的值加一，等于

ret.push(left[i])
i++

这个比较后插入的动作，什么时候停止呀?

当其中一个队伍没人的时候，我们就不用比较了！这不是废话吗？

代码表示起来就是，i 或 j 一旦无法表示数组里的数时就停止，即队伍没人的意思

while (i < left.length && j < right.length)

当其中一个队伍没人的时候，另一个队伍剩很多人怎么办呢？

直接走到新队伍后面呀！

这四人绝对比新队伍里的任何一个人都高！而且这四人还是有序的。

如果想不明白的话，你思考下

当左队还剩一个人的时候

此时右队有四个人

左队第一位和右队第一位比，

左队第一位矮，遂走到新队伍后面（即，新队伍中最高者）

右队是有序递增的，第一位已经比新队伍中最高者高了（刚刚比过了呀）

那整个右队当然是比新队伍都高的。

那直接走到新队伍后面就可以了呀！

这用代码怎么表示呢？

我们可以使用 concat

let ret = [1, 2, 3]
let right = [4, 5, 6]
console.log(ret.concat(right));
//[ 1, 2, 3, 4, 5, 6 ]

然后我们再思考一个点

如果左队为空了，那么右队一定还有人

右队为空了，那么左队一定还有人

为什么呢？

当左右队都只有一个人的时候

经过比较，就矮的那个就会离开

那此时，高的那个还在原队伍中呀！

再综合前面说的剩余多人的情况时，直接添加到新队伍后面

使用 slice来表示剩余的人

let arr = [1, 2, 3, 4]
let j = 2
console.log(arr[j]); // 3
console.log(arr.slice(j)); //[ 3, 4 ]

结合前面说的就有下面这段代码

ret.concat(i < left.length ? left.slice(i) : right.slice(j))

最后就有

let left = [1, 3, 5]
let right = [2, 4, 6, 8, 10]
function merge(left, right) {
  let i = 0
  let j = 0
  const ret = []
  // 表示一旦其中一个队伍没人 就停止
  while (i < left.length && j < right.length) {
    ret.push(left[i] < right[j] ? left[i++] : right[j++])
  }
  return ret.concat(i < left.length ? left.slice(i) : right.slice(j))
}
console.log(merge(left, right));
// [ 1, 2, 3, 4, 5, 6, 8, 10 ]

递归

现在我们分割和合并都完成了

分割

function mergeSort(arr) {
  if (arr.length > 1) {
    const middle = Math.floor(arr.length / 2)
    const left = mergeSort(arr.slice(0, middle))
    const right = mergeSort(arr.slice(middle, arr.length))
    }
  return
}

合并

function merge(left, right) {
  let i = 0
  let j = 0
  const ret = []
  while (i < left.length && j < right.length) {
    ret.push(left[i] < right[j] ? left[i++] : right[j++])
  }
  return ret.concat(i < left.length ? left.slice(i) : right.slice(j))
}

两者要怎么结合呢？

我们只要在分割代码中添加合并函数就可以了

function mergeSort(arr) {
  if (arr.length > 1) {
    const middle = Math.floor(arr.length / 2)
    const left = mergeSort(arr.slice(0, middle))
    const right = mergeSort(arr.slice(middle, arr.length))
+		arr = merge(left,right)    
    }
  return
}

一个归并排序就出来啦

function mergeSort(arr) {
  if (arr.length > 1) {
    const middle = Math.floor(arr.length / 2)
    const left = mergeSort(arr.slice(0, middle))
    const right = mergeSort(arr.slice(middle, arr.length))
    arr = merge(left, right)
  }
  return arr
}

function merge(left, right) {
  let i = 0
  let j = 0
  const ret = []

  while (i < left.length && j < right.length) {
    ret.push(left[i] < right[j] ? left[i++] : right[j++])
  }
  return ret.concat(i < left.length ? left.slice(i) : right.slice(j))
}

let arr = [8, 7, 6, 5, 4, 3, 2, 1]
console.log(mergeSort(arr));
// [ 1, 2, 3, 4, 5, 6, 7, 8 ]

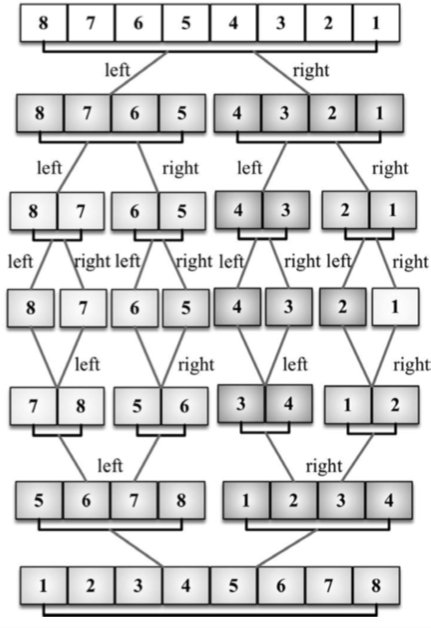
我们添加的

    const left = mergeSort(arr.slice(0, middle))
    const right = mergeSort(arr.slice(middle, arr.length))
+		arr = merge(left,right)    

是在两个递归的后面，所以只有递归终结的时候，方才执行，此时left和right都表示一个数，把只有一个数的left和right合并成一组后，作为arr返回，而这个arr成了另一个函数里的left，另一边的right也是如此。

再不懂就自己看图吧。

效率

空间效率

如果要算空间效率的话，我们上面的归并排序写法就有点奢侈和难以说明了.

主要是上面的写法能很清楚的明白归并的思想，上面能明白，此时再来看采用原地归并这种写法，就比较好懂了。

function mergeSort(arr) {
  const arrTemp = []
  sort(arr, arrTemp, 0, arr.length - 1)
  return arr
}

function sort(arr, arrTemp, low, hight) {
  if (hight <= low) return
  // 取中间值，这么写是避免溢出 类似 (low+hight)/2
  let middle = low + Math.floor((hight - low) / 2)
  sort(arr, arrTemp, low, middle)
  sort(arr, arrTemp, middle + 1, hight)
  merge(arr, arrTemp, low, middle, hight)
}

// 将有序的arr[low...midddle]和arr[middle+1...hight]归并
function merge(arr, arrTemp, low, midlle, hight) {
  let i = low
  let j = midlle + 1
  // 将arr[low...hight]复制到arrTemp[low...hihgt]
  // 因为arr[low...hight]是要存储两队归并后的有序结果
  for (let k = low; k <= hight; k++) {
    arrTemp[k] = arr[k]
  }

  for (let k = low; k <= hight; k++) {
    if (i > midlle) arr[k] = arrTemp[j++]
    else if (j > hight) arr[k] = arrTemp[i++]
    else if (arrTemp[j] < arrTemp[i]) arr[k] = arrTemp[j++]
    else arr[k] = arrTemp[i++]
  }
}

let arr = [11, 2, 33, 4, 55, 6]
console.log(mergeSort(arr));
// [ 2, 4, 6, 11, 33, 55 ]

这里我就点一下第22行的四种判断表示的意思，能看懂就看懂了，看不懂的，到时自己去翻《算法》这本书吧

1. 左半边用尽(取右半边的元素)
2. 右半边用尽(取左半边的元素)
3. 右半边的当前元素小于左半边的当前元素(取右半边的元素)
4. 右半边的当前元素大于等于左半边的当前元素(取左半边的元素)

那上面空间上，我们就要创建了一个和arr等长的数组arrTemp 作为中间站。

那就很容易看出，归并排序有个负作用，即需要额外的空间且与数组长度成正比，约一约，就是

时间效率

归并排序在最坏情况下的比较次数和任意基于比较的排序算法所需的最少比较次数都是，这里指是普通的归并，其实归并很有很多细节可以优化

略略的写，没太多时间深入。

稳定性

当相等的元素是无法分辨的，比如像是整数，稳定性并不是一个问题。然而，假设以下的数对将要以他们的第一个数字来排序。

(4,1)(3,1)(3,7)(5,6)

在这个状况下，有可能产生两种不同的结果，一个是让相等键值的纪录维持相对的次序，而另外一个则没有：

(3,1)(3,7)(4,1)(5,6)（維持次序）

(3,7)(3,1)(4,1)(5,6)（次序被改變）

不稳定排序算法可能会在相等的键值中改变纪录的相对次序，但是稳定排序算法从来不会如此。不稳定排序算法可以被特别地实现为稳定。作这件事情的一个方式是人工扩展键值的比较，如此在其他方面相同键值的两个对象间之比较，（比如上面的比较中加入第二个标准：第二个键值的大小）就会被决定使用在原先数据次序中的条目，当作一个同分决赛。然而，要记住这种次序通常牵涉到额外的空间负担。

归并排序是稳定的，后面要讲的 快速排序是不稳定的