一. 概述
由于RSA、AES等国际算法面临高强度算法禁售和被部署后门风险,我国基于ECC椭圆曲线,自研SM2/SM3/SM4/SM9一套安全算法。根据国家整体战略,金融及重要领域要逐步实现国密算法替换,另根据人民银行总体规划,在2022年金融行业要全面应用国密算法。
在FireFly移动金融开发平台中,完善的提供了支持国密算法的加解密算法包。为了更好的使用和推广国密算法,下面具体分析ECC椭圆曲线的加密原理。

二. 椭圆曲线算法原理
椭圆曲线(Elliptic Curve Cryptography)加密算法是一种公钥加密技术,以椭圆曲线理论为基础。利用有限域上椭圆曲线的点构成的Abel群离散对数难解性,实现加密、解密和数字签名。将椭圆曲线中的加法运算与离散对数中的模乘运算相对应,就可以建立基于椭圆曲线的对应密码体制。

三. 椭圆曲线算法优势
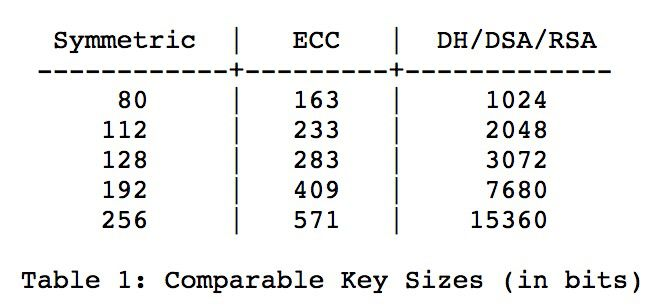
1. 更适合于移动互联网
在同等加密安全强度下,ECC密钥长度为163bit,而RSA密钥长度为1024bit。ECC加密算法的密钥长度很短,意味着占用更少的存储空间,更低的CPU开销和占用更少的带宽。随着越来越多的用户使用移动设备来完成各种网上活动,ECC加密算法为移动互联网安全提供更好的客户体验。
2. 更好的安全性
ECC加密算法提供更强的保护,比目前的其他加密算法能更好的防止攻击,使你的网站和基础设施比用传统的加密方法更安全,为移动互联网安全提供更好的保障。
3. 更好的性能
ECC加密算法需要较短的密钥长度来提供更好的安全。

四.椭圆曲线理论基础
1. 定义
一条椭圆曲线是在射影平面上满足方程
Y2Z + a1XYZ + a3Yz2 = X3+ a2X2Z + a4XZ2 + a5Z3
所有点的集合,且曲线上的每个点都是非奇异(或光滑)的。
该方程是Weierstrass方程,是一个齐次方程。
椭圆曲线的形状,并不是椭圆的。只是因为椭圆曲线的描述方程,类似于计算一个椭圆周长的方程,故得名。下面是椭圆曲线的形状:
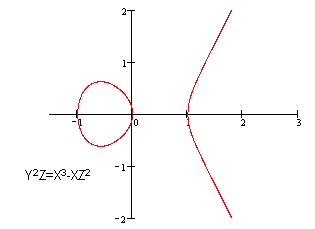
由椭圆曲线的定义可以知道,椭圆曲线是光滑的,所以椭圆曲线上的平常点都有切线。
2. 椭圆曲线上的加法
① 运算法则
任意取椭圆曲线上两点P、Q (若P、Q两点重合,则做P点的切线)做直线交于椭圆曲线的另一点R’,过R’做y轴的平行线交于R。我们规定P+Q=R。(如图)
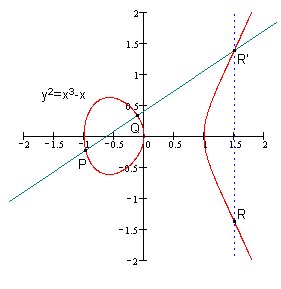
② 运算法则详解
这里的+是从普通加法中抽象出来的加法,他具备普通加法的一些性质,但具体的运算法则显然与普通加法不同。
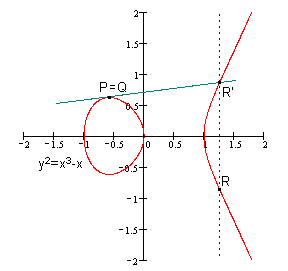
k个相同的点P相加,我们记作kP。如下图:P+P+P = 2P+P = 3P,3P即为P点的3倍点。
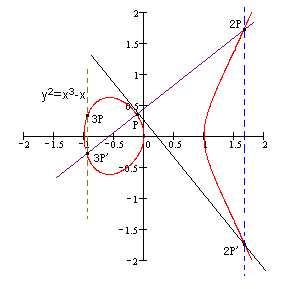
3. 有限域上的椭圆曲线
① 有限域
前面讲到的椭圆曲线是定义在实数域上的,实数是连续的,导致了椭圆曲线的连续,但是并不适合用于加密。所以,必须把椭圆曲线变成离散的点,需要把椭圆曲线定义在有限域上(顾名思义,有限域是一种只有由有限个元素组成的域)。
下面,给出一个有限域Fp,这个域只有有限个元素。
Fp中只有p(p为素数)个元素0,1,2 …… p-2,p-1;
Fp 的加法(a+b)法则是a+b≡c (mod p);即(a+b)÷p的余数和c÷p的余数相同。
Fp 的乘法(a×b)法则是 a×b≡c (mod p);
Fp 的除法(a÷b)法则是 a/b≡c (mod p);即a×b-1≡c (mod p);(b-1也是一个0到p-1之间的整数,但满足b×b-1≡1 (mod p);
Fp 的单位元是1,零元是0。
② 可加密椭圆曲线
同时,并不是所有的椭圆曲线都适合加密。y2 = x3 + ax + b是一类可以用来加密的椭圆曲线,也是最为简单的一类。下面就把 y2 = x3 + ax + b这条曲线定义在Fp上:
选择两个满足下列条件的小于p(p为素数)的非负整数a、b
4a3 + 27b2 ≠ 0 (mod p)
则满足下列方程的所有点(x,y),再加上无穷远点O∞ ,构成一条椭圆曲线。
y2 = x3 + ax + b(mod p)
其中x,y属于0到p-1间的整数,并将这条椭圆曲线记为Ep(a,b)。
示例:查看 y2 = x3 + x + 1 (mod 23)的图像
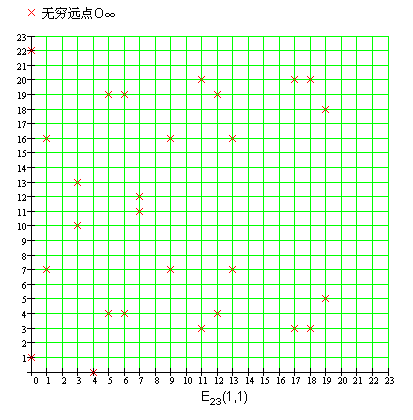
这样椭圆曲线,就成了一个一个离散的点,椭圆曲线在不同的数域中会呈现出不同的样子,但其本质仍是一条椭圆曲线。
③ 计算椭圆曲线上点的坐标
Fp上的椭圆曲线同样有加法,根据加法法则,可以计算出椭圆曲线上点的坐标。
已知点P(x1, y1), Q(x2,y2),计算点R(x3, y3):
X3 ≡ k2 – x1 – y1 (mod p)
Y3 ≡ k(x1–x3) –y1 (mod p)
若P≠Q,PQR三点共线,其斜率 k=(y2–y1) / (x2 –x1) 。
其中若P=Q,PR为过P点的椭圆切线,其斜率 k=(3x12+ a) / 2y1
④ 椭圆曲线上的点的阶
如果椭圆曲线上一点P,存在最小的正整数n,使得数乘nP=O∞,则将n称为P的阶,若n不存在,我们说P是无限阶的。事实上,在有限域上定义的椭圆曲线上所有的点的阶n都是存在的。

五. 椭圆曲线加解密原理
1. 加解密依据
公开密钥算法总是要基于一个数学上的难题。比如RSA依据的是:给定两个素数p、q 很容易相乘得到n,而对n进行因式分解却相对困难。那椭圆曲线上有什么难题呢?
考虑如下等式:
K=kG [其中K,G为Ep(a,b)上的点,k为小于n(n是点G的阶)的整数]
给定k和G,根据加法法则,计算K很容易;但给定K和G,求k就相对困难了。这就是椭圆曲线加密算法采用的难题。
我们把点G称为基点(base point),k(k<n,n为基点G的阶)称为私有密钥(privte key),K称为公开密钥(public key)。
k = 2,K为G的2倍点;
k = 3,K为G的3倍点;
k = 4,K为G的4倍点;
...
如果给定椭圆曲线上K为G的一个倍点,如何计算K为G的多少倍?直观上理解,正向计算一个倍点是容易的,反向计算一个点K是G的几倍点则困难的多。因此在椭圆曲线算法中,将倍数k做为私钥,将K做为公钥。
2. 加解密过程
现在我们描述一个利用椭圆曲线进行加密通信的过程:
用户A选定一条椭圆曲线Ep(a,b),并取椭圆曲线上一点,作为基点G。
用户A选择一个私有密钥k,并生成公开密钥K=kG。
用户A将Ep(a,b)和点K,G传给用户B。
用户B接到信息后,将待传输的明文编码到Ep(a,b)上一点M(编码方法很多,这里不作讨论),并产生一个随机整数r(r<n)。
用户B计算点C1=M+rK;C2=rG。
用户B将C1、C2传给用户A。
用户A接到信息后,计算C1-kC2,结果就是点M。因为
C1-kC2=M+rK-k(rG)=M+rK-r(kG)=M
再对点M进行解码就可以得到明文。
在这个加密通信中,如果有一个偷窥者H ,他只能看到Ep(a,b)、K、G、C1、C2而通过K、G 求k 或通过C2、G求r 都是相对困难的。因此,H无法得到A、B间传送的明文信息。
3. 加解密参数
密码学中,描述一条Fp上的椭圆曲线,常用到六个参数:
T=(p,a,b,G,n,h)。
p 、a 、b 用来确定一条椭圆曲线,
G为基点,
n为点G的阶,
h 是椭圆曲线上所有点的个数m与n相除的整数部分。
这几个参数取值的选择,直接影响了加密的安全性。参数值一般要求满足以下几个条件:
p 当然越大越安全,但越大,计算速度会变慢,200位左右可以满足一般安全要求;
p≠n×h;
pt≠1 (mod n),1≤t<20;
4a3 + 27b2 ≠ 0 (mod p);
n 为素数;
h≤4。

六.椭圆曲线数字签名原理(ECDSA)
1. 概述
椭圆曲线数字签名算法(ECDSA)是使用椭圆曲线密码(ECC)对数字签名算法(DSA)的模拟。
ECDSA是ECC与DSA的结合,整个签名过程与DSA类似,所不一样的是签名中采取的算法为ECC,最后签名出来的值也是分为r,s。
2. 签名过程
选择一条椭圆曲线Ep(a,b),和基点G;
选择私有密钥k(k<n,n为G的阶),利用基点G计算公开密钥K=kG;
产生一个随机整数r(r<n),计算点R=rG;
将原数据和点R的坐标值x,y作为参数,计算SHA1做为hash,即Hash=SHA1(原数据,x,y);
计算s≡r - Hash * k (mod n);
r和s做为签名值,如果r和s其中一个为0,重新从第3步开始执行。
3. 验签过程
接受方在收到消息(m)和签名值(r,s)后,进行以下运算:
计算:sG+H(m)P=(x1,y1), r1≡x1 mod p。
验证等式:r1 ≡r mod p。
如果等式成立,接受签名,否则签名无效。

七.椭圆曲线算法应用
椭圆加密算法的应用范围很广,如 TLS、openPGP以及SSH都在使用,在比特币以及其他加密数字货币中也得到广泛使用。另外我国重点推广的国密SM2算法也正是基于椭圆曲线算法。下面以SM2和TLS为例进行说明:
1. SM2
① 概述
SM2算法和RSA算法都是公钥密码算法,随着密码技术和计算技术的发展,目前常用的1024位RSA算法面临严重的安全威胁,我们国家密码管理部门经过研究,决定采用SM2椭圆曲线算法替换RSA算法。SM2算法在安全性、性能上都具有优势,参见表1算法攻破时间,表2算法性能。
RSA密钥强度 | 椭圆曲线密钥强度 | 是否攻破 |
512 | 106 | 已被攻破 |
768 | 132 | 已被攻破 |
1024 | 160 | |
2048 | 210 |
表1 算法攻破时间
算法 | 签名速度(次/秒) | 验签速度(次/秒) |
1024位RSA | 2792 | 51224 |
2048位RSA | 455 | 15122 |
256位SM2 | 4095 | 871 |
表2 算法性能
② SM2和椭圆曲线算法之间的关系
SM2算法采用的椭圆曲线方程为:y2= x3+ ax + b,在SM2算法标准中,通过指定a、b系数,确定了唯一的标准曲线。同时,为了将曲线映射为加密算法,SM2标准中还确定了其它参数,供算法程序使用。
③ SM2加解密过程
下面是SM2加解密流程中使用到的符号缩略语:
A, B 使用公钥密码系统的两个用户。
dB 用户B 的私钥。
E(Fq) Fq 上椭圆曲线E 的所有有理点(包括无穷远点O)组成的集合。
Fq 包含q 个元素的有限域。
G 椭圆曲线的一个基点,其阶为素数。
Hash() 密码杂凑算法。
Hv( ) 消息摘要长度为v 比特的密码杂凑算法。
KDF( ) 密钥派生函数。
h 余因子,h=#E(Fq)/n,其中n 是基点G 的阶。
M 待加密的消息。
M’ 解密得到的消息。
n 基点G 的阶(n 是#E(Fq)的素因子)。
O 椭圆曲线上的一个特殊点,称为无穷远点或零点,是椭圆曲线加法群的单位元。
PB 用户B 的公钥。
q 有限域Fq 中元素的数目。
a, b Fq 中的元素,它们定义Fq 上的一条椭圆曲线E。
x||y x 与y 的拼接,x、y 是比特串或字节串。
[k]P 椭圆曲线上点P 的k 倍点。
E(Fq) E(Fq)上点的数目,称为椭圆曲线E(Fq)的阶。
M⊕t xor运算
a. 加密算法流程
SM2加密使用公钥加密,公钥由一个曲线坐标点组成,在X.509证书中的公钥表示为04标记开始的2个32byte的BigInteger,即曲线点P(x,y)。SM2公钥加密算法比RSA相对复杂,加密结果由3个部分组成,SM2加密过程中使用了随机数,因此同样的明文数据每一次加密结果都不一样。
设需要发送的消息为比特串M,klen 为M 的比特长度。
为了对明文M 进行加密,作为加密者的用户A 应实现以下运算步骤:
A1:用随机数发生器产生随机数k∈[1, n-1];
A2:计算椭圆曲线点C1 = [k]G=(x1, y1),按SM2 椭圆曲线公钥密码算法第1 部分3.2.9 和3.2.5 给
出的方法,将C1 的数据类型转换为比特串;
A3:计算椭圆曲线点S= [h]PB,若S 是无穷远点,则报错并退出;
A4:计算椭圆曲线点[k]PB=(x2, y2),按SM2 椭圆曲线公钥密码算法第1 部分3.2.6 和3.2.5 给出的
方法,将坐标x2、y2 的数据类型转换为比特串;
A5:计算t = KDF(x2||y2,klen),若t 为全0 比特串,则返回A1;
A6:计算C2=M⊕t;
A7:计算C3= Hash (x2||M|| y2);
A8:输出密文C=C1||C3||C2。
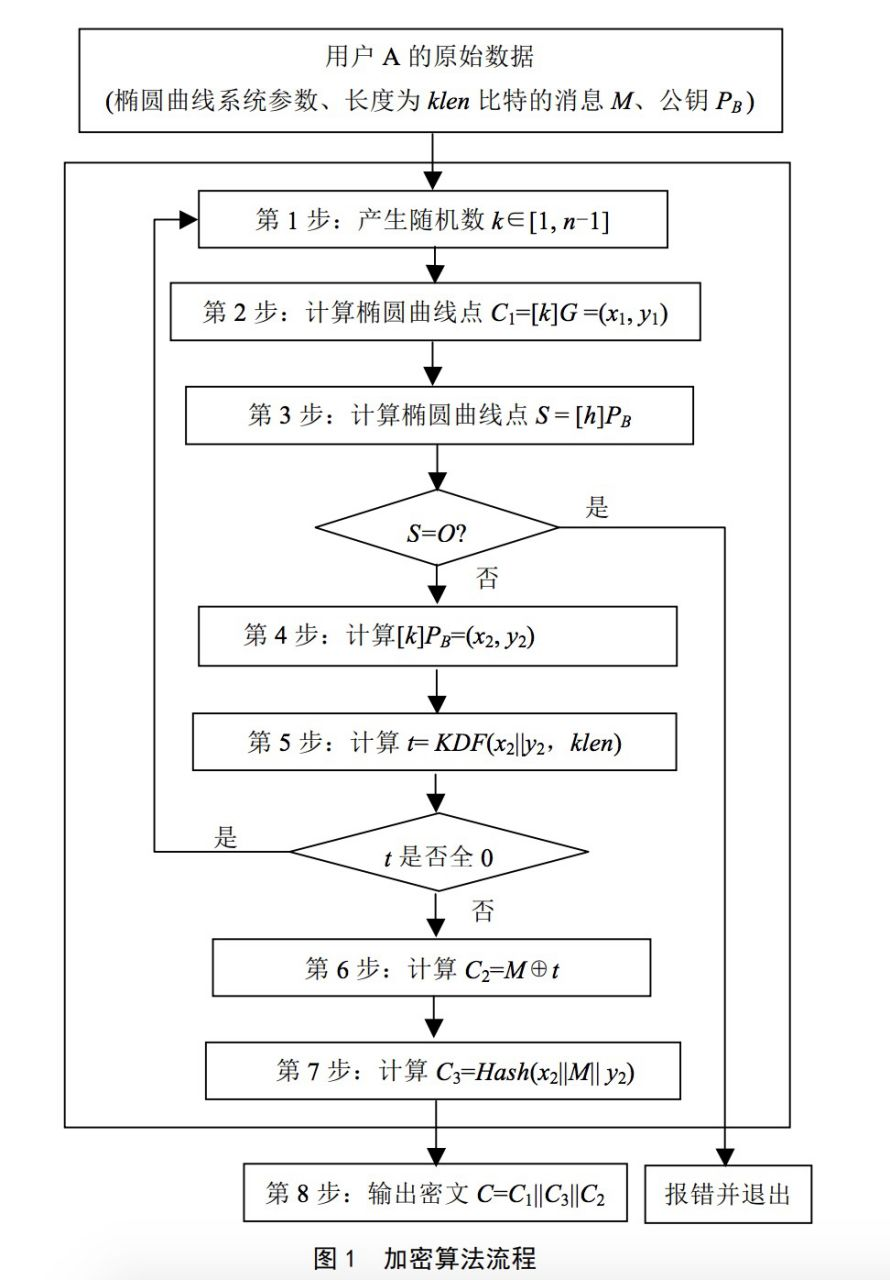
根据国密推荐的SM2椭圆曲线公钥密码算法,首先产生随机数计算出曲线点C1,2个32byte的BigInteger大数,即为SM2加密结果的第1部分。第2部分则是真正的密文,是对明文的加密结果,长度和明文一样。第3部分是杂凑值,用来效验数据。按国密推荐的256位椭圆曲线,明文加密结果比原长度会大96byte。
b. 解密算法流程
SM2解密算法是加密逆运算。首先需要从密文中取出加密结果的3部分值,然后通过私钥计算出M’明文值,最后效验数据
设klen 为密文中C2 的比特长度。
为了对密文C=C1||C3||C2 进行解密,作为解密者的用户B 应实现以下运算步骤:
B1:从C 中取出比特串C1,按SM2 椭圆曲线公钥密码算法第1 部分3.2.4 和3.2.10 给出的方法,
将C1 的数据类型转换为椭圆曲线上的点,验证C1 是否满足椭圆曲线方程,若不满足则报错
并退出;
B2:计算椭圆曲线点S= [h]C1,若S 是无穷远点,则报错并退出;
B3:计算[dB]C1= (x2, y2),按SM2 椭圆曲线公钥密码算法第1 部分3.2.6 和3.2.5 给出的方法,将
坐标x2、y2 的数据类型转换为比特串;
B4:计算t = KDF(x2||y2,klen),若t 为全0 比特串,则报错并退出;
B5:从C 中取出比特串C2,计算M’=C2⊕t;
B6:计算u = Hash (x2||M’|| y2),从C 中取出比特串C3,若u≠C3,则报错并退出;
B7:输出明文M’。
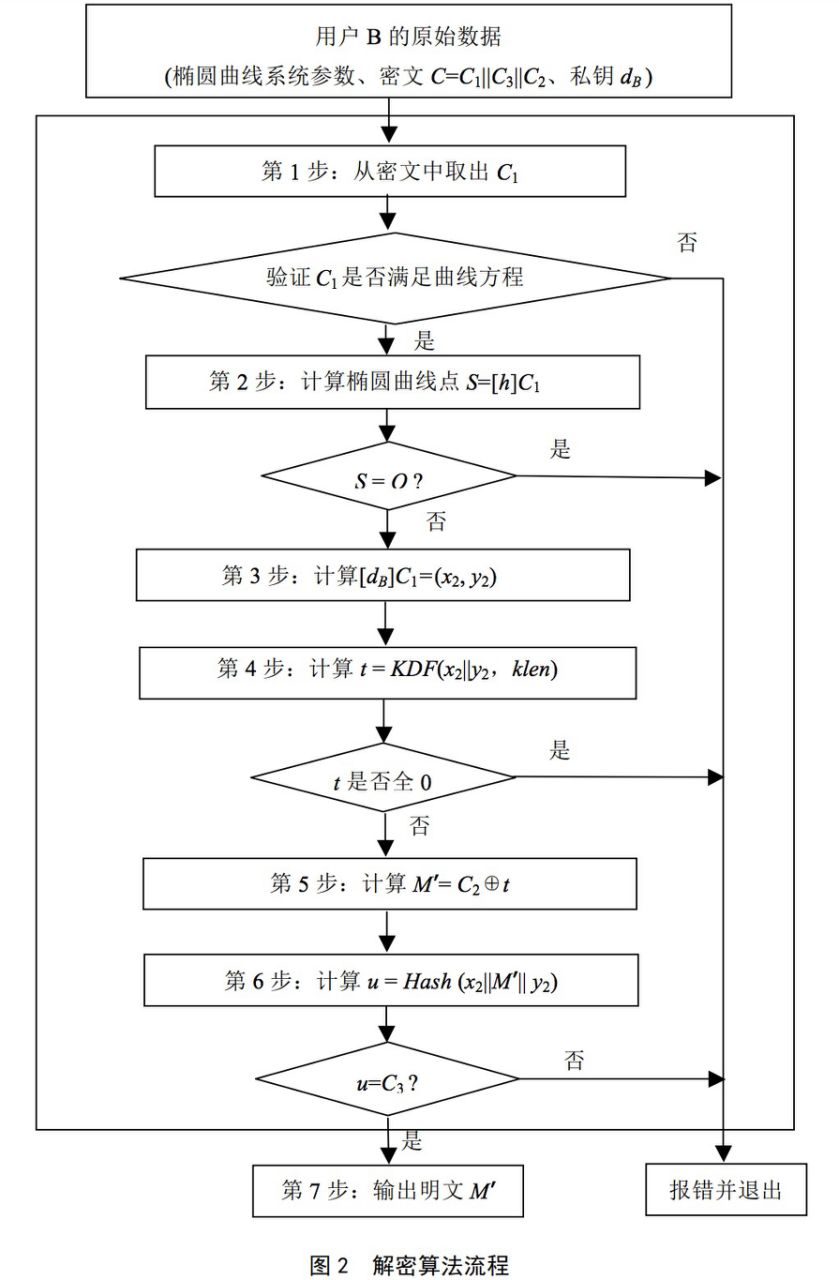
SM2解密同样也可以使用软算法实现。但因为涉及到私钥运算,为保护私钥安全,建议在硬件设备中运行,例如UKey等存储介质这样可以更好的保护密钥安全。拿文件加密来说,首先拿UKey里面的加密证书加密,这部分可在应用系统内完成。解密的话则需要加密证书对应UKey才能做解密,由应用系统调用UKey解密接口,在物理硬件内完成数据解密,同时可以受设备PIN码保护。
④ SM2算法的速度和结果长度
简单讲,SM2签名速度快,验签速度慢,这点和RSA算法的特性正好相反。参见上表2。另外,加解密速度和验签速度相当。
SM2支持近128G字节数据长度,加密结果增加96个字节。
SM2签名算法对原始数据量长度无限制,签名结果为64字节。
2. TLS
① 概述
HTTPS 通过TLS 层和证书机制提供了内容加密、身份认证和数据完整性三大功能,可以有效防止数据被监听或篡改,还能抵御MITM(中间人)攻击。TLS 在实施加密过程中,需要用到非对称密钥交换和对称内容加密两大算法。对称内容加密强度非常高,加解密速度也很快,只是无法安全地生成和保管密钥。在TLS 协议中,应用数据都是经过对称加密后传输的,传输中所使用的对称密钥,则是在握手阶段通过非对称密钥交换而来。
② TLS中密钥交换算法
目前最常用的密钥交换算法有RSA 和ECDHE:RSA 历史悠久,支持度好,但不支持PFS(Perfect Forward Secrecy);而ECDHE 是使用了ECC(椭圆曲线)的DH(Diffie-Hellman)算法,计算速度快,支持PFS。
③ 基于ECC的密钥交换算法
下面是五种常见的基于ECC的TLS 密钥交换算法,它们分别模仿DH_DSS,DHE_DSS,DH_RSA,DHE_RSA和DH_anon。

以ECDHE_ECDSA为例:
证书包含ECDSA-capable 公钥,使用ECDHE 算法协商预备主密钥; 证书必须允许密钥用于使用将在Server 密钥交换消息中使用的散列算法进行签名;公钥必须使用一个能够被Client 支持的曲线和点格式,Client 通过Client Hello 消息中的ec_point_formats 扩展指定支持的命名曲线,正如 [TLSECC] 中描述的那样。这是TLS 1.2 中最安全,性能最高的密码套件。
④ ECDHE密钥交换的完整握手流程
A: 客户端向服务器发送Client Hello,告知服务器,客户端支持的协议版本、加密套件等信息。
B: a. 服务端收到响应,选择双方都支持的协议、套件,向客户端发送Server Hello,同时服务器也将自己的证书发送到客户端(Certificate)。
b. 服务器利用私钥将客户端随机数、服务器随机数、服务器DH参数签名,生成服务器签名。
C: 服务端向客户端发送服务器DH参数以及服务器签名(Server Key Exchange)。
D: 客户端向服务端发送客户端DH参数(Client Key Exchange)。
之后,客户端利用公钥验证服务器签名,客户端与服务器各自利用服务端DH参数、客户端DH参数生成预主密钥,再通过预主密钥、客户端随机数、服务端随机数生成主密钥(会话密钥)。最后握手完成,所有的消息都通过主密钥加密。如图:


八. 结语
椭圆曲线ECC算法基于椭圆曲线理论,可以用较少的计算能力提供更高的安全强度,有效地解决了“提高安全强度必须增加密钥长度”的工程实现问题,且已经得到广泛的支持和使用,读者在选择加密算法时,ECC算法不失为一个优秀的选择。

九. 参考资料
ECC加密算法入门介绍
https://www.pediy.com/kssd/pediy06/pediy6014.htm
Elliptic Curve Cryptography: a gentle introduction
https://andrea.corbellini.name/2015/05/17/elliptic-curve-cryptography-a-gentle-introduction/
国家密码管理局
http://www.oscca.gov.cn/
国家商用密码(一)SM2椭圆曲线公钥密码算法
http://www.firstsolver.com/wordpress/?p=1938
TLS_ECC
https://tools.ietf.org/html/rfc4492

作者介绍
张冠军 民生科技有限公司 用户体验技术部 Firefly移动金融开发平台工程师
