6591 Another Chess Problem
问题相当于:给定一个棋盘,有一些格子上有障碍物,询问两个格子之间最短路以及方案数。
通过观察可以发现将每一个包含 个格子的正方形空地当作下图的一个蓝色菱形,下图的顶点对应表示棋盘的格子,这样就转化为在下图中计算。
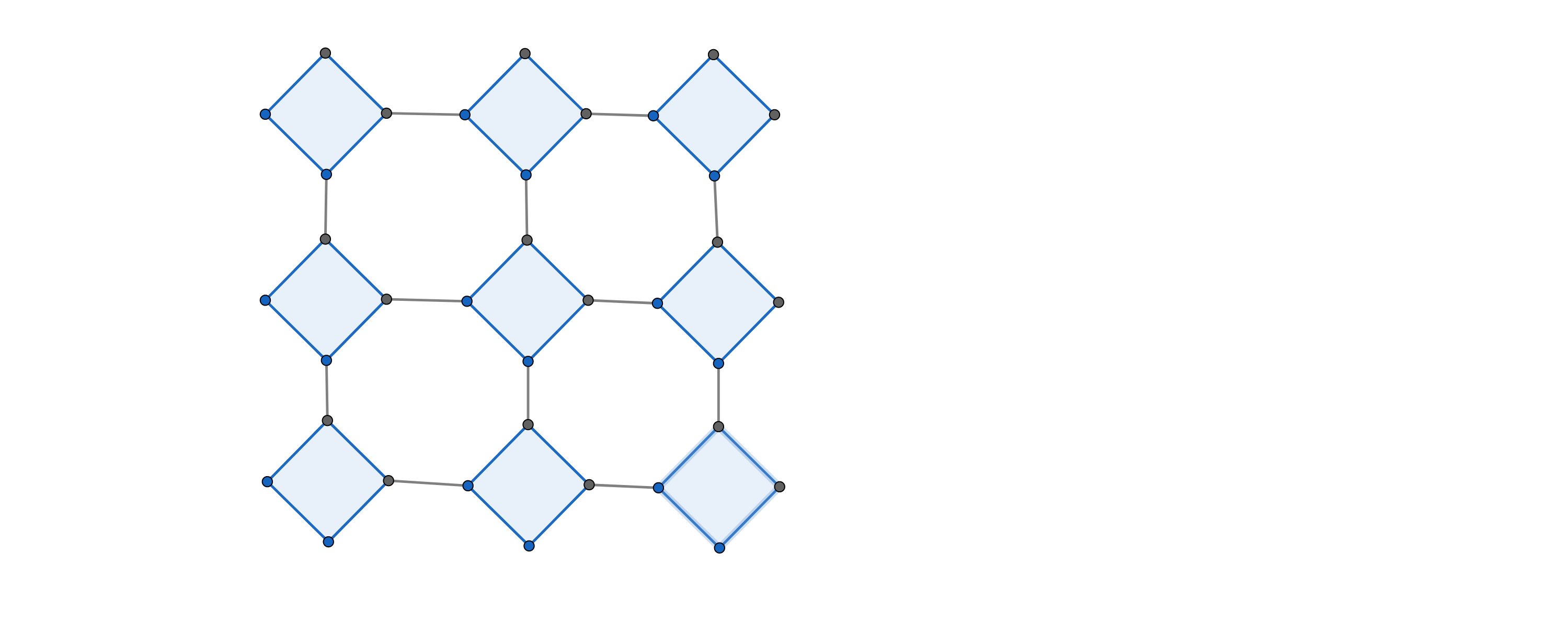
可以先确定询问的两个点在这个图中是哪两个块,然后先考虑块间的移动顺序,可以发现连续走一个方向会比转方向多走 ,所以块间移动要使横着和竖着移动尽量错开,然后再考虑到点在块内也有个初始位置,所以可以枚举起点块出去的位置(顶点)和终点块进入的位置(顶点),最短路就是对四种情况取最小值。设每种情况最少连续同一个方向走的次数是
,
。
块间移动的方案数可以用组合计数算出。
6592 Beauty Of Unimodal Sequence
表示
一定取,序列
的最长上升子序列长度。
表示
一定取,序列
的最长单峰子序列长度。
表示
一定取,序列
的最长下降子序列长度。
表示
一定取,序列
的最长单峰子序列长度。
转移式子挺容易想的,留给读者思考。
枚举单峰子序列最高点下标,可以很方便的求出最长单峰子序列长度。
接下来逐位确定字典序最大的子序列。经过仔细观察可以发现,将候选集合按照下标排序之后,它们的值是单调的。利用该性质即可得出字典序最大最小的最长单峰子序列。
6593 Coefficient
6594 Double Tree
首先对第一棵树进行边分治,假设当前我们正在考虑经过中心边 的所有路径,我们不妨把切掉中心边之后所有和
联通的点标成黑色,所有和
联通的点标成白色。
定义黑点 的权值
定义白点 的权值
那么
现在对于边分治的每个联通块,我们需要考虑第二棵树。第二棵树上有些点是白色,有些点是黑色,有些点无色,对于每次修改,我们需要找一个黑点 ,一个白点
使得
最大。
首先我们有一个结论:
对于一棵边权全是正的树,假如这棵树上有一个点集 A 的最长路端点分别是 u, v,另有一个点集 B 的最长路端点分别是 a, b,那么点集 A ∪ B 的最长路端点 ∈ {u, v, a, b}。
因为有修改操作,所以 的值是在动态变化的,我们用四元组
表示
点在时刻
的权值
。对其进行线段树分治,则修改操作就变成了只有加边操作。
6595 Everything Is Generated In Equal Probability
考虑一个长度为 的随机排列(无相同元素),它所含逆序对数量的数学期望为
。因为每对下标对期望的贡献为
,且期望具有可加性。
令 表示传入一个长度为
的随机排列所获得的函数返回值的数学期望。
容易得到: 。
改写为: 。
这样可以 预处理出
。
。
回答每组数据。
时间复杂度 。
6596 Fantastic Magic Cube
一共有 个单位立方体,将每两个不同单位立方体之间连一条边,边权为这两个单位立方体的价值乘积。如果将一个块
切成块
和块
,显然就切断了
与
的联系,获得了它们之间的边权之和,因此无论怎么切,其实答案是一样的。
令 ,
表示第
个单位立方体的价值。
。使用
计算出所有单位立方体值得分布(也就是计算每种值各有多少个)即可解出该式。
6597 Game
这是一个不平等博弈游戏,采用 计算游戏局面,最后计算游戏和的状态。
注意到游戏局面,没有超出 的表示范围;
如果计算出来的数 ,左边的人获胜;
右边的人获胜;
表示后手获胜;注意没有先手获胜的情况;更没有其他情况。
6598 Harmonious Army
对每个士兵建立一个点 ,点
向源点
连一条边,向汇点
连一条边,分别表示选择两种职业,然后就可以先加上所有的贡献,通过两点关系用最小割建模,如下图所示。
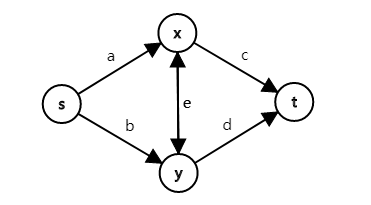
设一条边的三种贡献为 ,可以得到以下方程:
(
都选 Mage)
(
都选 Warrior)
(
选 Mage,
选 Warrior )
(
选 Warrior,
选 Mage )
可得一组解 ,然后将所有有关系的两点的图合并,用所有贡献减掉这个图的最小割即可。
6599 I Love Palindrome String
求出本质不同回文串的数量分布(求每种回文串的个数),然后对每种快速 一下,叠加答案即可;可以用
,后缀自动机,回文自动机,字符串
多种做法实现。
6600 Just Skip The Problem
最优的方案必然是每次询问一个位的具体值,一共有 个二进制位,方案数显然为
。
复杂度 。
6601 Keen On Everything But Triangle
首先考虑区间最大的三个数能否形成三角形,如果不能,考虑区间第二大、第三大、第四大的三个数,以此类推,直到能形成三角形。由三角形最小的两条边大于第三边的性质可知,只需要考虑区间的前 大数即可(最坏情况下区间前几大数形成了斐波那契数列)。
时间复杂度 。
6602 Longest Subarray
如果右端点固定,对于每种元素,可行的左端点下标是两段连续的区间。
(一段出现次数是0,另一段是)
对于每种元素,将它的可行左端点区间在线段树中加一。
当右端点右移的时候,维护 种元素的可行左端点。
查询时只需要询问线段树中最小的、值为 的下标即可。