面试题10:请实现一个函数,输入一个整数,输出该数二进制表示中1的个数。例如把9表示成二进制是1001,有2位是1。因此如果输入9,该函数输出2。
Basic
位运算无外乎 与、或、异或、左移和右移 5 种类型的运算。
使用位运算符进行运算时,整数会自动转为二进制形式,再进行位运算。所有位运算的题型基本都是各种类型位运算的组合。
注意点:整数包含正、负数。
负数右移需要在真空位补上1,如-1,二进制原码为 1000 0001,第一个位为符号位,负数为1,非负数为0开头。在计算机中,负数采用补码来表示,-1的最终二进制表现形式为: 绝对值取反加1,附带上符号位。即 111 1111 加上符号位为 1111 1111。
-1 >> 1 的结果是 1111 1111。
解题思路
判断二进制数中1的位数,可以通过和整数 1 进行 与 运算,1&1 = 1,1&0 = 0。
1 的二进制形式为:0000 0001
9 的二进制形式为:0000 1001
9&1 = 0000 0001 != 0,可以确定最后一位是 1。
那么此时要如何继续往前判断另一个1呢?
解决方案:
将 1 左移一位,即 0000 0001 变为 0000 0010,再判断 9(0000 1001)的第 2 位
0000 0010 & 0000 1001 = 0000 0000 == 0,可以确定第 2 位为 0。
这个过程中,使用一个中间计数器变量 count 每次确定与运算结果为非 0, 则加 1 即可统计 1 的个数。
再将 1 左移一位,即 0000 0010 变为 0000 0100,再判断 9(0000 1001)的第 3 位
0000 0100 & 0000 1001 = 0000 0100 != 0,可以确定第 3 位为 1。
后面同上,1 挨个左移,直到移动到最左边,变成 0000 0000,宣告位遍历结束:
0000 0001
0000 0010
0000 0100
0000 1000
0001 0000
0010 0000
0100 0000
1000 0000
0000 0000 结束
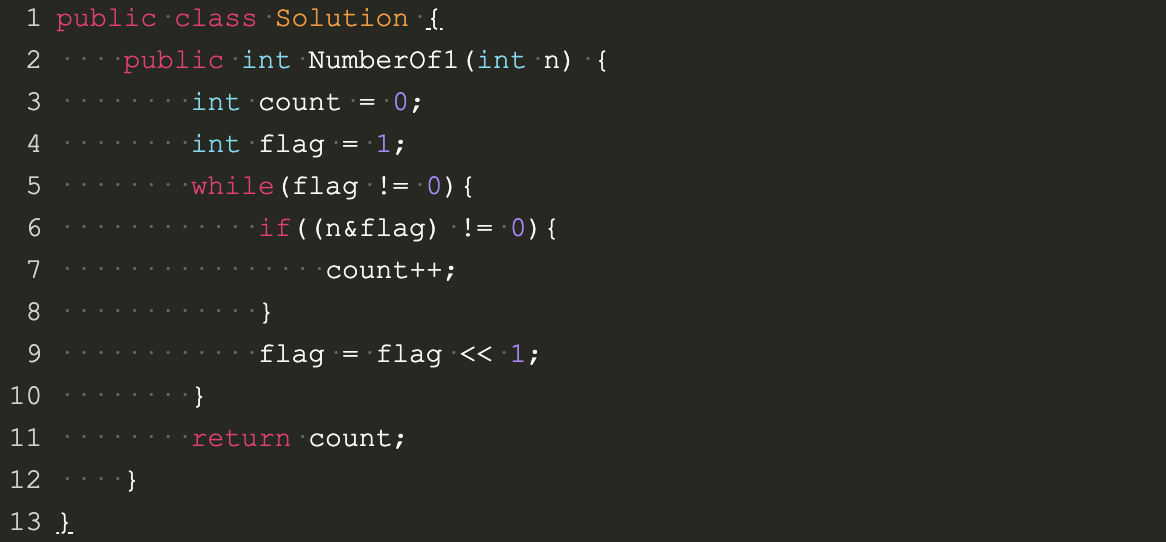
代码实现
public class Solution {
public int NumberOf1(int n) {
int count = 0;
int flag = 1;
while(flag != 0){
if((n&flag) != 0){
count++;
}
flag = flag << 1;
}
return count;
}
}
总结
位运算的题首先要想到位移运算和 与或 运算的结合。
扩展
扩展题目1:用一条语句判断一个整数是不是2的整数次方。
Basic
一个整数如果是2的整数次方,那么它的二进制表示中有且只有一位是1,而其他所有位都是0。
思路分析
方案:把这个整数减去1之后再和它自己做与运算,这个整数中唯一的1就会变成0。
比如 8 的二进制位 0000 1000,0000 1000 - 1 = 0000 1000 - 0000 0001 = 0000 0111
然后再将计算结果和 8 自身进行与运算:0000 1000 & 0000 0111 = 0000 0000 结果刚好是 0 。
代码实现
if((n - 1) & n == 0){
//是2的整数次方
}
扩展题目2:输入两个整数 m 和 n,计算需要改变 m 的二进制表示中的多少位才能得到 n。
比如 10 的二进制表示为 1010,13 的二进制表示为 1101,需要改变 1010 中的 3 位才能得到 1101。
思路分析
我们可以分为两步解决这个问题:第一步求这两个数的异或,第二步统计异或结果中1的位数。
1010 ^ 1101 = 0111
再运用移位运算 + 与运算判断 1 的个数。
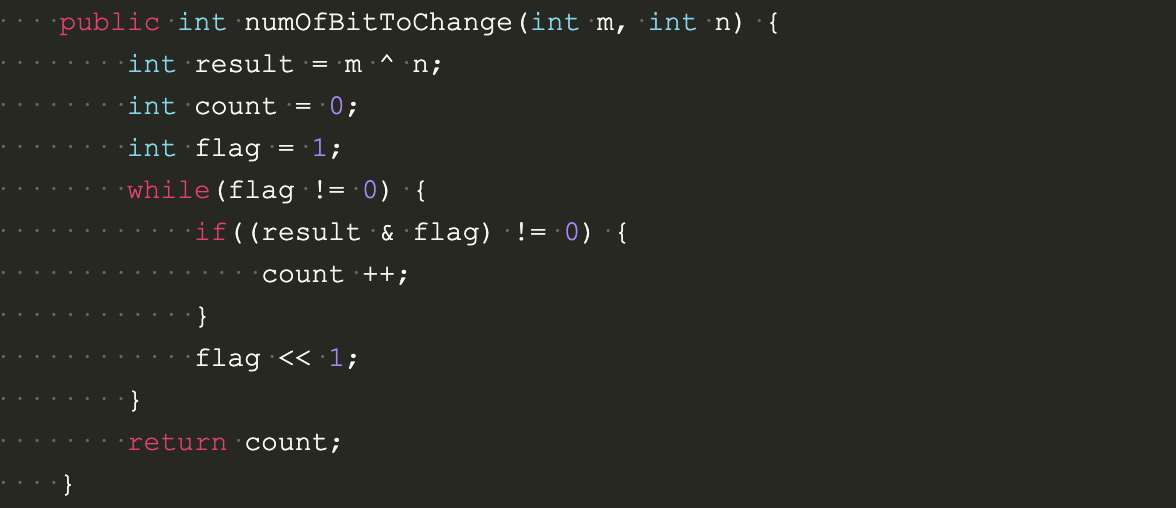
代码实现
public int numOfBitToChange(int m, int n) {
int result = m ^ n;
int count = 0;
int flag = 1;
while(flag != 0) {
if((result & flag) != 0) {
count ++;
}
flag << 1;
}
return count;
}
举一反三
把一个整数减去1之后再和原来的整数做位与运算,得到的结果相当于是把整数的二进制表示中的最右边一个1变成0。
5 - 1 = 0101 - 0001 = 0100
0101 & 0100 = 0100 (最右边的 1 变成0:0101 --> 0100)
4 - 1 = 0100 - 0001 = 0011
0100 & 0011 = 0000 (最右边的 1 变成0:0100 --> 0000)
10 - 1 = 1010 - 0001 = 1001
1010 & 1001 = 1000 (最右边的 1 变成0:1010 --> 1000)
很多二进制的问题都可以用这个思路解决。