面试题6:输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
Basic
前序遍历、中序遍历和后序遍历
- 前序遍历
根-左-右:先访问根节点,再访问左子节点,最后访问右子节点。
- 中序遍历
左-根-右:先访问左子节点,再访问根节点,最后访问右子节点。
- 后序遍历
左-右-根:先访问左子节点,再访问右子节点,最后访问根节点。
总结:前中后序遍历的核心:根节点最先,中间和最后访问。
思路分析
题干:重建一个二叉树,对应返回一个根节点,这个根节点后面的子树就是需要我们去构建的。
Step 1: 首先,需要得到数组中的根节点,由于前序遍历第一个节点就是该二叉树的根节点,所以可以从前序数组中
直接获取 root node。
Step 2: 获取到根节点之后,就可以顺藤摸瓜,去遍历对应的左右子树。由于中序遍历的根节点位于数组中间的某个
位置,根节点的左边数组是左子树,右边数组是右子树。此时就需要根据第一步获取的根节点,从中序数组中,分割出
左右子树所属的两个数组。
由于对子树的遍历,本质上也都是获取下一层的根节点,即第一层的子树的第一个节点,相对于这个子树就是一个根节点,
直到递归到叶子节点这个 base case,叶子结点也相当于一个子树的根节点,只不过它的左右节点都是 null 而已。
因此采用递归解决。根据递归的本质--后进先出的栈--从Base case 叶子节点,挨个返回去构建一个完整的二叉树。
分割数组的示意图如下:
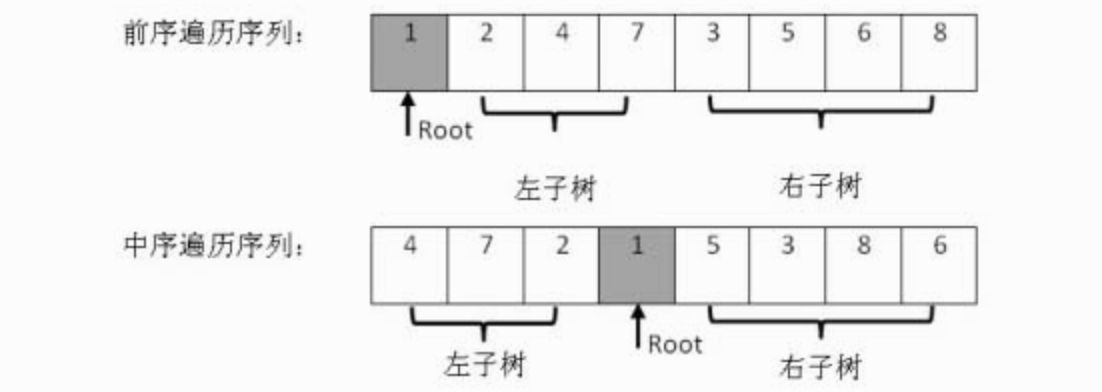
代码实现
/**
* Definition for binary tree
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Solution {
public TreeNode reConstructBinaryTree(int [] pre,int [] in) {
TreeNode root = reConstruct(pre, 0, pre.length - 1, in, 0, in.length - 1);
return root;
}
private TreeNode reConstruct(int[] pre, int preStart, int preEnd, int[] in, int inStart, int inEnd) {
if(preStart > preEnd || inStart > inEnd) {
return null;
}
int rootValue = pre[preStart];
TreeNode root = new TreeNode(rootValue);
for(int i = inStart; i <= inEnd; i ++) {
if(in[i] == rootValue) {
int offSet = i - inStart;
root.left = reConstruct(pre, preStart + 1, preStart + offSet, in, inStart, i - 1);
root.right = reConstruct(pre, preStart + offSet + 1, preEnd, in, i + 1, inEnd);
}
}
return root;
}
}
总结:重构二叉树的场景
可以确定一棵二叉树的两个场景:
-
已知前序和中序遍历
-
已知中序和后序遍历
但是,已知前序和后序遍历,不能确定一棵二叉树。
拓展:根据中序和后序遍历重构二叉树
思路分析
Step 1:同上,根据后序遍历的特点,根节点是最后一个才遍历到的节点,因此我们可以从后序遍历的数组中最后
一个元素得到根节点。
Step 2: 同上,分割左右子树对应的数组。
采用递归解决。
根据递归的本质--后进先出的栈--从Base case 叶子节点,挨个返回去构建一个完整的二叉树。
代码实现
public TreeNode reConstructBinaryTree(int[] in, int[] pos) {
TreeNode root = reConstruct(in, 0, in.length - 1, pos, 0, pos.length - 1);
return root;
}
private TreeNode reConstruct(int[] in, int inStart, int inEnd, int[] pos, int posStart, int posEnd){
if(inStart > inEnd || posStart > posEnd) {
return null;
}
int rootValue = pos[posEnd];
TreeNode root = new TreeNode(rootValue);
for(int i = inStart; i <= inEnd; i++) {
if(in[i] == rootValue){
root.left = reConstruct(in, inStart, i - 1, pos, posStart, posStart + i - inStart);
root.right = reConstruct(in, i + 1, inEnd, pos, posStart + i - inStart + 1, posEnd);
}
}
return toot;
}