晚上朋友发给我一道数学题:
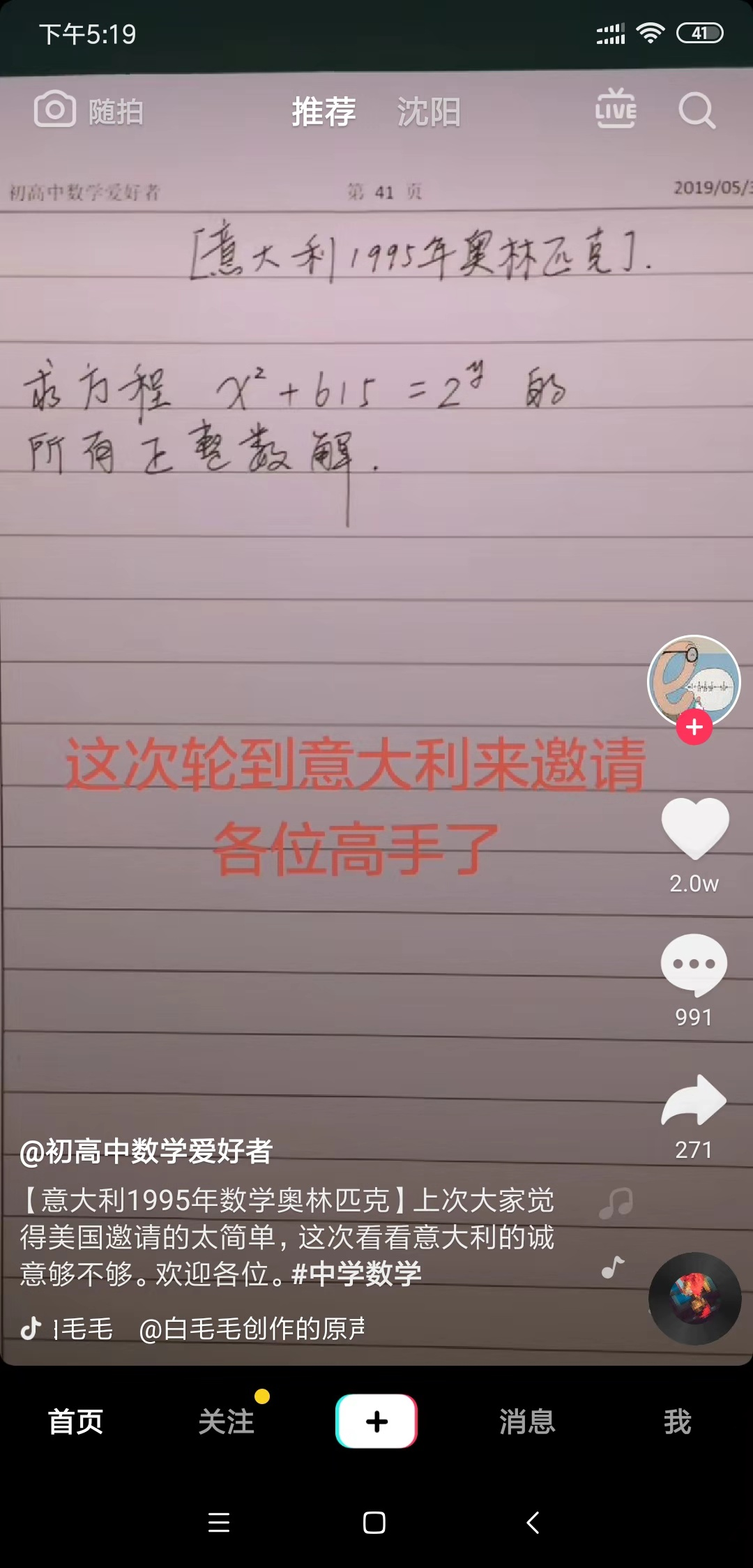
一打眼觉得很有趣,就挑战了一下,这里记录一下过程。
看到此题,我首先的思路是先去找到一个解。
此时我拿出了计算器从 2^y 从小往大开始实验。结果发现
(59, 12)是其中一个解。接着又多试验了几次,其他都是不行的。
然后我就猜测此题的解可能就这一个,当然这也是最后的正确答案。
找到一个解后,我就想去证明解是唯一的。
最初的思路是两个方程做差,
得:
然后想用整除相关理论来论证, x 必须为 59,且 y 必须为 12,但是几番尝试都没有成功。
后来一想 615 这个数应该有特殊价值,不应该把它减掉的。遂修改方程为:
615 是合数,可以做因式分解。615 = 3 * 5 * 41。
如果此时方程右边也能因式分解就好了。
前面的思考,给了我启发,可以使用平方差,但有个前提,y 得为偶数。
假设 y = 2n,z = 2^n 则:
带入 615 的因式分解,会有如下各种情况:
相应的解分别为:
又因为 z = 2^n,即,z 必须为 2 的次幂才行。因此第三个是正确答案 n = 6,x = 59。
推出了正确答案,很欣慰。但是前提条件要求 y 是偶数才行。通过最初的等式,可以推断出 x 必须为奇数(2^y是偶数,615是奇数,因此x^2为奇数,故x为奇数),但是 y 是否一定为偶数呢,我没法推断。
我又开始去尝试假如 y 是奇数的情形,感觉这个有点难,想了一阵子还是没有思路。
此时已经是半夜 1 点了。我的耐心终于耗尽,想看看网上是否有此题解答。bing 一下后竟然发现第一条就是,(Fun Problem: When Does 615 + x^2 = 2^y?)。
它求解的总体思路与我一样,也是平方差因式分解。
但它通过看个位数情况证明出了 y 必须为偶数。用我的话,表达如下:
因为 x 是奇数,它的个位数可能是 1、3、5、7、9。平方后的个位数是 1、9、5、9、1。再加上 615 的个位数 5 后,分别是 6、4、0、4、6。总共可能为 0、4、6三种情况,记为集合 A。
2的y次幂的个位数分别是 2、4、8、6、2、4、8、6...,即 2、4、8、6 这四个数的循环,这四个数记为集合 B。
集合 A 和 B 的交集是 4 和 6。只有当 y 为偶数时,才可能是这两个数。y 必须为偶数证毕。
妙啊!!看完后心想,再给几天时间自己也未必想得到啊!!!
看完下来,是否也觉得此题挺有趣?希望有所帮助。
本文完。