树状数组（更新中）

种树乘凉
606 阅读5分钟

什么是树状数组

树状数组是一种便于进行单点更新和区间查询的数据结构。

注意，这里的更新仅限加减，减法当作加上一个负数来算。
开始，我只会用树状数组来计算前缀和，后来发现只要改变一下getSum中的while循环条件就行了。

模板：

int c[maxn];//树状数组

/* a[x]+=d */
void update(int x,int d)
{
    while(x < maxn)
    {
        c[x] += d;
        x += lowbit(x);
    }
}

/* 统计a数组中前x项的和 */
void getSum(int x)
{
    int sum = 0;
    while(x)
    {
        sum += c[x];
        x -= lowbit(x);
    }
}

解释

下面，我来稍微解释一下上面的代码

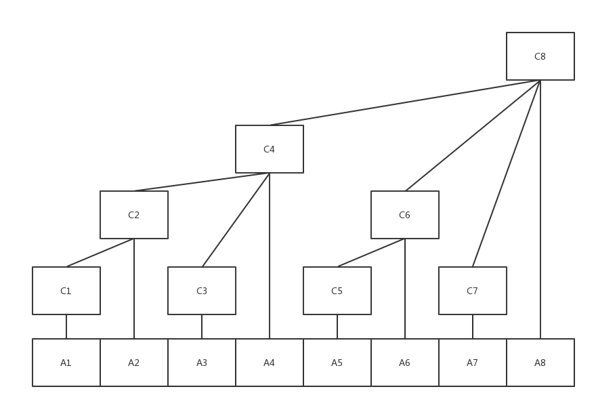
每一项的规律

图中最下面一行是a[]数组，明显可以得出下面的式子

C[1] = C[0001] = A[1];
C[2] = C[0010] = A[1]+A[2];
C[3] = C[0011] = A[3];
C[4] = C[0100] = A[1]+A[2]+A[3]+A[4];
C[5] = C[0101] = A[5];
C[6] = C[0110] = A[5]+A[6];
C[7] = C[0111] = A[7];
C[8] = C[1000] = A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

进一步总结规律就可以得到

下面的k为i的二进制中从最低位到高位连续零的长度。例如i=8(1000)时，k=3;

C[i] = A[i-2^k+1]+A[i-2^k+2]+......A[i]
A[i] = A[i-2^k+2^k]

所以，C[i]由从a[]数组第 i 项起向前数2^k项相加得到。

为了方便求解上面的2^k，我们引入一个lowbit(x) = (x&-x)这个函数。

lowbit函数的原理就不多做解释了，就是利用了正负数补码的特点。
我是通过一个求负数补码的方法来理解 lowbit 函数的。
保留其相应正数的最后一个1，再对左边的所有位取反，然后加上符号位即可。

getSum函数

先解释一下getSum函数
对于(7)_{10} = (0111)_{2}
先初始化sum = 0
第一次循环，sum += C[7] //C[7] = A[7]，lowbit(7) = 1
第二次循环，sum += C[6] //C[6] = A[5]+A[6]，lowbit(6) = 2
第三次循环，sum += C[4] //C[4] = A[1]+A[2+A[3]+A[4]，lowbit(4) = 4

理解个大概就OK了，getSum函数就是把参数x的二进制形式中的每一个1从右到左依次去掉，并在每次去掉之前执行sum+=c[i]，直到lowbit(x) = 0。

下面一小段是补充内容，详细证明一下getSum函数，可以不看
getSum函数实际上利用了，c[i]=\sum_{k=i-lowbit(x)+1}^{i-lowbit(x)+lowbit(x)}a[k]这个公式。
x每一次减掉lowbit(x)之前，sum就加上了对应lowbit(x)项的和。
显然， x 的值就是减掉的所有lowbit(x)的和（因为减到最后是0）。
所以，只需要证明每次加上的lowbit(x)项不会重复就行了。
这一点根据c[i]=\sum_{k=i-lowbit(x)+1}^{i-lowbit(x)+lowbit(x)}a[k]就能看出，因为C[i]包含的最后一项A[i-lowbit(i)+1]和C[i-lowbit(i)]的第一项A[i-lowbit(i)]在A[]中正好是前后关系。

update函数

反过来，该如何update以保证getSum函数的正确性呢？
也就是如果将a[i] += x同步到c[]数组呢，需要改变c[]数组的哪几项呢？

我们直接去看C[j] = A[j-2^k+1]+A[j-2^k+2]+......A[j]这个公式里，会有哪些C[j]包含当前的A[i]即可。
也就是求解 同时满足j-lowbit(j)+1 \leq i 和 j \geq i的 j

///下面先证明如果x满足上面两个式子，那么y = x + lowbit(x)也一定满足
因为lowbit(y) = 2*lowbit(x)，
所以y - lowbit(y) = x + lowbit(x) - 2*lowbit(x) = x - lowbit(x)
并且y >= x，所以只要x满足上面两个式子，那么y也一定满足

接下来的问题就是找到那个最小的 j 就行了，也很简单，就是 i 本身 所以只需要一路执行i += lowbit(i)，就可以保证一个需要更新的C [j]都不会漏掉。
你可能已经发现了，这样下去到什么时候是个头啊。没错，计算的无穷大虽然是正确的，但对于我们做题来说毫无意义，并且C++的数据类型也不允许我们存这么大、这么多。所以，我们自己设置一个足够大（可以应付所有查询）并且合适（不要过大，考虑C++所允许的存储空间和题目要求的时间复杂度）的 maxn，当i > maxn时就停下来。

例一：HDU1166

题目中文的，一道树状数组的裸题。

题意

输入的第一行告诉你一共有n个营地。
第二行再把每个营地的初始人数告诉你。（我们当作a数组初始全0，现在执行update函数以实现a[x]+=d即可）
然后，就开始执行下面四种命令：

  1. Add i j，i 和 j 为正整数，表示第 i 个营地增加 j 个人。a[i] += j
  2. Sub i j，i 和 j 为正整数，表示第 i 个营地减少 j 个人。a[i] -= j
  3. Query i j，i 和 j 为正整数，i <= j ，表示询问第i到第j个营地的总人数。
总人数 = \sum_{x=i}^{j}{a[i]}
  1. End 表示这组命令结束。

题意捋清楚之后，有没有发现这道题很符合树状数组的特性？
读入人数，Add和Sub都用update来完成，Query用 i 和 j 的前缀和相减即可。

AC代码

#include <iostream>
#include <cstring>
#define lowbit(_x) (_x&-_x)
using namespace std;

const int maxn = 50010;///需要扩大到65536吗？

int c[maxn];

void update(int x, int val)
{
    while(x<maxn)
    {
        c[x] += val;
        x += lowbit(x);
    }
}

int getSum(int x)
{
    int sum = 0;
    while(x)
    {
        sum += c[x];
        x -= lowbit(x);
    }
    return sum;
}

int main()
{
    int caseNum; cin >> caseNum;
    for(int ct = 1; ct <= caseNum; ct++)
    {
        cout<<"Case "<<ct<<":"<<endl;
        int N; cin >> N;
        memset(c,0,sizeof(c));
        for(int i = 1; i <= N; i++)
        {
            int temp; cin >> temp;
            update(i, temp);
        }
        string str;
        while(cin >> str&&str != "End")
        {
            int i, j; cin >> i >> j;
            if(str=="Query")
            {
                cout << getSum(j) - getSum(i-1) << endl;
            }
            else if(str == "Add")
            {
                update(i, j);
            }
            else if(str == "Sub")
            {
                update(i, -j);
            }
        }
    }
    return 0;
}

未完待续......

avatar
文章
阅读
粉丝