投影地理一个核心的挑战是,地球是球形的,而显示器是平面的。我们在前面介绍了地理信息格式GeoJSON和TopoJSON,无论是这两种格式的哪一种,都是用经纬度来描述几何体或折线的。那么如何将地球上的经纬度,转化为显示器上的坐标?这就用到了D3为我们提供的Projection(投影)。
各种各样的Projection
当你查阅D3的Projection相关的API时,你会发现,D3提供了不下20种Projection。这是由于地球是一个赤道略宽两极略扁的不规则的梨形球体,故其表面是一个不可展平的曲面,所以运用任何数学方法进行这种转换都会产生误差和变形,为按照不同的需求缩小误差,就产生了各种各样的投影方法。要想深入了解D3的Projection,需要一点测绘学的知识 - 地图投射分类。D3的Projection基本上是按照地图投射分类设计的。
Azimuthal Projections(方位投影)
想象将一个平面与地球仪相切或相割,以这个平面做投影面,将地球仪上的经纬线投影到平面上,形成投影网,这就是方位投影。
方位投影将地球投射在屏幕上一定是一个圆形,因此当你想在屏幕上以圆形展现地球的时候,可以选择方位投影。
方位投影大致又分以下几种:
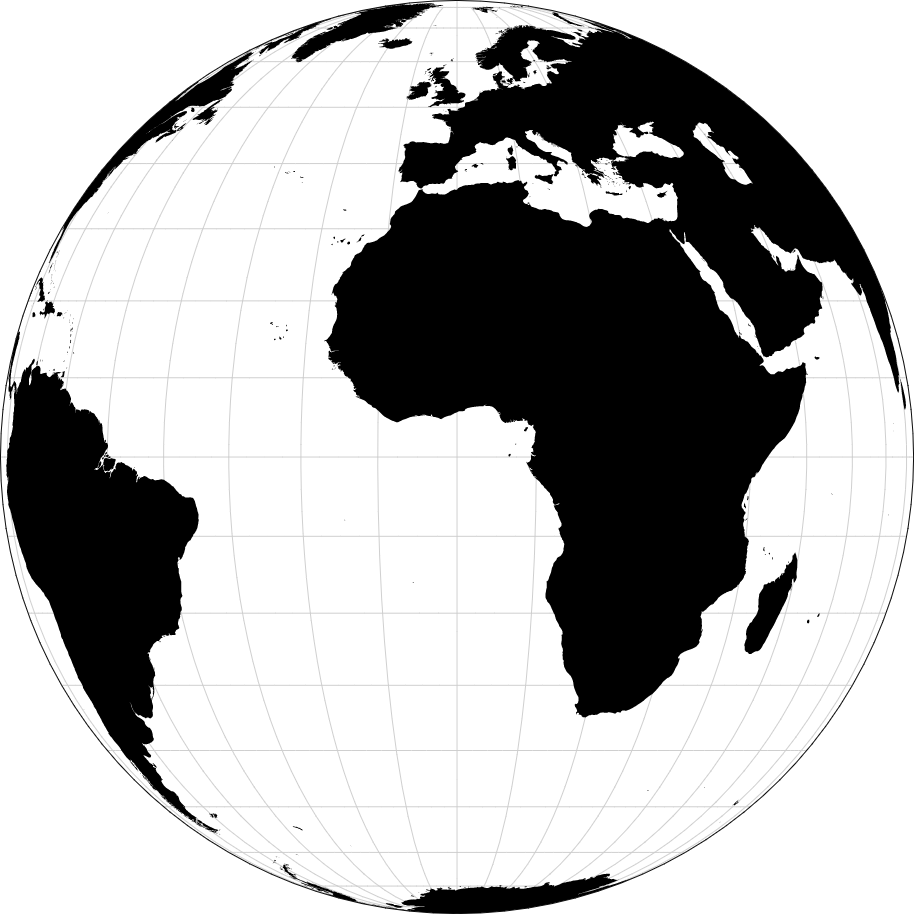
d3.geoOrthographic()
这个API返回的投影,描绘了从外层空间看,地球的形态是一个半球,在那里地平线是一个大圆。
d3.geoAzimuthalEqualArea()
这个API返回等积方位投影。 等积方位投影是使图上各点的图上面积和相应的实际地面面积比值相等的方位投影。
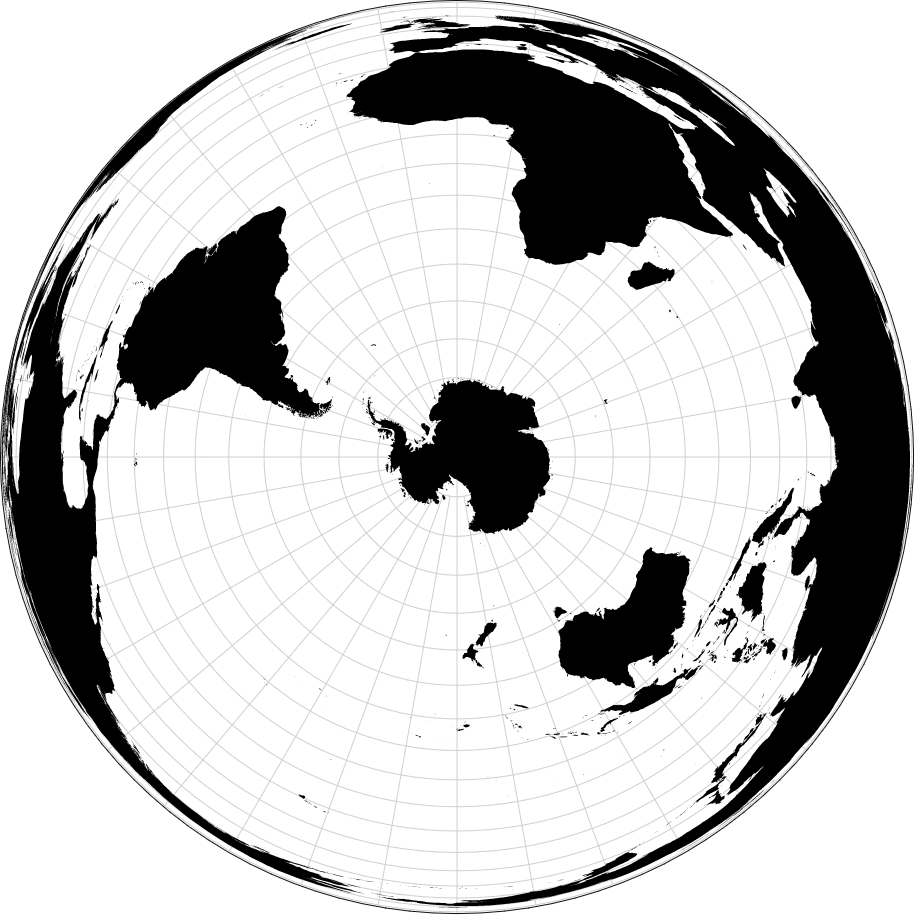
通过观察上图可以发现,与正投相比,虽然也是一个圆形,但显示的确不是一个半球的内容,而是整个地球的内容,以面积比值相等的方式展现,所投射的几何体于实际形状相比,有较大的形变。
d3.geoAzimuthalEquidistant()
这个API返回等距方位投影。
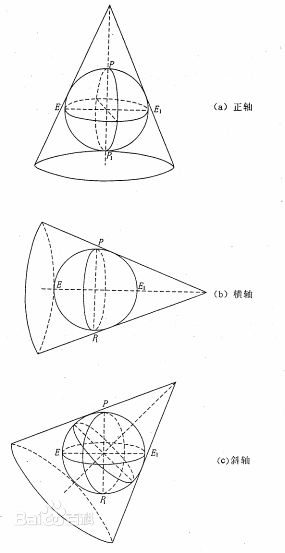
Conic Projections(圆锥投影)
设想将一个圆锥套在地球椭球体上而把地球椭球体上的经纬线网投影到圆锥面上,然后沿着某一条母线(经线)将圆锥面切开而展开成平面,就得到圆锥投影。
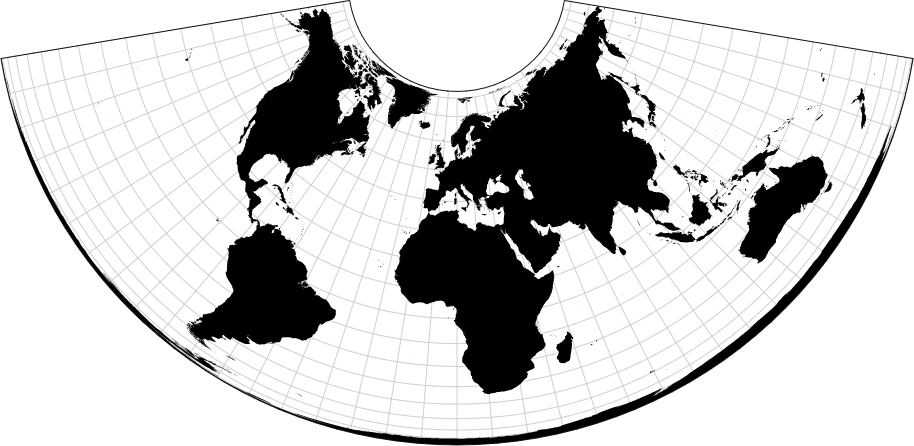
d3.geoConicEqualArea()
返回等积圆锥投影。
d3.geoConicEquidistant()
返回等距圆锥投影。
Cylindrical Projections(圆柱投影)
圆柱投影是将一个圆柱面包围椭球体,并使之相切或相割,再根据某种条件将椭球面上的经纬网点投影到圆柱面上,然后,沿圆柱面的一条母线(经线)切开,将其展成平面而得到的投影。
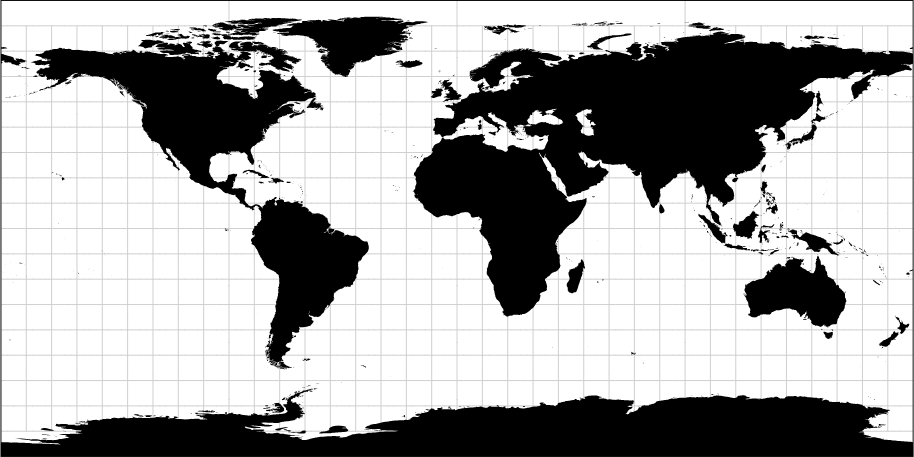
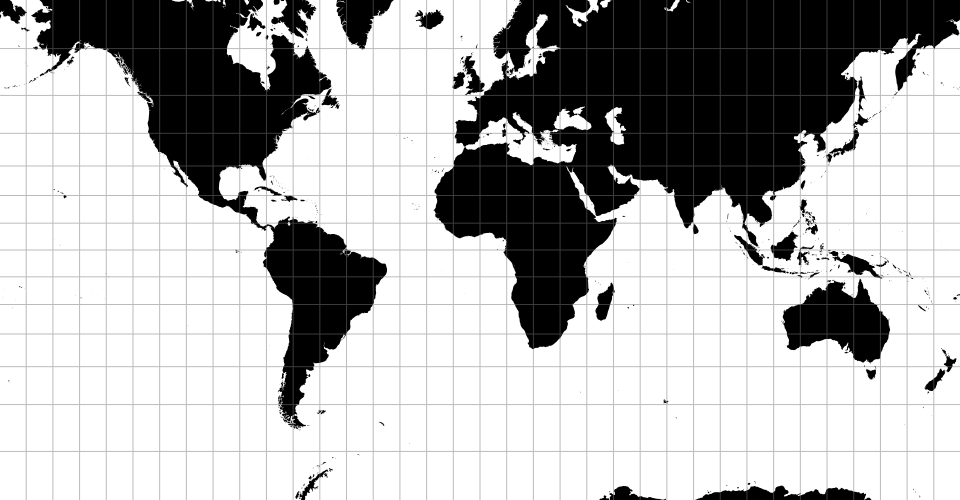
d3.geoMercator()
返回墨卡托投影。 墨卡托投影是正轴等角圆柱投影,由荷兰地图学家墨卡托(G.Mercator)于1569年创立,广泛应用于编制航海图和航空图等。
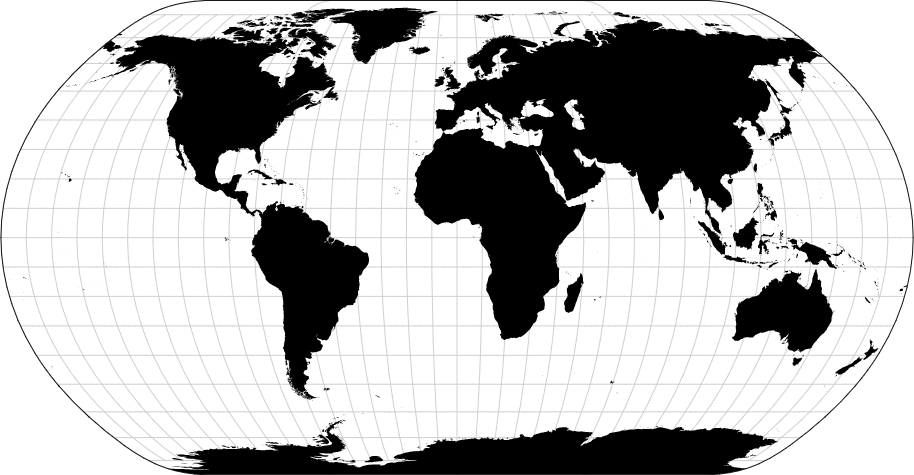
d3.geoNaturalEarth1()
自然地球投影是由汤姆·帕特森设计的一种假圆柱投影。它既不是保形的,也不是等面积的,用于绘制世界小比例尺地图。
Composite Projections (复合投影)
复合投影由多个Projection组成。
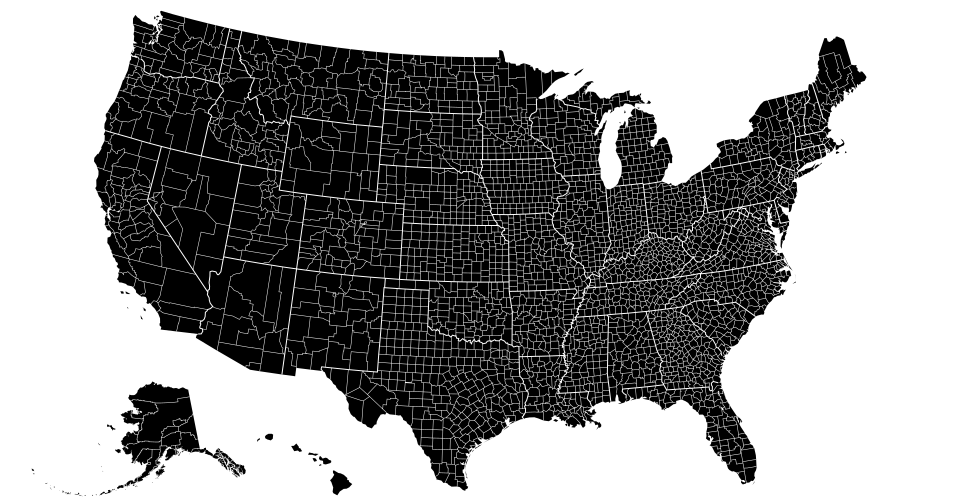
如上图的美国地图,就是由三个Projection组成的:最大的区域是48个州;左下角的阿拉斯加州;夏威夷,将三个由不同投影形成的区域组合在一起,同时阿拉斯加州还使用了较小的比例尺。复合投影适用于绘制国家版图等。
项目在GitHub上的repo:github.com/dongqiaogon…
【完】