高级数据结构系列 —— poj 2352 题解（JS版本）

好久没有刷题了，这两天在复习线段树，顺便就记录一下本题的解题过程。
点击这里看题

题目大意： 给你n个点代表n个星星，以该点为起点向x，y轴作垂线，会得到一个矩形，这个矩形里面所包含的星星数（不包括它本身）称为该星星的等级 ，要求输出在0~n-1等级各有多少个星星。注意给出的点的顺序很有讲究，是
所以其实我们只需关注每一个点在它之前出现的那些点是否在这个点与原点所围成的矩形中就行，在这个矩形中有几个点那么该点的level就是几。
比如说，我输入[[1,1], [5,1], [7,1], [3,3], [5,5]]，先看第一个点，[1,1]之前还没有点出现，所以很明显[1,1]的level就是0，level[0] ++，对于第二个点，[5,1]与原点所围成的矩形中出现了[1,1]，所以[5,1]的level就是1，level[1] ++，第三个点[7,1]与原点围成的矩形中有[1,1]和[5,1]，那么[7,1]的level就是2，level[2] ++；对于[3,3]，它与原点所围成的矩形中是[1,1], 所以[3,3]的level是1，level[1] ++；最后是[5,5]，它与原点围成的矩形中有[1,1]，[5,1]和[3,3]，所以[5,5]的level就是3，level[3] ++; 所以最后得出来的level数组为[1,2,1,1,0].
到这里，相信你已经看懂了题目，那么该怎么解呢？

暴力法

暴力大家应该都想得出来，两重for循环，既然y坐标是按照升序的，那么我只要考虑在当前点之前的点的x坐标是否不大于当前点的x坐标即可，第一重for里面代表是当前点，第二重for是当前点之前的点。

思考一下

如果用暴力的话，对于数据量比较小的时候还能hold得住，但是数据量一大呢，两重for的时间复杂度可是O(n^2),如果我输入的是一万个数呢，那么就要跑10000 * 10000次啊，要是再多点呢？显然这是不行的。那么我们再思考一下，对于某个点(tx, ty)，它的y坐标我们不用考虑了，对于x坐标，我们只要找出在它之前出现的点中，哪些点的x坐标不就行了吗，统计出来假设有n个点，那么level[n]++ 即可。所以问题到这边就转换成了的问题了。熟悉线段树的同学应该知道线段树就是用来高效解决这类求区间和的问题的，还不了解线段树的点击这里

线段树解法

我们用线段树去维护star的x区间，每次读入一个点，就去更新线段树(这里我把建树和更新放在一起操作了)，更新完之后就去读取区间和，代码如下：

       var maxn = 0;  //x坐标的边界
       var level = [];
       var tree = [];  //维护x坐标区间
       function getStarLevel(stars) {
           maxn = 0;
           level = [];
           for(let i = 0; i < stars.length; i ++)
               level[i] = 0;
           tree = [];
           for(let i = 0; i < stars.length; i ++) {
               if(stars[i][0] > maxn)
                   maxn = stars[i][0];
           }
           for(let i = 0; i < 4 * maxn; i ++)  //线段树的缺点，空间消耗大
               tree[i] = 0; //初始化线段树
           for(let i = 0; i < stars.length; i ++) {
               build_tree(1, 0, maxn, stars[i][0]);  //在线建树
               level[find(1, 0, maxn, 0, stars[i][0]) - 1] ++; //这边 -1 是不能把自身给算上去
           }

           return level;
       }

       /*
       * 递归建树
       * */
       function build_tree(id, left, right, x) {
           if(left === right) {
               tree[id] ++;
               return;
           }
           let mid = (left + right) >> 1;
           if(mid >= x)
               build_tree(id << 1, left, mid, x);
           else
               build_tree(id << 1 | 1, mid + 1, right, x);
           tree[id] = tree[id << 1] + tree[id << 1 | 1];
       }

       function find(id, minX, maxX, left, right) {
           if(minX === left && maxX === right)
               return tree[id];
           let mid = (minX + maxX) >> 1;
           if(right <= mid)
               return find(id << 1, minX, mid, left, right);
           else if(left > mid)
               return find(id << 1 | 1, mid + 1, maxX, left, right);
           else
               return find(id << 1, minX, mid, left, mid) + find(id << 1 | 1, mid + 1, maxX, mid + 1, right);
       }

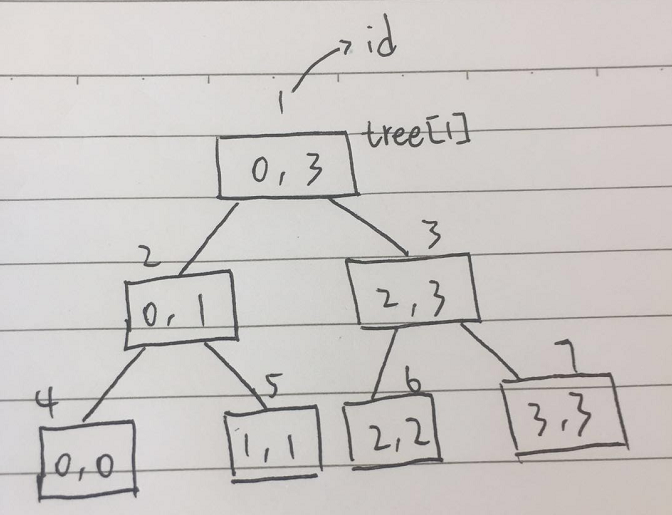
这里用个简单的例子来讲解一下这段代码，[[1,1], [2,2], [3,1]]，首先我是遍历一遍点去拿到x的边界值即maxn=3，也就是说，我们需要维护的就是一个[0,3]的区间，该树如下图所示

注意每个节点上面的数字是它的id，每个节点框里面的数字代表的是区间，也就是说tree[1]代表的就是区间[0,3]的和，每次的更新操作(这里我直接把更新和建树合并了，就是build_tree函数)其实本质上改变的是叶子节点的值，当读入第一个点[1,1]时，它的x坐标是1，我们从树根往下递归，发现tree[5]代表的就是x=1，所以tree[5] ++，此时tree[5]就是1，之后又会从叶子往上更新，找到tree[5]的父节点，即tree[2]，也更新为了1，再往上，tree[1]也更新为1，更新完了之后查找在第一个点之前有没有点的x坐标是小于第一个点的x坐标即1的，即查询[0,1]区间的和，代码还是从树根开始找，发现树根代表的是[0,3]的区间和，二分后递归查找左子树，发现左子树代表的是[0,1],正好就是该区间，所以之间返回tree[2]节点的值即可，之后的更新查找操作就和第一次的一样了，这里就不赘述了。

小结

线段树虽然能节省时间上的开支，但是也是建立在了开出很多数组的前提下，是一种以空间换时间的解决方案，其实涉及区间和，单点更新的题也可以用树状数组来做，时间复杂度和线段树一样，但是空间上能省出很多来，有兴趣的可以自己去了解一下，本题也可以用树状数组解决