【数据结构】AVL（平衡二叉树）的基础实现

Autu
223 阅读4分钟

定义

对于任意一个节点，左子树和右子树的高度相差不能超过1.（这里的定义不是标准的平衡二叉树）

高度为h的 AVL 树，节点数N最多为

img
最少节点数
img
(
img
是 Fibonacci polynomial 的第h+2个数）。

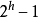
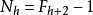
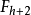
换句话说，当节点数为 N 时，高度 h 最多为

img
标注节点高度

每个节点的高度为其最高子树的高度+1

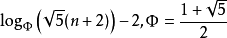
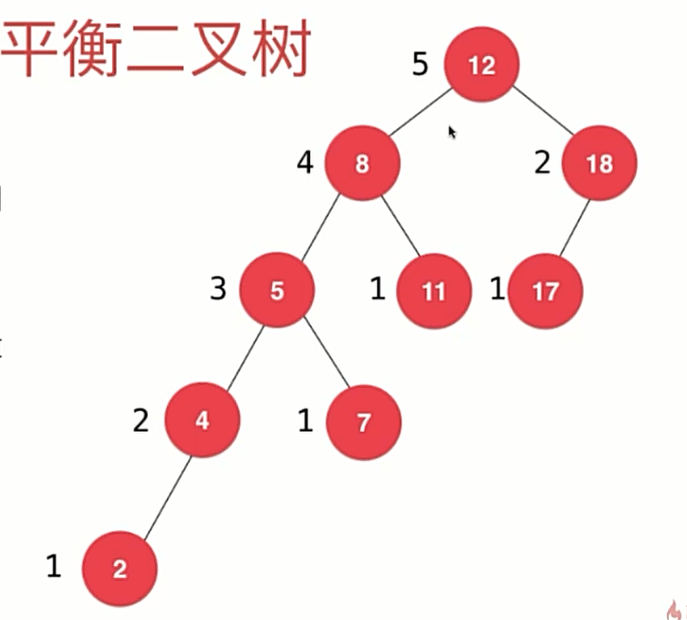
平衡因子

每个节点的平衡因子为其左右子树的高度差。

一个节点的平衡因子超过1或小于-1时就破坏了我们的平衡二叉树的定义。

基本数据结构

public class AVLTree<K extends Comparable<K>, V> {

    private class Node{
        public K key;
        public V value;
        public Node left, right;
        public int height;

        public Node(K key, V value){
            this.key = key;
            this.value = value;
            left = null;
            right = null;
            height = 1;
        }
    }

    private Node root;
    private int size;

    public AVLTree(){
        root = null;
        size = 0;
    }

    public int size(){
        return size;
    }

    public boolean isEmpty(){
        return size == 0;
    }

    private int getHeight(Node node){
        if (node == null){
            return 0;
        }
        return node.height;
    }

    /**
     * 计算平衡因子
     */
    private int getBalanceFactor(Node node){
        if (node == null){
            return 0;
        }
        return getHeight(node.left) - getHeight(node.right);
    }
    
    public void add(K key, V value){
        root = add(root, key, value);
    }

    private Node add(Node node, K key, V value){

        if (node == null){
            size++;
            return new Node(key, value);
        }

        /**
         * 更新height
         */
        node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
        /**
         * 计算平衡因子
         */
        int balanceFactor = getBalanceFactor(node);

        return node;
    }
}

旋转操作的基本原理

维护平衡的时机

二分搜索树在添加新节点时可能会失去平衡，而失去平衡的节点只可能在新节点的祖先节点上。所以需要从新节点向上维护平衡性。

右旋转

插入元素在不平衡节点的左侧的左侧时使用

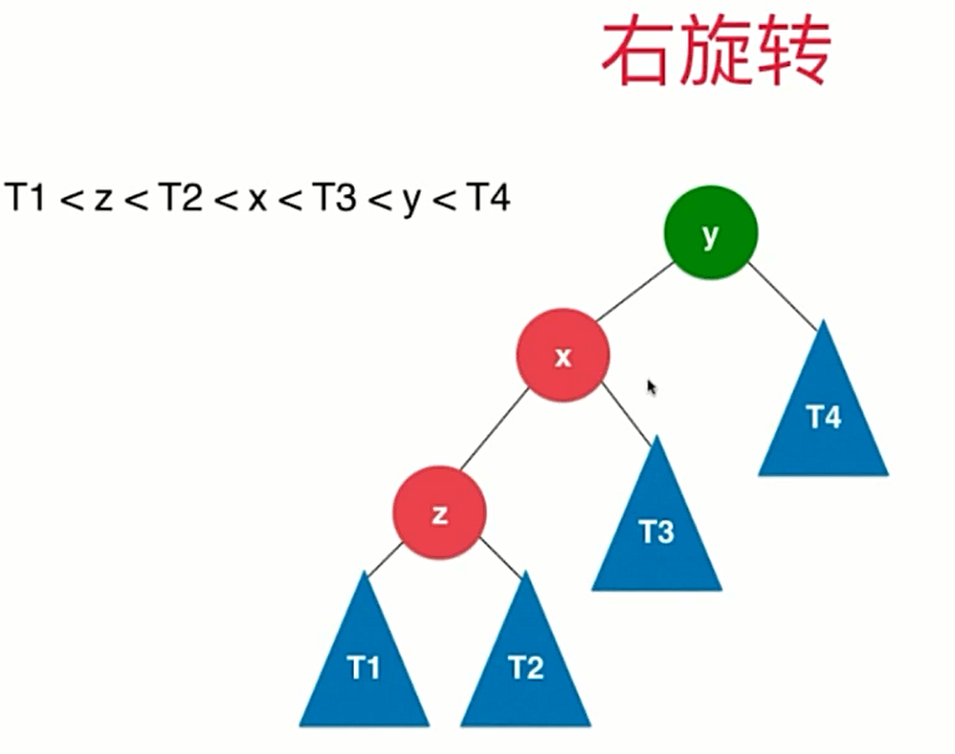
如图的二分搜索树其值大小如左上角所示

对于这颗二分搜索树的右旋转操作为

x.right = y;
y.left = T3;

旋转以后的树如下图

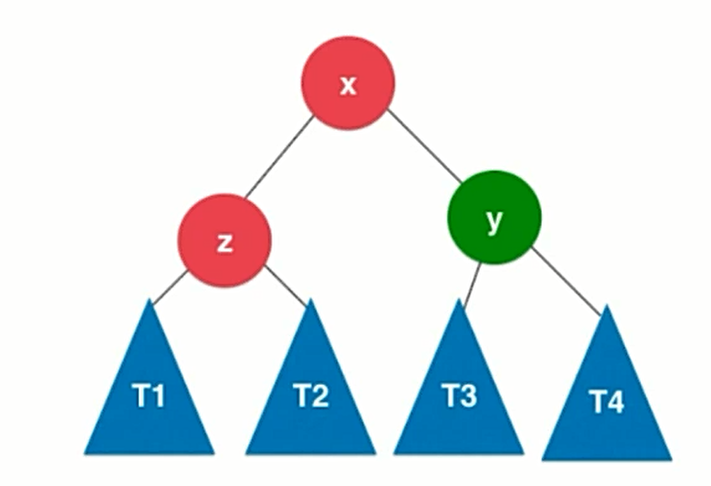
由前面的大小关系我们可以知道对于这颗树它依然满足二分搜索树的性质，同时它也是平衡二叉树，具体原因可以从数学角度证明，这里不详细说了。

代码实现

/**
 * 对节点y进行右旋转操作，返回旋转后的根节点
 * @param y
 * @return
 */
private Node rightRotate(Node y){

    Node x = y.left;
    Node T3 = x.right;

    /**
     * 向右旋转过程
     */
    x.right = y;
    y.left = T3;

    /**
     * 更新height
     */
    y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
    x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;

    return x;
}

左旋转

插入元素在不平衡节点的右侧的右侧时

旋转以后

操作过程代码

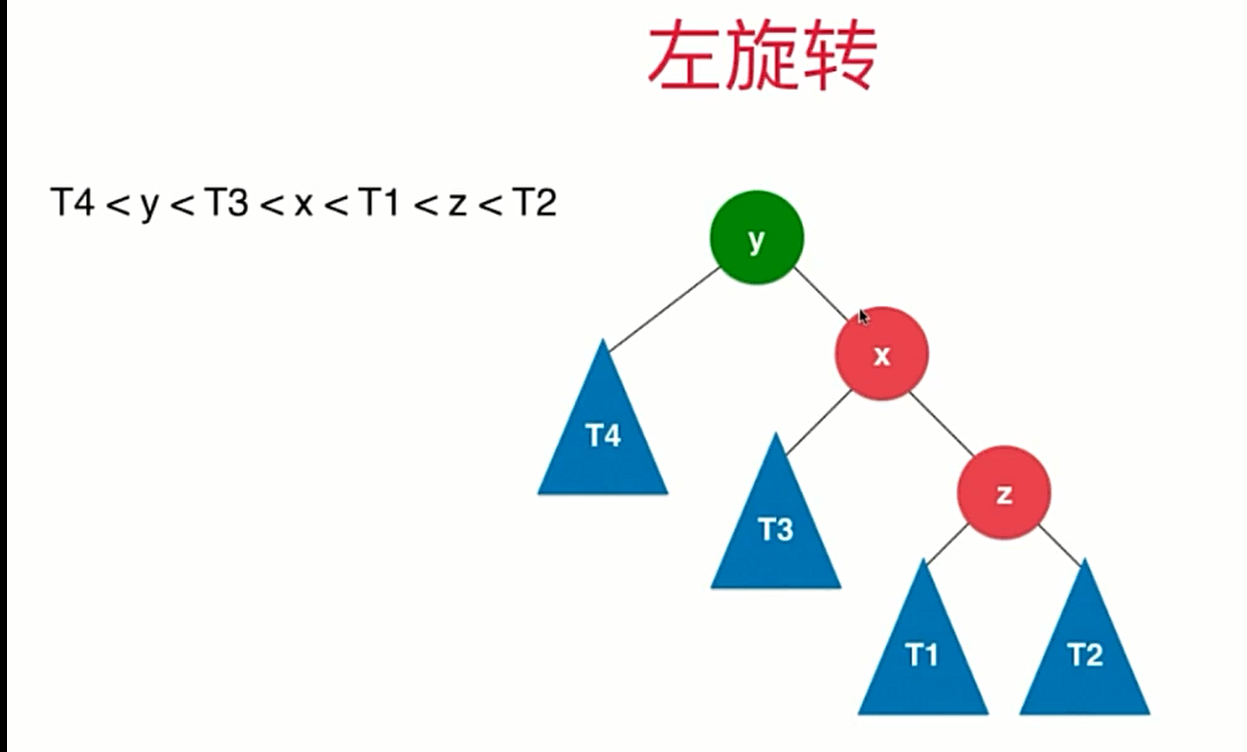
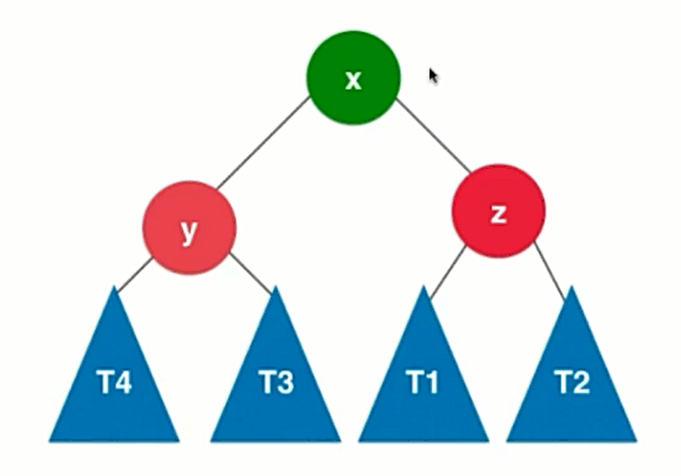
x.left = y;
y.right = T3;

方法实现

/**
 * 左旋转操作
 * @param y
 * @return
 */
private Node leftRotate(Node y){

    Node x = y.left;
    Node T2 = x.right;

    /**
     * 向左旋转过程
     */
    x.right = y;
    y.right = T2;

    /**
     * 更新height
     */
    y.height = Math.max(getHeight(y.left), getHeight(y.right)) + 1;
    x.height = Math.max(getHeight(x.left), getHeight(x.right)) + 1;

    return x;
}

其他的情况

当插入的元素在不平衡节点的左侧的右侧时

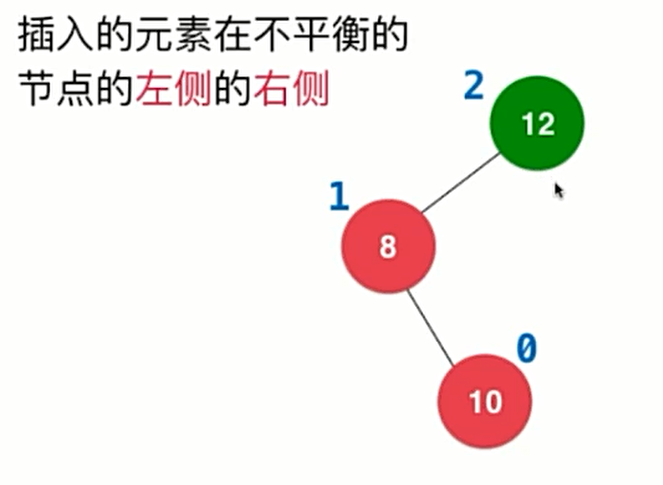
这时右旋转就不能解决这个问题了，因为10和12都比8这个节点大。

LR

这样以后就可以按照之前的方法来平衡了。

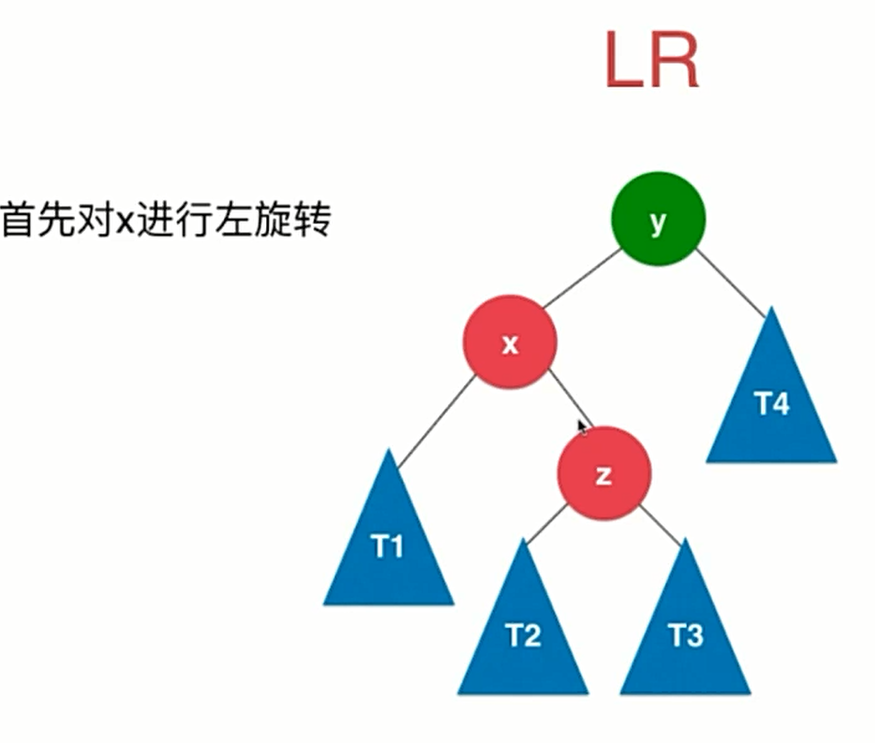
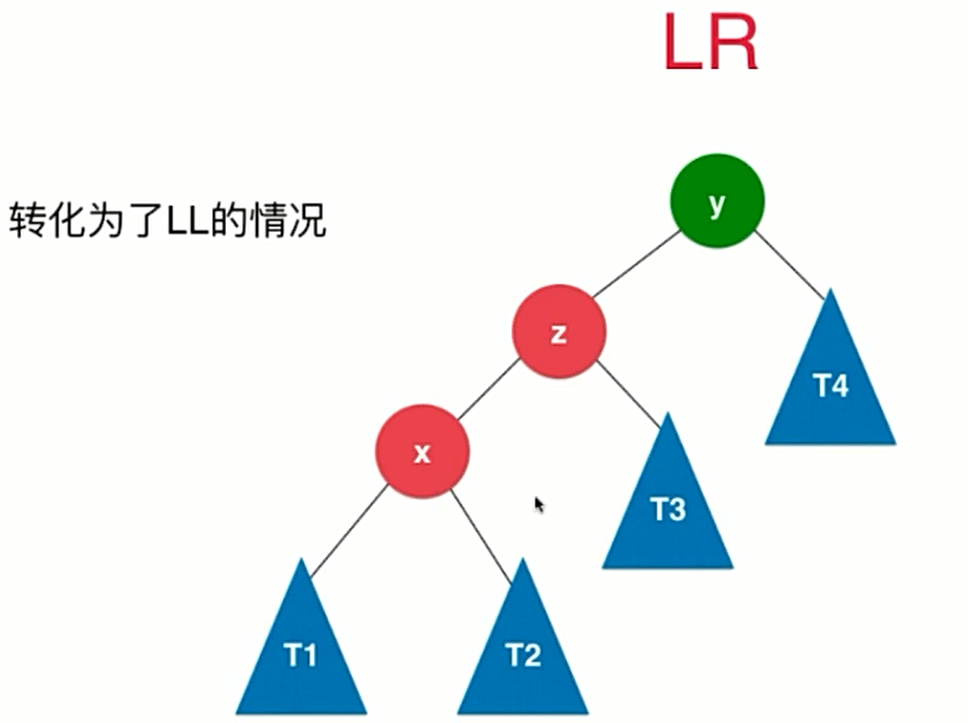
RL的情况与LR同理，把左右换一下就行了。

向AVL中添加元素的方法

public void add(K key, V value){
    root = add(root, key, value);
}

private Node add(Node node, K key, V value){

    if (node == null){
        size++;
        return new Node(key, value);
    }

    if (key.compareTo(node.key) < 0){
        node.left = add(node.left, key, value);
    }
    else if (key.compareTo(node.key) > 0){
        node.right = add(node.right, key, value);
    }
    else {
        node.value = value;
    }

    /**
     * 更新height
     */
    node.height = 1 + Math.max(getHeight(node.left), getHeight(node.right));
    /**
     * 计算平衡因子
     */
    int balanceFactor = getBalanceFactor(node);

    /**
     * 平衡维护
     */
    //LL
    if (balanceFactor > 1 && getBalanceFactor(node.left) >= 0){
        return rightRotate(node);
    }
    //RR
    if (balanceFactor < -1 && getBalanceFactor(node.right) <= 0){
        return leftRotate(node);
    }
    //LR
    if (balanceFactor > 1 && getBalanceFactor(node.left) < 0){
        node.left = leftRotate(node.left);
        return rightRotate(node);
    }
    //RL
    if (balanceFactor < -1 && getBalanceFactor(node.right) > 0){
        node.right = rightRotate(node.right);
        return leftRotate(node);
    }
    return node;
}

从AVL中删除元素

删除节点的逻辑与二分搜索树删除节点的基础上加上了height和平衡性的维护即可。

实现代码

/**
 * 从二分搜索树中删除节点
 * @param key
 */
public void remove(K key){
    root = remove(root, key);
}

private Node remove(Node node, K key){

    if (node == null){
        return null;
    }

    Node retNode;
    if (key.compareTo(node.key) < 0){
        node.left = remove(node.left, key);
        retNode = node;
    }
    else if (key.compareTo(node.key) > 0){
        node.right = remove(node.right, key);
        retNode = node;
    }
    else {
        //待删除节点左子树为空的情况
        if (node.left == null){
            Node rightNode = node.right;
            node.right = null;
            size--;
            retNode =  rightNode;
        }

        //待删除节点右子树为空的情况
        else if (node.right == null){
            Node leftNode = node.left;
            node.left = null;
            size--;
            retNode = leftNode;
        }

        //待删除节点左右子树均不为空的情况
        //找到比待删除节点大的最小节点，即待删除节点右子树的最小节点，用这个节点顶替待删除节点的位置
        else {
            Node successor = minimum(node.right);
            successor.right = remove(node.right, successor.key);
            successor.left = node.left;

            node.left = node.right = null;
            retNode = successor;
        }
    }

    if (retNode == null){
        return null;
    }

    /**
     * 更新height
     */
    retNode.height = 1 + Math.max(getHeight(retNode.left), getHeight(retNode.right));
    /**
     * 计算平衡因子
     */
    int balanceFactor = getBalanceFactor(retNode);

    /**
     * 平衡维护
     */
    //LL
    if (balanceFactor > 1 && getBalanceFactor(retNode.left) >= 0){
        return rightRotate(retNode);
    }
    //RR
    if (balanceFactor < -1 && getBalanceFactor(retNode.right) <= 0){
        return leftRotate(retNode);
    }
    //LR
    if (balanceFactor > 1 && getBalanceFactor(retNode.left) < 0){
        node.left = leftRotate(retNode.left);
        return rightRotate(retNode);
    }
    //RL
    if (balanceFactor < -1 && getBalanceFactor(retNode.right) > 0){
        node.right = rightRotate(retNode.right);
        return leftRotate(retNode);
    }
    return retNode;
}

因为树的高度为 log(n), 旋转的时间复杂度为 O(1), 故删除的时间复杂度仍为O(log(n))。

Written by Autu

2019.7.4

avatar
文章
阅读
粉丝