给定一个32位的整数n,这个数可以为0,可以为正,可以为负,求给定整数二进制数中1的个数
例如:
十进制 566
二进制 1000110110
返回 5
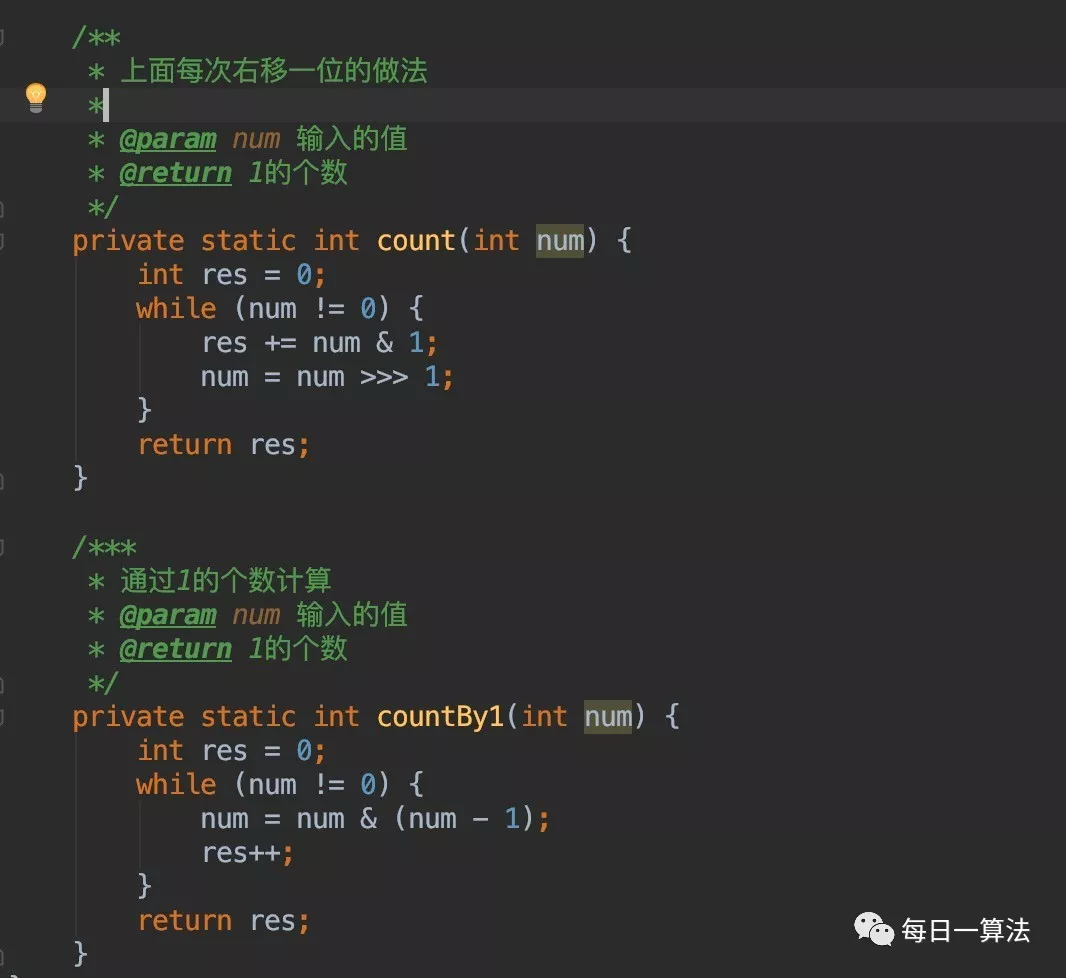
1:最简单的解法,把整数n每次都无符号向右移动一位,检查最右边的bit位是否为1来统计,当n=0的时候,也就是循环完成的时候。
2:上面的这个方法在最复杂的情况下需要经过32次循环,那么是不是可以考虑循环的次数和1有关的解法呢?
例如:
n=566 二进制为1000110110
n=565 二进制为1000110101
==========================
n&(n-1) 二进制为1000110100
仔细观察上面3行,可以发现什么规律呢?思考5分钟......
如果不明白的话,我们可以继续往下计算
n 1000110100
n-1 1000110011
==================
n&(n-1) 1000110000
n 1000110000
n-1 1000101111
==================
n&(n-1) 1000100000
n 1000100000
n-1 1000011111
==================
n&(n-1) 1000000000
n 1000000000
n-1 0111111111
==================
n&(n-1) 0000000000
结论:每次最后面的一位的1,通过一次“与”运算,可以被去掉。当最后得到的数字为0的时候,运算结束。
感谢大家阅读到此,如果你觉得这篇文章有用,记得分享关注下面的公众号,大家一起进步哦~~~

扫一扫 关注我的公众号
如果你想要跟大家分享你的文章,欢迎留言投稿~
如果你喜欢,请留下你的赞哦