优先队列

定义：出队顺序和入队顺序无关，和优先级相关。

应用：操作系统中动态选择优先级最高的任务执行。

底层实现	入队	出队（拿出最大元素）
普通线性结构	O(1)	O(n)
顺序线性结构	O(n)	O(1)
堆	O(logn)	O(logn)

二叉堆

二叉堆是一颗完全二叉树。

堆中某个节点的值总是不大于其父节点的值。这样得到的堆叫最大堆（相应的可以定义最小堆）

这里我们使用数组来表示一个二叉堆，如图所示。

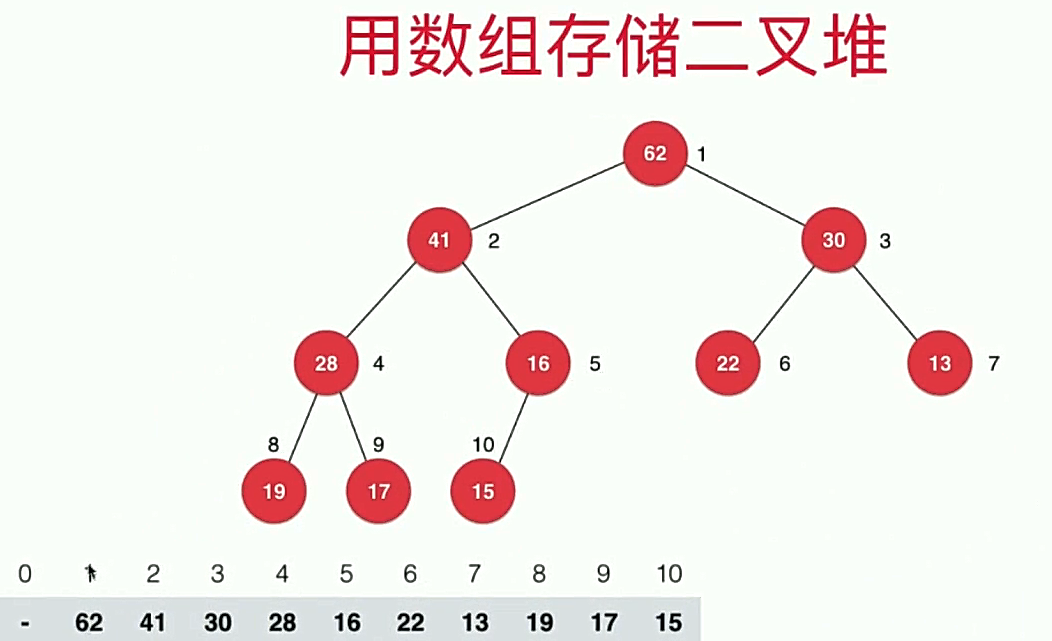
由图我们可以发现：对于任意一个节点，它的左右孩子的节点索引是它本身的2倍和2倍加1.

用代码来表示就是

parent(i) = i/2;
left child(i) = 2*i;
right child(i) = 2*i + 1;

二叉堆的基本操作

public class MaxHeap<E extends Comparable<E>> {

    private Array<E> data;

    public MaxHeap(int capacity){
        data = new Array<>(capacity);
    }

    public MaxHeap(){
        data = new Array<>();
    }

    public int size() {
        return data.getSize();
    }

    public boolean isEmpty(){
        return data.isEmpty();
    }

    /**
     * 返回完全二叉树的数组表示中，一个索引表示的元素的父亲节点的索引
     * @param index
     * @return
     */
    private int parent(int index){
        if (index == 0){
            throw new IllegalArgumentException("index-0 doesn't have parent");
        }
        return (index - 1) / 2;
    }

    /**
     * 返回完全二叉树的数组表示中，一个索引表示的元素的左孩子节点的索引
     * @param index
     * @return
     */
    private int  leftChild(int index){
        return index * 2 + 1;
    }

    /**
     * 返回完全二叉树的数组表示中，一个索引表示的元素的右孩子节点的索引
     * @param index
     * @return
     */
    private int rightChild(int index){
        return index * 2 + 2;
    }
}

向堆中添加元素

首先我们要明白堆中添加元素的机制：待添加的节点不断地与它的父节点比较，若大于父节点则交换两个节点的位置，直到添加节点的值小于其父节点。我们可以把这个过程理解为上浮。

在实现这个操作之前我们需要写一个辅助的函数来使后面的实现变得简单。

首先因为我们使用的堆的底层实现是基于数组，所以我们要在Array类中添加一个swap方法用于交换两个数组索引的值。

public void swap(int i, int j){

    if (i < 0 || i >= size || j < 0 || j >= size){
        throw new IllegalArgumentException("Index is illegal.");
    }

    E t = data[i];
    data[i] = data[j];
    data[j] = t;
}

最后就可以实现添加元素的add方法了

/**
 * 向堆中添加元素
 * @param e
 */
public void add(E e){
    data.addLast(e);
    siftUp(data.getSize() - 1);
}

从堆中取出元素

对于最大堆来说，我们取出元素时只取出最大的那个元素，即堆顶的元素。

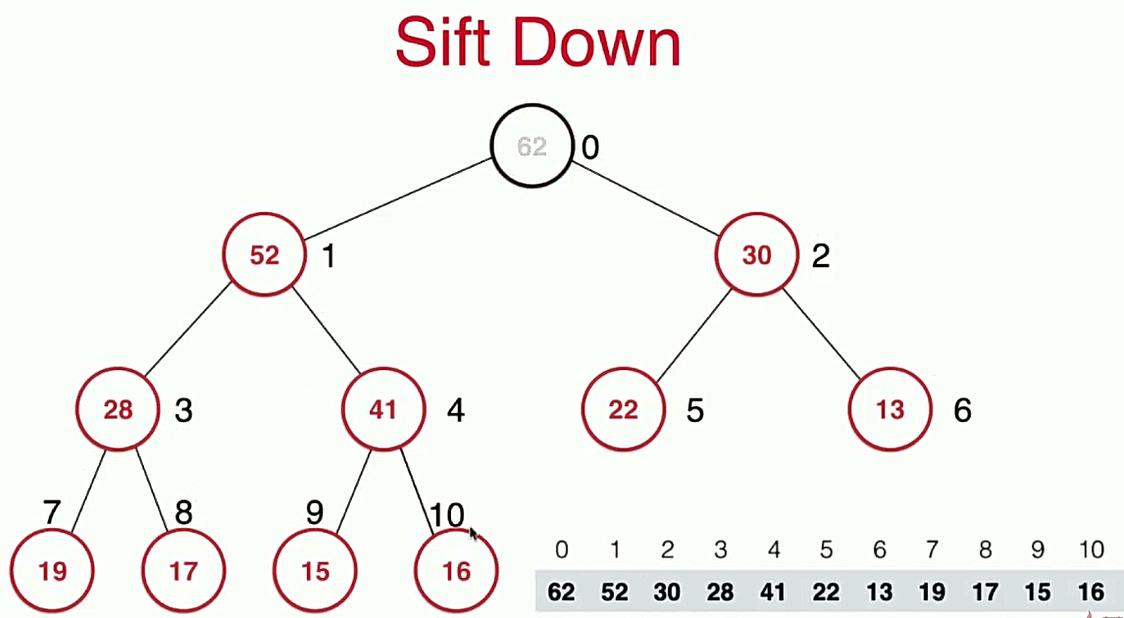
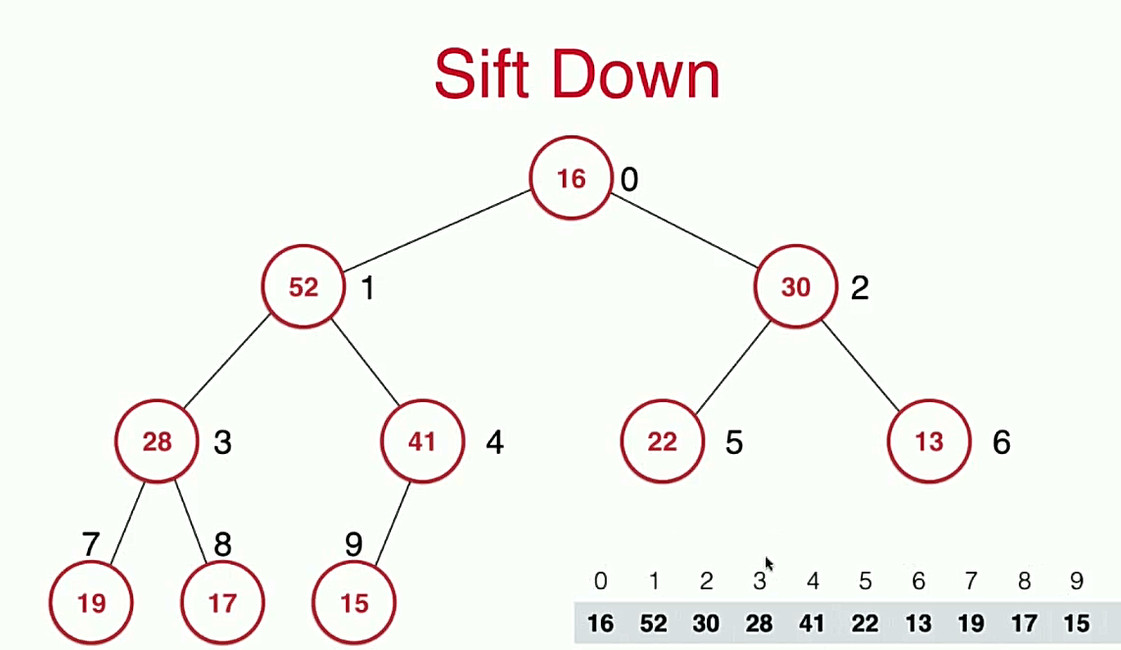
如图当我们需要删除62这个节点时，我们只需要把数组的0号位置上的值删除即可，但是这样做以后我们需要合并两个子树会比较麻烦。所以这里用这个堆的最后一个元素来覆盖这个堆的根节点的元素，然后我们把最后的节点删去，这样就成功删掉了一个节点。接下来就是要让这个新的堆满足最大堆的性质，也就是让当前的堆顶元素下沉（Sift Down）。

下沉操作实现的过程：堆顶元素与它的左右孩子元素的值比较，与左右孩子中最大的那个元素交换位置，然后继续比较，直到该节点的值大于其左右孩子的节点值。

代码实现：

/**
 * 看堆中最大元素
 * @return
 */
public E findMax() {

    if (data.getSize() == 0){
        throw new IllegalArgumentException("heap is empty!");
    }
    return data.get(0);
}

/**
 * 取出堆中最大元素
 * @return
 */
public E extraMax(){

    E ret = findMax();

    data.swap(0, data.getSize() - 1);
    data.removeLast();
    siftDown(0);

    return ret;
}

private void siftDown(int k){

    while (leftChild(k) < data.getSize()){

        int j = leftChild(k);
        if (j + 1 < data.getSize() && data.get(j + 1).compareTo(data.get(j)) > 0){
            j = rightChild(k);
        }
        //此时data[j] 是左右孩子中的最大值

        if (data.get(k).compareTo(data.get(j)) >= 0){
            break;
        }
        data.swap(k, j);
        k = j;
    }
}

add和extraMax的时间复杂度都是O（logn）

Heapify 和 replace

replace

replace: 取出最大元素后，放入一个新的元素。

实现：可以先extraMax，再add，两次O（logn）的操作。

这样的方法可以实现，但是还可以优化成一次O（logn）的操作。

优化实现：可以直接将堆顶元素替换以后SiftDown。

/**
 * 取出堆中最大元素， 并且替换成元素e
 * @param e
 * @return
 */
public E replace(E e){

    E ret = findMax();
    data.set(0, e);
    siftDown(0);
    return ret;
}

Heapify

定义：将任意数组整理成堆的形状。

实现思路：

首先我们将任意的数组按照索引看成一个堆，如图所示。

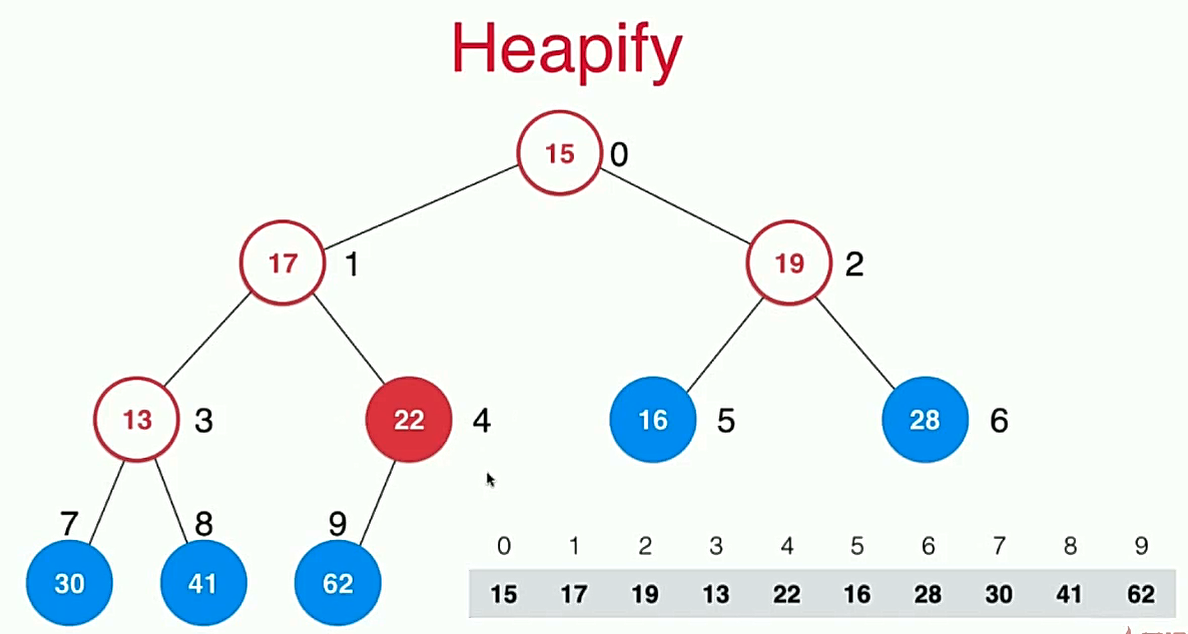
然后我们从最后一个非叶子节点开始对其做siftDown操作。这里有一个经典的问题就是如何获取一个完全二叉树的最后一个非叶子节点的索引，其实很简单就是获取最后一个节点的父节点即可。

heapify的算法复杂度

将n个元素逐个插入到空堆中的复杂度是O(nlogn)

heapify的过程复杂度为O(n)

代码实现

首先在Array类中添加新的构造函数

public Array(E[] arr){
    data = (E[])new Object[arr.length];
    for (int i = 0; i < arr.length; i++){
        data[i] = arr[i];
    }
    size = arr.length;
}

然后在MaxHeap中添加构造函数

public MaxHeap(E[] arr){
    data = new Array<>();
    for(int i = parent(arr.length - 1); i >= 0; i--){
        siftDown(i);
    }
}

这样就完成了heapify的实现了。

基于堆的优先队列

/**
 * className PriorityQueue
 * description TODO
 *
 * @author ln
 * @version 1.0
 * @date 2019/5/24 14:47
 */
public class PriorityQueue<E extends Comparable<E>> implements Queue<E> {

    private MaxHeap<E> maxHeap;

    public PriorityQueue(){
        maxHeap = new MaxHeap<>();
    }

    @Override
    public int getSize() {
        return maxHeap.size();
    }

    @Override
    public boolean isEmpty() {
        return maxHeap.isEmpty();
    }

    @Override
    public void enqueue(E e) {
        maxHeap.add(e);
    }

    @Override
    public E dequeue() {
        return maxHeap.extraMax();
    }

    @Override
    public E getFront() {
        return maxHeap.findMax();
    }
}

可以看到用最大堆来实现优先队列是非常方便的。

Writtern by Autu.

2019.6.30

【数据结构】基于二叉堆的优先队列基础实现