二叉树遍历

二叉树结点数据结构

class BiTree<T> {
    var value: T
    var lchild: BiTree?
    var rchild: BiTree?
    init(value: T) {
        self.value = value
        self.lchild = nil
        self.rchild = nil
    }
}

前序遍历(NLR) ：若二叉树为空，则空操作返回，否则先访问根结点，然后前序遍历左子树，再前序遍历右子树。

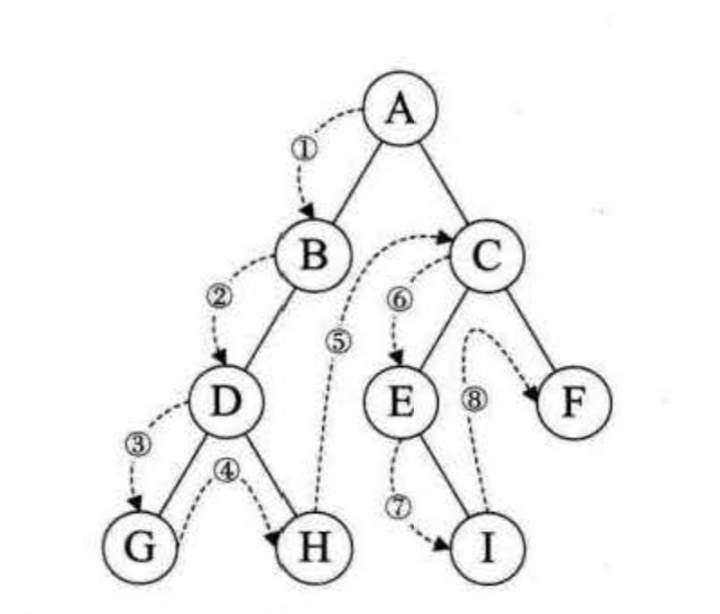
func preOrderTraverse<T>(tree: BiTree<T>?) {
    guard let tree = tree else { return }
    print(tree.value)   //显示结点数据，可更改为其他操作
    preOrderTraverse(tree: tree.lchild)     //遍历左子树
    preOrderTraverse(tree: tree.rchild)     //遍历右子树
}

中序遍历(LNR) ：若树为空，则空操作返回，否则从根结点开始(注意并不是先访问根结点) ，中序遍历根结点的左子树，然后是访问根结点，最后中序遍历右子树。

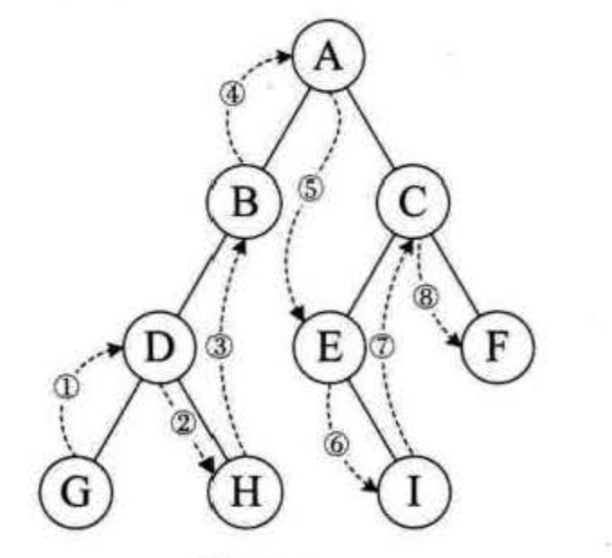
func inOrderTraverse<T>(tree: BiTree<T>?) {
    guard let tree = tree else { return }
    inOrderTraverse(tree: tree.lchild)     //遍历左子树，找到最左边结点
    print(tree.value)   //显示结点数据，可更改为其他操作
    inOrderTraverse(tree: tree.rchild)     //遍历右子树
}

后序遍历(LRN) ：若树为空，则空操作返回，否则从左到右先叶子后结点的方式遍历访问左、右子树，最后是访问根结点。

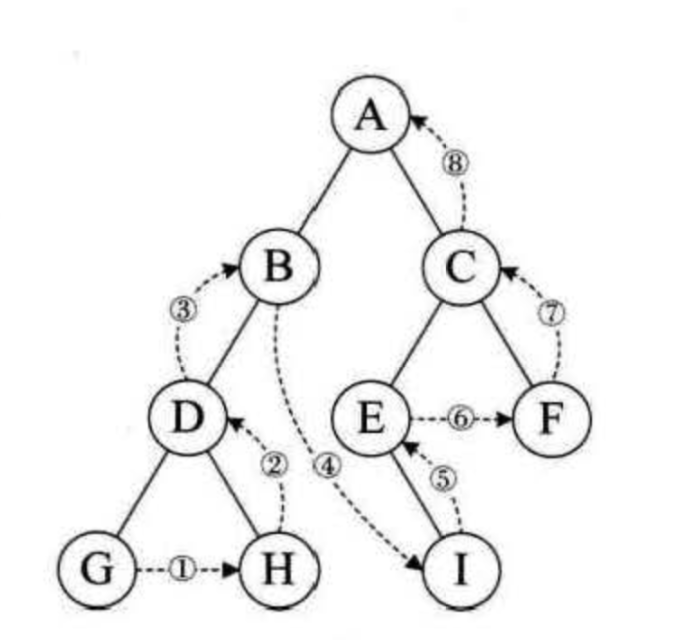
func postOrderTraverse<T>(tree: BiTree<T>?) {
    guard let tree = tree else { return }
    postOrderTraverse(tree: tree.lchild)    //遍历左子树
    postOrderTraverse(tree: tree.rchild)    //遍历右子树
    print(tree.value)   //显示结点数据，可更改为其他操作
}

层序遍历 ：若树为空，则空操作返回，否则从树的第一层，也就是根结点开始访问，从上而下逐层遍历，在同一层中，按从左到右的顺序对结点逐个访问。

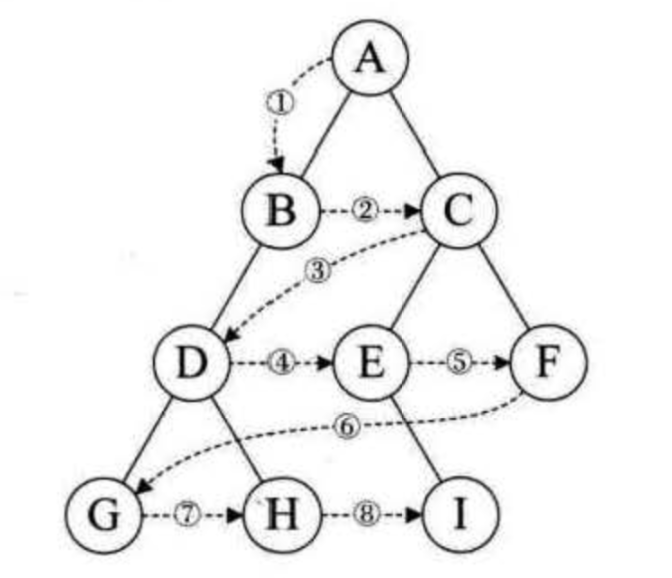
//层序遍历加入了一个数组(队列)进行辅助实现
func levelOrderTraverse<T>(tree: BiTree<T>?) {
    guard let tree = tree else { return }
    var list = [BiTree<T>]()
    list.append(tree)
    while list.isEmpty {
        let node = list.first
        print(node!.value)      //显示结点数据，可更改为其他操作
        if let left = node!.lchild {
            list.append(left)
        }
        if let right = node!.rchild {
            list.append(right)
        }
        list.removeFirst()
    }
}