题目
给定一个 n × n 的二维矩阵表示一个图像。
将图像顺时针旋转 90 度。
说明:
你必须在原地旋转图像,这意味着你需要直接修改输入的二维矩阵。请不要使用另一个矩阵来旋转图像。
示例 1:
给定 matrix =
[
[1,2,3],
[4,5,6],
[7,8,9]
],
原地旋转输入矩阵,使其变为:
[
[7,4,1],
[8,5,2],
[9,6,3]
]
示例 2:
给定 matrix =
[
[ 5, 1, 9,11],
[ 2, 4, 8,10],
[13, 3, 6, 7],
[15,14,12,16]
],
原地旋转输入矩阵,使其变为:
[
[15,13, 2, 5],
[14, 3, 4, 1],
[12, 6, 8, 9],
[16, 7,10,11]
]
来源:力扣(LeetCode)
链接:https://leetcode-cn.com/problems/rotate-image
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解
先从起点开始入手, 1 -> 3 -> 9 -> 7 -> 1。很显然,每旋转一个点,就会有其他联动的三个点,同时移动位置,所以说,只需要旋转四分之一的图像,完成之后,也就完成了整个矩阵的旋转。下面就是确定,从点(x,y) 旋转之后到了什么位置,可以参见下面的草图
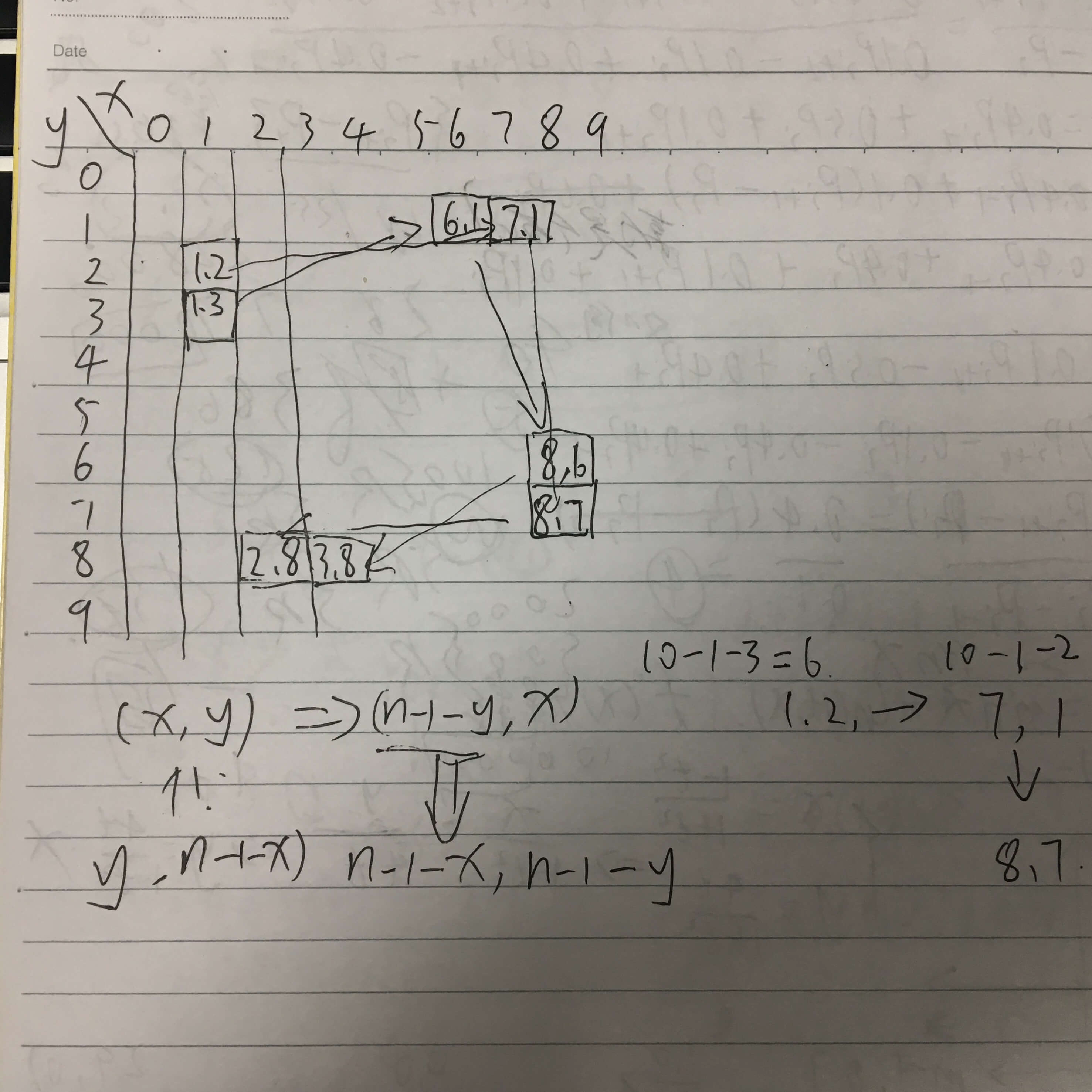
所以说,点(x,y) 移动到了点(n-1-y,x) 的位置,以此类推。。。
所以说,就得出了结果
成绩

代码
class Solution:
def rotate(self, matrix):
"""
:type matrix: List[List[int]]
:rtype: void Do not return anything, modify matrix in-place instead.
"""
n = len(matrix)
x,y = 0,0
border = n//2+n % 2
flag = n%2
# print(border)
for x in range(border):
for y in range(border):
# print(matrix[y][x])
if flag == 1 and x == border-1:
continue
t = matrix[y][x]
matrix[y][x] = matrix[n-1-x][y]
matrix[n-1-x][y] = matrix[n-1-y][n-1-x]
matrix[n-1-y][n-1-x] = matrix[x][n-1-y]
matrix[x][n-1-y] = t
# matrix = [
# [5, 1, 9, 11],
# [2, 4, 8, 10],
# [13, 3, 6, 7],
# [15, 14, 12, 16]
# ]
matrix = [
[1, 2, 3],
[4, 5, 6],
[7, 8, 9]
]
for v in matrix:
print(v)
Solution().rotate(matrix)
print("result:")
for v in matrix:
print(v)
# 原地旋转输入矩阵,使其变为:
# [
# [15, 13, 2, 5],
# [14, 3, 4, 1],
# [12, 6, 8, 9],
# [16, 7, 10, 11]
# ]