03复杂度分析(上):如何分析、统计算法的执行效率和资源消耗?1. 只关注循环执行次数最多的一段代码时间复杂度表达的是

以下内容总结自极客时间王争大佬的《数据结构与算法之美》课程，本文章仅供个人学习总结。

为什么需要复杂度分析？

普通的测试一个算法运行的时间会收到很多因素的影响，比如一个i7处理器，一个i3处理器跑相同的代码，肯定i7更快。不同的输入得到的测试数据也不同，比如并不是所有的数据量用快速排序就会比插入排序快。所以我们需要去掉这些影响因素，得到一个相对公平的估算算法执行效率的方法。也就是时间、空间复杂度分析。

时间复杂度分析的方法

1. 只关注循环执行次数最多的一段代码

时间复杂度表达的是一种趋势，即随着输入的不同，代码运行时间的趋势是怎样的。所以我们通常会忽略掉常量和低阶系数，只需要关注最大阶的量级就可以了。所以分析算法复杂度的时候只需要关注循环执行次数最多的那一段代码就可以了。下面一个简单的例子。

function cal(n) {
    let sum = 0;
    for(let i = 1; i <= n; i++) {
        sum = sum + i;
    }
    return sum;
}

我们很容易看到循环最多的是第3、4行代码，所以对这块进行重点分析，这两行代码被执行了n次，所以总的时间复杂度就为O(n)

2. 加法法则：总复杂度等于量级最大的那段代码的复杂度

接下来看一个稍微多一点的代码，分析进行分析

function cal(n) {
    let sum_1 = 0;
    for (let p = 1; p < 100; p++) {
        sum_1 = sum_1 + p;
    }
    
    let sum_2 = 0;
    for(let q = 1; q < n; q++) {
        sum_2 = sum_2 + q;
    }
    
    let sum_3 = 0;
    for (let i = 0; i <= n; i++) {
        for (let j = 1; j < n; j++) {
            sum_3 = sum_3 + i + j;
        }
    }
    
    return sum_1 + sum_2 + sum_3;
}

代码分三部分，分别求 sum_1、sum_2、sum_3，我们一个一个分析。

求sum_1，循环了100次，因为100是个常量，和n没有任何关系。所以求sum_1的时间复杂度为O(1)

求sum_2，循环了n次，和n是有关系的，并且n是多少就循环多少次，所以求sum_2的时间复杂度为O(n)

求sum_3，看到有两个for循环，其中执行最多的代码有sum_3 = sum_3 + i + j;外层的for循环执行了n次，内层的for循环在每次外层循环一次时会执行n次，所以最多执行了n*n次。所以sum_3的时间复杂度为O(n^2)

整体的时间复杂度为 O(1)、O(n)、O(n^2)的最大值，即O(n^2)

3. 乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

function cal(n) {
    let ret = 0;
    for (let i = 1; i <= n; i++) {
        ret = ret + f(i);
    }
}
function f(n) {
    let sum = 0;
    for (let i = 0; i <= n; i++) {
        sum = sum + i;
    }
    return sum;
}

单独看cal()函数，假设f()是一个普通操作，那么cal()的时间复杂度就是O(n)，但是f()不是一个简单的操作，f()的时间复杂度也是O(n),并且f()是嵌套在cal()的循环中，所以cal()函数的时间复杂度为O(n) * O(n) = O(n^2)

几种常见的时间复杂度

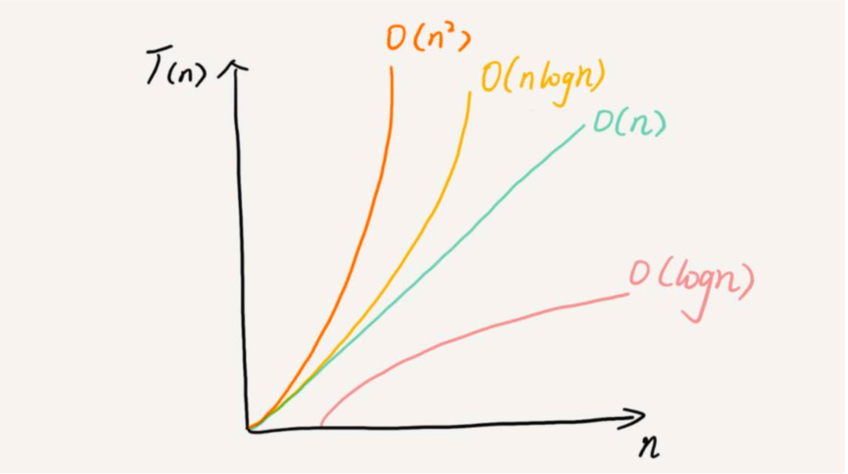
虽然代码千差万别，但是常见的复杂度也就那几种。按照复杂度的数量级进行排序如下：O(1)、O(logn)、O(n)、O(nlogn)、O(n^2)、O(n^3)、O(n^k)、O(2^n)、O(n!)

上面的几种复杂度量级可以分为两种，一种是多项式级别和非多项式级别，上面的复杂度量级中 O(2^n)和O(n!)就是非多项式级别，随着n的增长，执行时间会极具增加，所以讨论这两种基本上没多大意义。我们常见的一些复杂度其实就是几种多项式级别的复杂度。

O(1): 并不是只执行了一行代码，而是代码的执行时间不随着n的增长而增长，那么时间复杂度就是O(1)。下面举个例子：
```
function cal(n) {
    let sum = 0;
    for (let i = 1; i <= 10000; i++) {
        sum = sum + i + n;
    }
}
```
不管n多大，整个代码都是执行10000次，这个函数的时间复杂度就是O(1)。
O(logn)：这种的可能不大好直接说，我们直接上代码去分析
```
function cal(n) {
    let i = 1;
    while(i <= n) {
        i = i * 2;
    }
}
```
我们从代码中可以看到，i每次是乘2的，所以循环出来就是 2^1 2^2 2^3 ... 2^x = n，我们知道x的值是多少就知道运行了多少次，根据数学运算，x=log以2为底n的对数，所以时间复杂度为 $O(log_2^n)$

现在再改一下代码
```
function cal(n) {
    let i = 1;
    while(i <= n) {
        i = i * 3;
    }
}
```
和上面的一样的套路，那么时间复杂度就是 $O(log_3^n)$ ，实际上，不管是以2还是3或者10为底，我们都可以把所有对数阶的时间复杂度记为 $O(logn)$ ，因为根据数学中的对数运算来说 $log_3^n = log_3^2 * log_2^n$ 而 $log_3^2$ 又是一个常量，所以可以忽略掉，于是最后又成了 $log_2^n$ ，所以在对数阶的复杂度表示中，统一使用 $O(logn)$ 来表示时间复杂度。

同理，根据上面讲过的乘法法则，如果一段代码的时间复杂度为 $O(logn)$ ，我们循环执行n遍，那么时间复杂度就成了 $O(nlogn)$

O(m + n)、O(m * n)

functin cal(m, n) {
    let sum_1 = 0;
    for (let i = 0; i < m; i++) {
        sum_1 = sum_1 + i;
    }
    
    let sum_2 = 0;
    for (let j = 0; j < m; i++) {
        sum_2 = sum_2 + j;
    }
    
    return sum_1 + sum_2;
}

上面的代码，有两个输入，根据之前的标准，要找循环次数最多的代码作为时间复杂度，但是两个输入是不确定哪个大哪个小，无法忽略其中一个。所以整个代码的时间复杂度为O(m + n)

空间复杂度

前面的时间复杂度讲的是执行时间与数据规模之间的增长关系，空间复杂度则是算法的存储空间和数据规模之间的增长关系。

function fn(n) {
    let arr = new Array(n);
    for (let i = 0; i < n; i++) {
        arr[i] = i;
    }
}

上面的第二行代码我们创建了一个长度为n的数组，和创建了一个i变量，但是i变量是常量级别的，和n没有关系所以可以忽略。剩下的除了一个长度为n的数组没有占用其他的空间，所以整个代码的空间复杂度为O(n)。

我们常见的空间复杂度O(1)，O(n)，O(n^2) ,像 $O(logn)$ ， $O(nlogn)$ 这样的对数阶在空间复杂度中就基本上不会碰到。

内容小节

用一张图来表示各个复杂度随着数据量的增长趋势，让我们能更直观的感受到不同算法之间的性能差异。一些基本的算法基本上复杂度都是图上的这几个。在看代码的时候，多思考，也可以多想想自己现在写的代码时间空间复杂度是多少，是否能够降低，长此以往，能够大大提升自己的代码质量和代码性能。

课后思考

有人说，我们项目之前都会进行性能测试，再做代码的时间复杂度、空间复杂度分析，是不是多此一举呢?而且，每段代码都分析一下时间复杂度、空间复杂度，是不是很浪费时间呢?你怎么看待这个问题呢?

性能测试和做代码的时间空间复杂度进行分析并不冲突，在开发的时候就考虑到时间复杂度和空间复杂度，能够降低后期维护的成本，性能测试一般是在开发完毕后，如果测试结果不达标，再去返工，会有更大的成本。

并不是一定要对每一行代码进行时间空间复杂度分析，一个项目动辄几万代码，一行一行的分析是不切实际也是没必要的，开发人员有了时间空间复杂度意识之后，在某些需要注意的地方去刻意注意一下时间空间复杂度，能够让项目性能更好。比如前端做一些复杂动画之类的操作的时候，就需要注重观察时间空间复杂度，否则动画就会卡顿。重要的是知道在什么时候需要复杂度分析，而不是对全部代码进行复杂度分析或者直接忽略复杂度分析。