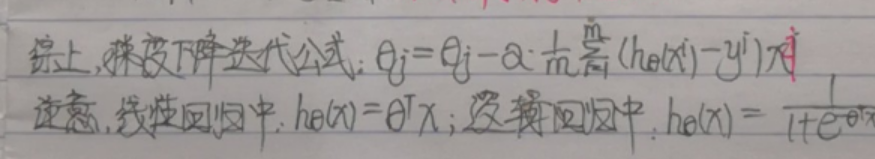逻辑回归公式推导

一、预测函数：

• 1.第一个式子称为sigmoid函数，先了解一下sigmoid函数：

  

  通过sigmoid函数与线性回归预测函数的联立，即可得到逻辑回归的预测函数

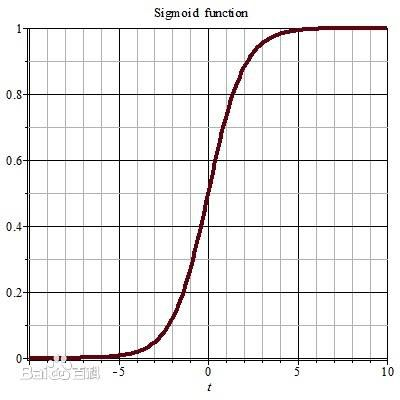
• 2.即是说，逻辑回归的预测函数实际上是：

  • ①通过线性回归的预测函数得到一个预测值（连续值）
  • ②接着把这个连续值丢进sigmoid函数得到一个概率值（0到1之间）
  • ③若概率值大于0.5，归为一类；若概率值小于0.5，归为一类（仅考虑二分类）

• 3.sigmoid函数的输出值解读：在输入值x和参数θ一定的前提下，y=1的概率，即：

• 4.由sigmoid函数的分类分界点为0.5可得出线性回归预测函数判定边界的概念：

二、代价函数：

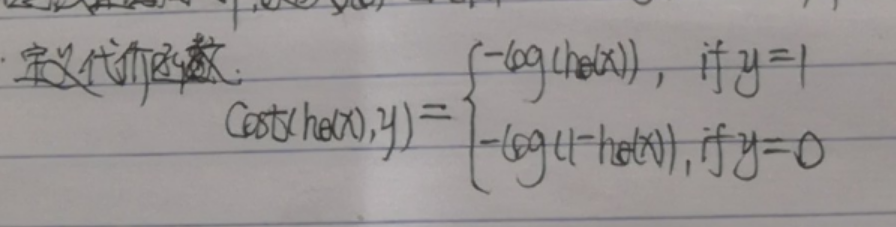
• 1.先说明这个代价函数的合理性及将其化为等价形式：

  

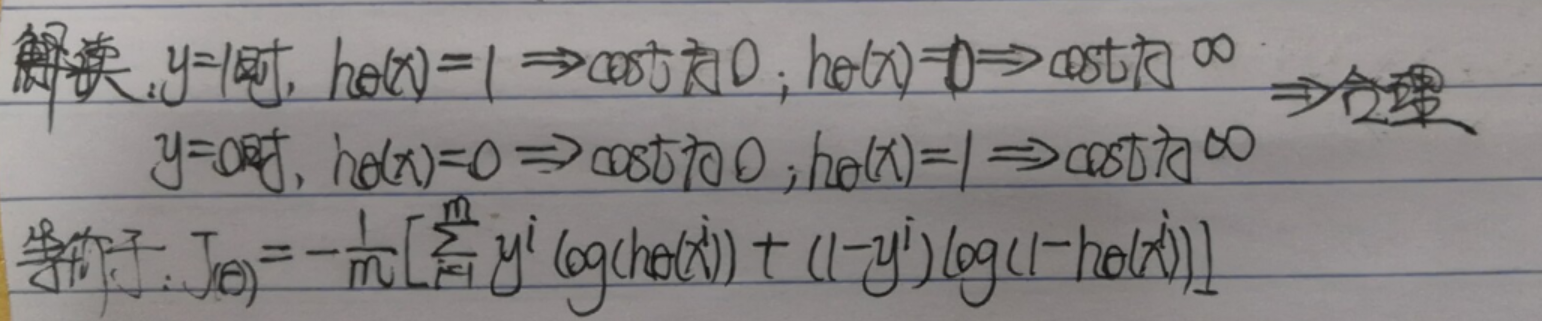
• 2.代价函数的推导（与线性回归类似，先用似然函数表示，再用对数求极大似然）：

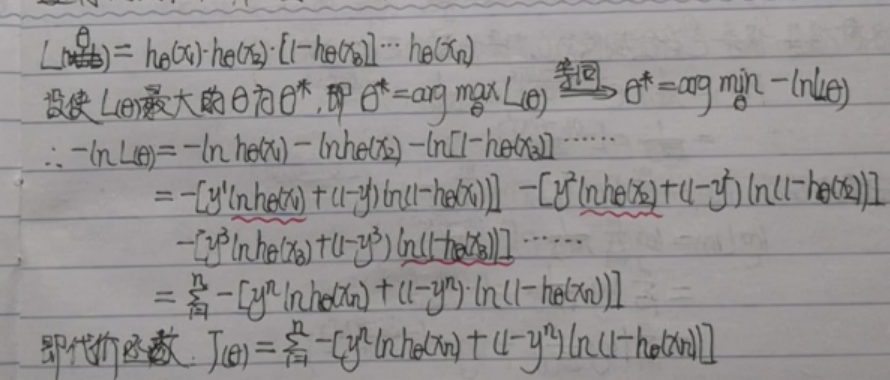
  • 假设x1属于类别1，x2属于类别1，x3属于类别0……xn属于类型1：

    

• 3.为什么不能继续使用线性回归的代价函数？

  

三、梯度下降：

• 1.先给出结论：

  

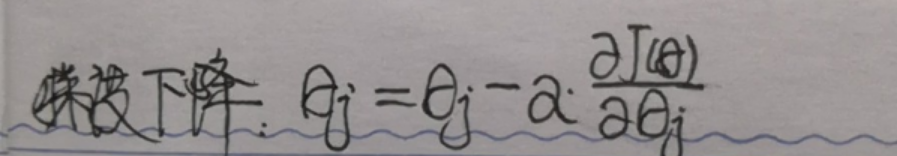
• 2.同之前的线性回归梯度下降，这里只要能求出后面的偏导数，问题即可解决，不过在此之前，先求一下sigmoid函数的导数，在后续求导中会用到：

  

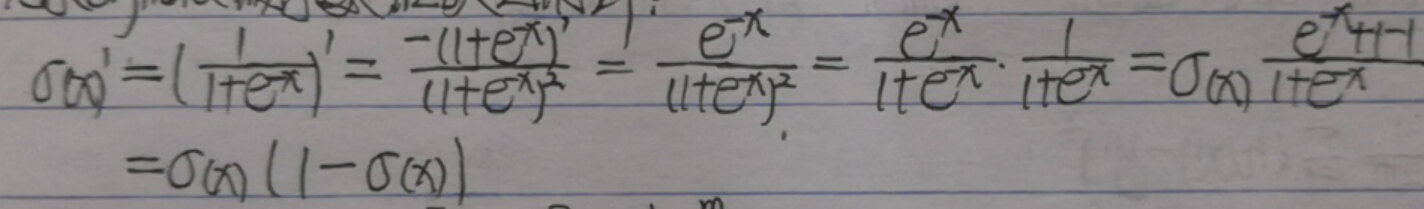
• 3.正式开始推导：

• 4.综上（注意逻辑回归和线性回归的梯度下降公式在形式上是一样的，但是预测函数不一样）：