机器学习中的核函数比如将x1和x2的超平面变为的高阶多项式函数。我们将映射函数设为 . 我们对一个二维空间做映射，选

本文参考:blog.pluskid.org/?p=685

核函数在SVM主要起到了两种作用

将数据从低维映射到高维，将原本线性不可分的情况变成了线性可分
降低计算级数

低维映射到高维

其中第一点的核心思想用几何来展示如下：

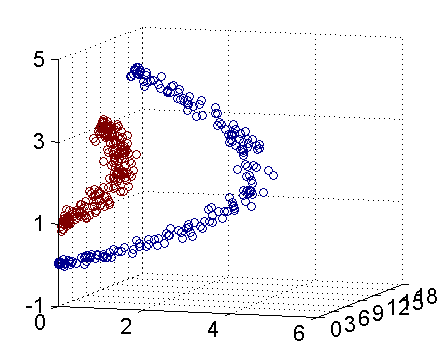
比如将x1和x2的超平面变为 $a_1X_1 + a_2X_1^2 + a_3 X_2 + a_4 X_2^2 + a_5 X_1X_2 + a_6 = 0$ 的高阶多项式函数。我们将映射函数设为 $\phi(\cdot)$ .

我们对一个二维空间做映射，选择的新空间是原始空间的所有一阶和二阶的组合，得到了五个维度；如果原始空间是三维，那么我们会得到 19 维的新空间（验算一下？），这个数目是呈爆炸性增长的，这给 ϕ(⋅) 的计算带来了非常大的困难，而且如果遇到无穷维的情况，就根本无从计算了。所以就需要 Kernel 出马了。

降低计算复杂度

其中第一点在线性回归中使用高阶多项式就能做到，所以核函数真正最重要的是降低计算复杂度。

所谓的核函数，其实是一种计算的技巧，所以又被称为 Kernel Trick 。

例如SVM中分类函数最终形式如下：

f(x) = \sum_{i=1}^n\alpha_i y_i \langle x_i, x\rangle + b

现在通过映射函数变为:

f(x) = \sum_{i=1}^n\alpha_i y_i \langle \phi(x_i), \phi(x)\rangle + b

其对偶问题：

\begin{align}
\max_\alpha &\sum_{i=1}^n\alpha_i – \frac{1}{2}\sum_{i,j=1}^n\alpha_i\alpha_jy_iy_j\langle \phi(x_i),\phi(x_j)\rangle \\
s.t., &\alpha_i\geq 0, i=1,\ldots,n \\
&\sum_{i=1}^n\alpha_iy_i = 0
\end{align}

如之前所提到，这是没有核函数的直接映射方式。这样的计算将会非常复杂。

设两个向量为 $x_1 = (\eta_1,\eta_2)^T$ 和 $x_2=(\xi_1,\xi_2)^T$ 。

\left(\langle x_1, x_2\rangle + 1\right)^2 = 2\eta_1\xi_1 + \eta_1^2\xi_1^2 + 2\eta_2\xi_2 + \eta_2^2\xi_2^2 + 2\eta_1\eta_2\xi_1\xi_2 + 1

这个式子可以理解为先做内积再做映射。

另外，我们又注意到：

\varphi(X_1,X_2)=(\sqrt{2}X_1,X_1^2,\sqrt{2}X_2,X_2^2,\sqrt{2}X_1X_2,1)^T

完全等价于这个式子先做映射再作内积 $<\varphi(x_1,x_2),\varphi(x_2,x_1)> = \left(\langle x_1, x_2\rangle + 1\right)^2$ 。

所以我们可以得到新的对偶问题公式:

\begin{align}
\max_\alpha &\sum_{i=1}^n\alpha_i – \frac{1}{2}\sum_{i,j=1}^n\alpha_i\alpha_jy_iy_j \color{red}{\kappa(x_i, x_j)} \\
s.t., &\alpha_i\geq 0, i=1,\ldots,n \\
&\sum_{i=1}^n\alpha_iy_i = 0
\end{align}

这将会大大降低计算复杂度。同时将低位数据隐式映射到高维度。

这里还有其他简单例子如下：

我们现在考虑核函数K，即“内积平方”。

这个核函数对应着一个二维空间到三维空间的映射，它的表达式是：

可以验证，

构造核函数

当然，因为我们这里的例子非常简单，所以我可以手工构造出对应于 φ(⋅) 的核函数出来，如果对于任意一个映射，想要构造出对应的核函数就很困难了。

最理想的情况下

我们希望知道数据的具体形状和分布
从而得到一个刚好可以将数据映射成线性可分的 ϕ(⋅)
然后通过这个 ϕ(⋅) 得出对应的 κ(⋅,⋅) 进行内积计算。

然而，第二步通常是非常困难甚至完全没法做的。不过，由于第一步也是几乎无法做到，因为对于任意的数据分析其形状找到合适的映射本身就不是什么容易的事情，所以，人们通常都是“胡乱”选择映射的，

所以，根本没有必要精确地找出对应于映射的那个核函数，而只需要“胡乱”选择一个核函数即可。 我们知道它对应了某个映射，虽然我们不知道这个映射具体是什么。由于我们的计算只需要核函数即可，所以我们也并不关心也没有必要求出所对应的映射的具体形式。

当然，说是“胡乱”选择，其实是夸张的说法，因为并不是任意的二元函数都可以作为核函数，所以除非某些特殊的应用中可能会构造一些特殊的核（例如用于文本分析的文本核，注意其实使用了 Kernel 进行计算之后，其实完全可以去掉原始空间是一个向量空间的假设了，只要核函数支持，原始数据可以是任意的“对象”——比如文本字符串），通常人们会从一些常用的核函数中选择（根据问题和数据的不同，选择不同的参数，实际上就是得到了不同的核函数），例如：