函数的渐近增长
假设两个算法的输入规模都是n,算法A要做2n+3次操作,你可以理解为先有一个n次的循环,执行完成后,再有一个n次循环,最后有三次赋值或运算,共2n+3次操作。算法B要做3n+1次操作。
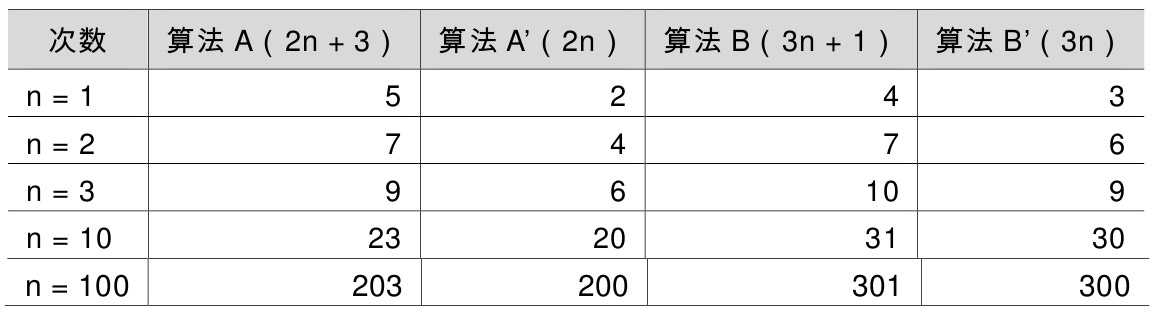
当n=1时,算法A效率不如算法B(次数比算法B要多一次)。而当n=2时,两者效率相同;当n>2时,算法A就开始优于算法B了,随着n的增加,算法A比算法B越来越好了(执行的次数比B要少)。于是我们可以得出结论,算法A总体上要好过算法B。
输入规模n在没有限制的情况下,只要超过一个数值N,这个函数就总是大于另一个函数,函数是渐近增长的。
函数的渐近增长:给定两个函数f(n)和g(n),如果存在一个整数N,使得对于所有的n>N,f(n)总是比g(n)大,那么,我们说f(n)的增长渐近快于g(n)。
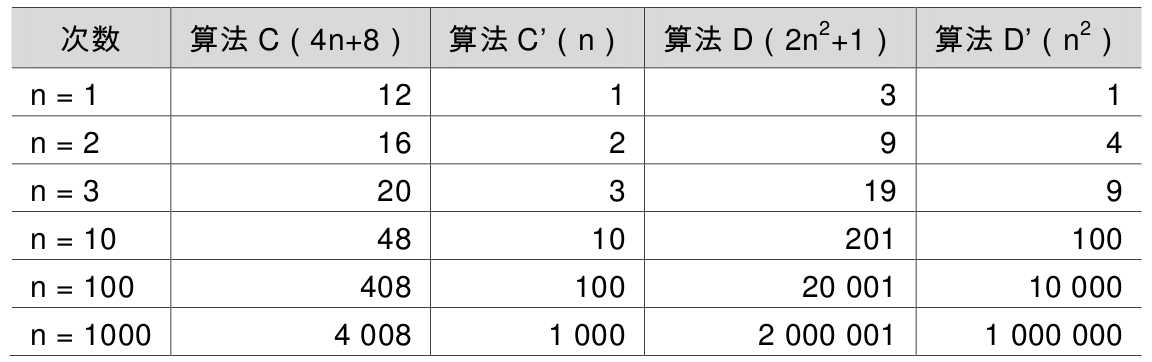
当n≤3的时候,算法C要差于算法D(因为算法C次数比较多),但当n>3后,算法C的优势就越来越优于算法D了,到后来更是远远胜过。
而当后面的常数去掉后,其实结果没有发生改变。
去掉与n相乘的常数,这样的结果也没发生改变,算法C′的次数随着n的增长,还是远小于算法D′。也就是说,与最高次项相乘的常数并不重要。
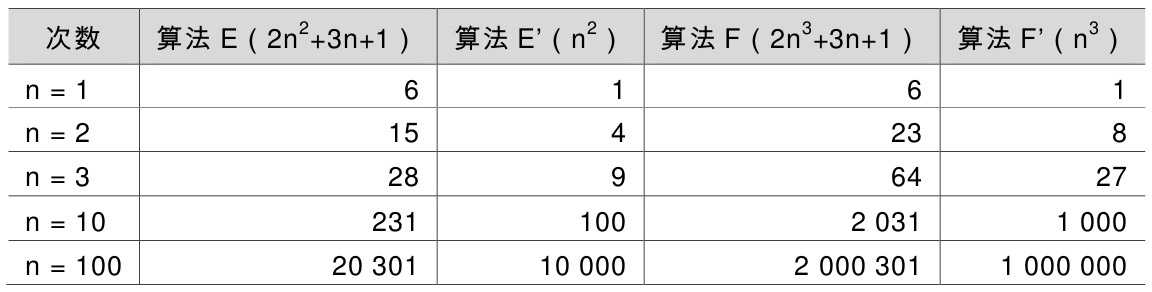
当n=1的时候,算法E与算法F结果相同,但当n>1后,算法E的优势就要开始优于算法F,随着n的增大,差异非常明显。通过观察发现,最高次项的指数大的,函数随着n的增长,结果也会变得增长特别快。
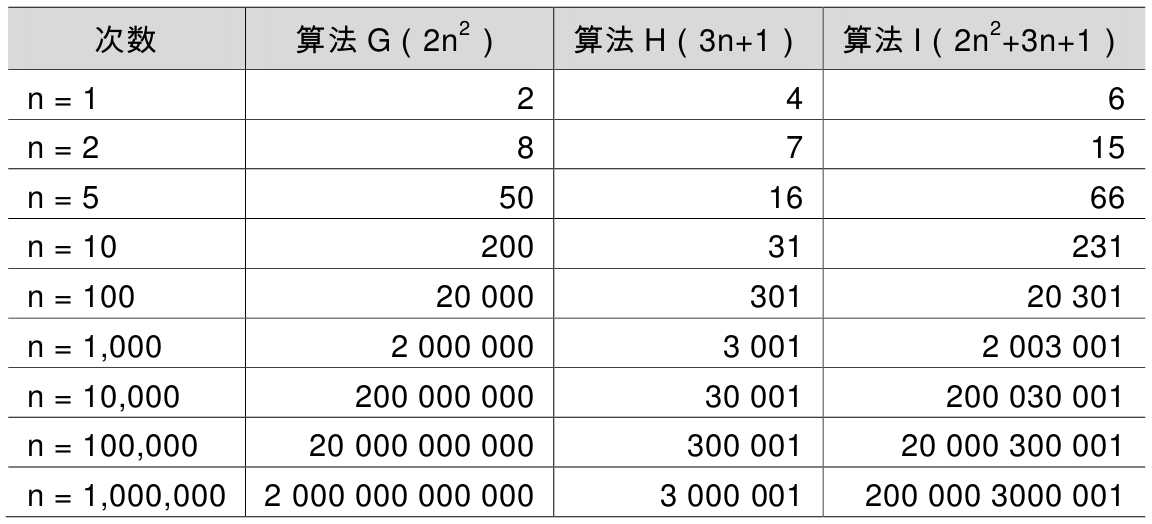
当n的值越来越大时,你会发现,3n+1已经没法和2n2的结果相比较,最终几乎可以忽略不计。也就是说,随着n值变得非常大以后,算法G其实已经很趋近于算法I。于是我们可以得到这样一个结论,判断一个算法的效率时,函数中的常数和其他次要项常常可以忽略,而更应该关注主项(最高阶项)的阶数。
如果对比这几个算法的关键执行次数函数的渐近增长性,可以分析出:某个算法,随着n的增大,它会越来越优于另一算法,或者越来越差于另一算法。这其实就是事前估算方法的理论依据,通过算法时间复杂度来估算算法时间效率。
欢迎扫描下方二维码,持续关注:

互联网工程师(id:phpstcn),我们一起学习,一起进步