7种排序算法

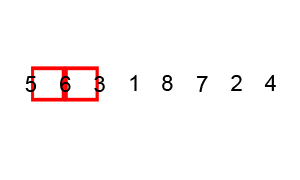
冒泡排序

自上而下对相邻的两个数依次进行比较和调整，让较大的数往下沉，较小的往上冒。即：每当两相邻的数比较后发现它们的排序与排序要求相反时，就将它们互换。

function BubbleSort(originalArray) {
  // Flag that holds info about whether the swap has occur or not.
  let swapped = false;
  // Clone original array to prevent its modification.
  const array = [...originalArray];

  for (let i = 1; i < array.length; i += 1) {
    swapped = false;

    for (let j = 0; j < array.length - i; j += 1) {

      // Swap elements if they are in wrong order.
      if (array[j + 1] < array[j]) {
        const tmp = array[j + 1];
        array[j + 1] = array[j];
        array[j] = tmp;

        // Register the swap.
        swapped = true;
      }
    }

    // If there were no swaps then array is already sorted and there is
    // no need to proceed.
    if (!swapped) {
      return array;
    }
  }

  return array;
}

选择排序

在要排序的一组数中，选出最小的一个数与第一个位置的数交换；然后在剩下的数当中再找最小的与第二个位置的数交换，如此循环到倒数第二个数和最后一个数比较为止。

function selectionSort(originalArray) {
  const array = [...originalArray];

  for (let i = 0; i < array.length; i += 1) {
    let minIndex = i;
    for (let j = i + 1; j < array.length; j += 1 ) {
      if (array[j] < array[minIndex]) {
        minIndex = j;
      }
    }
    // If new minimum element has been found then swap it with current i-th element.
    if (minIndex !== i) {
      const tmp = array[i];
      array[i] = array[minIndex];
      array[minIndex] = tmp;
    }
  }
  return array;
}

插入排序

在要排序的一组数中，假设前面(n-1) [n>=2] 个数已经是排好顺序的，现在要把第n个数插到前面的有序数中，使得这n个数也是排好顺序的。如此反复循环，直到全部排好顺序。

function insertionSort(originalArray) {
  const array = [...originalArray];

  // Go through all array elements...
  for (let i = 0; i < array.length; i += 1) {
    let currentIndex = i;

    // Go and check if previous elements and greater then current one.
    // If this is the case then swap that elements.
    while (
      array[currentIndex - 1] !== undefined
      && (array[currentIndex] < array[currentIndex - 1])
    ) {
      // Swap the elements.
      const tmp = array[currentIndex - 1];
      array[currentIndex - 1] = array[currentIndex];
      array[currentIndex] = tmp;

      // Shift current index left.
      currentIndex -= 1;
    }
  }

  return array;
}

堆排序

堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。如下图：

小顶堆 与 大顶堆

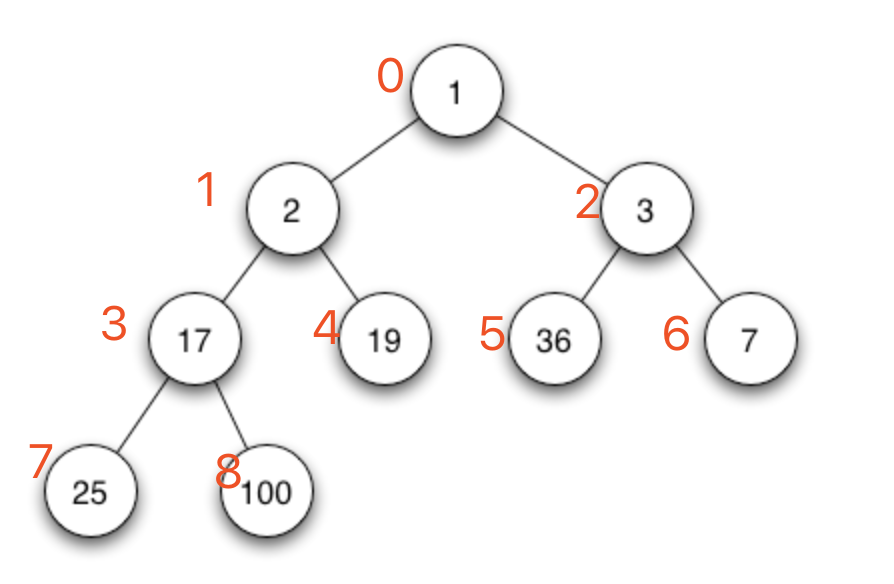
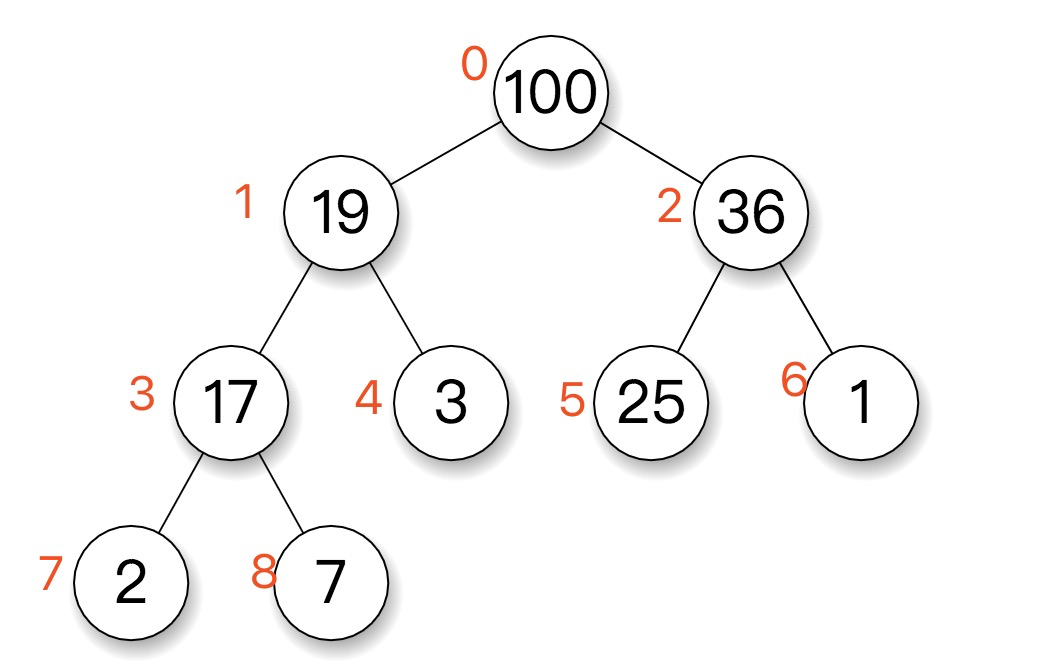
对应的数组为：[100, 19, 26, 17, 3, 25, 1, 2, 7] 该数组从逻辑上讲就是一个堆结构，我们用简单的公式来描述一下堆的定义就是： __大顶堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]  __ __小顶堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]  __

堆排序原理的动画：

// 重新调整为大顶堆
function heapify(arr, size, index) {
  let largest = index; // 父级节点
  const left = 2 * index + 1;
  const right = 2 * index + 2;
  if (left < size && arr[left] > arr[largest]) {
      largest = left;
  }
  if (right < size && arr[right] > arr[largest]) {
      largest = right;
  }
  if (largest !== index) {
    swap(arr, index, largest);
    heapify(arr, size, largest);
  }
}
function swap(a, i, j) {
  let tmp = a[i];
  a[i] = a[j];
  a[j] = tmp;
}
//这里的堆排序用的是最大堆
function heapSort(originalArray) {
  const arr = [...originalArray];
  const size = arr.length;
  // 建立大顶堆
  // Math.floor(size / 2 - 1) 为父级节点index
  for (let i = Math.floor(size / 2 - 1); i >= 0; i--) {
    heapify(arr, size, i);
  }
  for (let i = size - 1; i >= 0; i--) {
    // 将堆顶元素与末尾元素进行交换，使末尾元素最大
    swap(arr, 0, i);
    // 重新调整为大顶堆,直到整个堆序列有序。
    heapify(arr, i, 0);
  }
  return arr;
}

归并排序

归并排序应用递归来把数组分解成左右两半的一个小数组，直到这个小数组被拆分成的元素个数<=1;然后再将小数组两两合并而成有序的大数组。这里面就是应用到分治策略。

function mergeSort(arr) {
  if (arr.length <= 1) {
    return arr;
  }
  // 将数组拆分两半
  let midleIndex =  Math.floor(arr.length / 2);
  let leftArray = arr.slice(0, midleIndex);
  let rightArray = arr.slice(midleIndex, arr.length);
  // 递归，将左右两边的继续拆，直到每个数组的length <= 1;
  let leftSortedArray = mergeSort(leftArray);
  let rightSortedArray = mergeSort(rightArray);
  return mergeArrays(leftSortedArray, rightSortedArray);
}

// 对拆分的数组比较后合并
function mergeArrays(leftArray, rightArray) {
  let sortedArray = [];
  while (leftArray.length && rightArray.length) {
    let minNumElement = null;
    // 找左右两边数组最小的那个
    if (leftArray[0] <= rightArray[0]) {
      minNumElement = leftArray.shift();
    } else {
      minNumElement = rightArray.shift();
    }
    // push到空数组
    sortedArray.push(minNumElement);
  }
  if (leftArray.length) {
    sortedArray = sortedArray.concat(leftArray);
  }
  if (rightArray.length) {
    sortedArray = sortedArray.concat(rightArray);
  }
  return sortedArray;
}

快速排序

• 在数组中找到一个基准数（pivot）
• 分区，将数组中比基准数大的放到它的右边，比基准数小的放到它的左边
• 继续对左右区间重复第二步，直到各个区间只有一个数，这时候，数组也就有序了。

function quickSort(sourceArray) {
  const arr = [...sourceArray];
  if(arr.length <= 1) {
    return arr;
  }
  // 初始化中间元素左右两边数组
  const leftArray = [];
  const rightArray = [];
  // 将第一个元素作为基准
  const pivotElement = arr.shift();
  const centerArray = [pivotElement];
  // 每个元素与基准值比较，分别放在左、中、右数组
  while(arr.length > 0) {
    const currentElement = arr.shift();
    if (currentElement === pivotElement) {
      centerArray.push(currentElement);
    } else if (currentElement < pivotElement) {
      leftArray.push(currentElement);
    } else {
      rightArray.push(currentElement);
    }
  }
  // 对左右的数组递归排序
  const leftSortedArray = quickSort(leftArray);
  const rightSortedArray = quickSort(rightArray);
  // 最后将排好序的数组合并
  return leftSortedArray.concat(centerArray, rightSortedArray);
}

希尔排序

首先取 gap = Math.floor(arr.length / 2), 将数组分为 4 组，如下图中相同颜色代表一组：

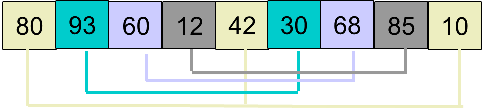
然后分别对 4 个小组进行插入排序，排序后的结果为：

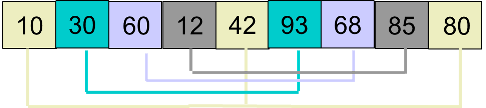
然后，取gap = Math.floor(gap / 2)，将原数组分为 2 小组，如下图：

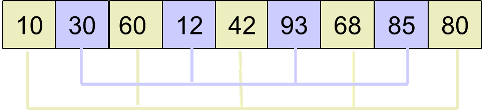
然后分别对 2 个小组进行插入排序，排序后的结果为：

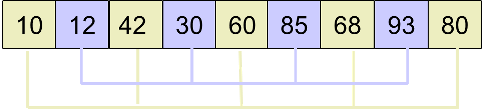
最后，取 d~3~ = 1，进行插入排序后得到最终结果：

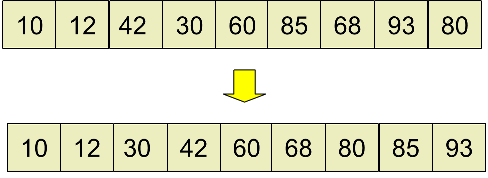
function shellSort(originArray) {
  const arr = [...originArray];
  // 定义基准间隔
  let gap = Math.floor(arr.length / 2);
  while (gap > 0) {
    // 循环所有间距的元素
    for(let i = 0; i < (arr.length - gap); i += 1) {
      let currentIndex = i;
      let gapShiftedIndex = i + gap;
      console.log(gap);
      while (currentIndex >= 0) {
        // 比较交换数组
        if(arr[gapShiftedIndex] < arr[currentIndex]) {
          let tmp = arr[currentIndex];
          arr[currentIndex] = arr[gapShiftedIndex];
          arr[gapShiftedIndex] = tmp;
        }
        gapShiftedIndex = currentIndex;
        currentIndex -= gap;
      }
    }
    gap = Math.floor(gap / 2);
  }
  return arr;
}

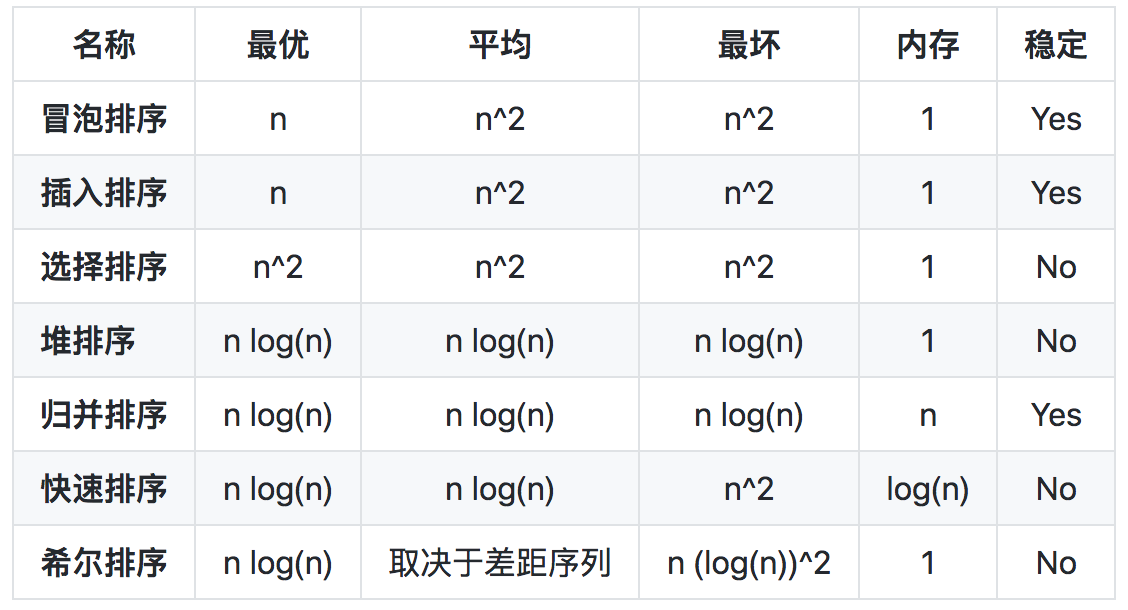
附：7种数组排序算法的复杂度：