周围有一些朋友总说:“面试时候看到红黑树真的头大!各种情况太难记了。”确实,如果仅仅想通过记忆来搞定红黑树那确实有点难度的,但是如果理解的话,红黑树其实很简单,所以我就分享一下我对红黑树的理解。
1.简单复习下红黑树的规则。
- 节点必须是红色或者黑色。
- 根节点必须是黑色。
- 叶节点(NIL)是黑色的。(NIL节点无数据,是空节点)
- 不能出现连续两个红色节点。
- 从任一节点出发到其每个叶子节点的路径,黑色节点的数量是相等的。
2.先讲解一波操作,后面再给出论证
插入操作如下,
- 每次插入第一步,将新插入节点设置为红色。
- 每次插入最后一步,将根节点设置为黑色。
- 当且仅当新插入节点的父节点为红色时,重新调整红黑树的平衡(调整步骤如下)。
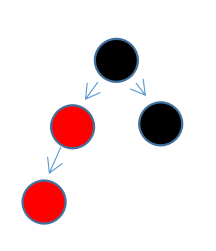
第一种:新插入节点 父节点的 兄弟节点 为黑色(左下角节点为新插入节点)
第二种:新插入节点 父节点的 兄弟节点 为红色(左下角节点为新插入节点)
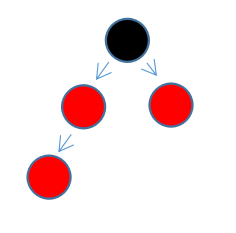
两种情况逐个分析。
在第一种情况下,想要恢复树的平衡,只需要将连续的两个红色节点,分一个给另外一个分支即可。这样的话,如果原来的树是平衡的,新树也必然平衡(两个分支的黑色节点数量并未变化)。
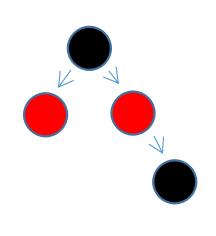
当然说是一回事,做是另一回事。下面就看看实际情况下,如何操作。
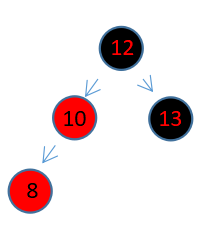
原树已经有12,10 ,13三个元素,新插入了一个8节点,此时,8与其父节点10都为红色,需要调整。将10设置为黑色,将12设置为红色,然后对节点12进行左旋操作(其实就是把8,10,12这三个顺序节点,重新以中间值10为中心在排一下)。
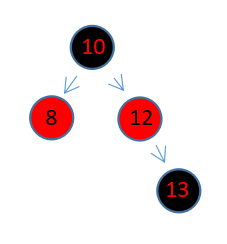
如果新插入的节点是11那该怎么办呢。
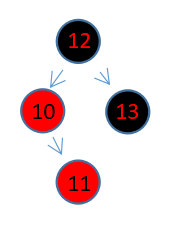
此时需要重排的三个节点为12,10,11,但是中间值11在最下面,直接重排不方便。所以需要多一步操作,对10节点进行右旋操作。
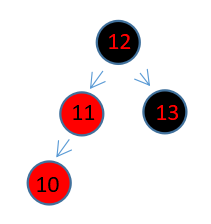
这样12 ,11 ,10 这三个节点也是顺序排列了。下一步操作就同上。如果从右边插入的话,操作也一样,镜像一下就ok。
现在再分析第二种情况(左下角为新插入节点)。
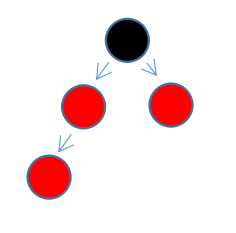
这种情况处理起来更简单,只需要将新插入节点的父节点,以及父节点的兄弟节点一起变成黑色,然后将爷爷节点变红即可(两个分支的黑色节点数量依然没有变化)。
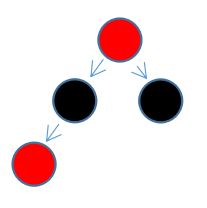
因为从爷爷节点往下,每个分支原来是一个黑色节点,现在依然是一个黑色节点,所以树还是平衡的,但是需要注意的是,因为爷爷节点由黑变红了。所以还得以爷爷节点为基准,迭代向上判断。直到爷爷节点的父节点为黑色或者爷爷节点为根节点为止。至于迭代中可能的情况,也无非就是我们列出来的这两种,参照一下即可。
3.最后论证插入操作的合理性:
红黑树规则:
- 节点必须是红色或者黑色。
- 根节点必须是黑色。
- 叶节点(NIL)是黑色的。(NIL节点无数据,是空节点)
- 不能出现连续两个红色节点。
- 从任一节点出发到其每个叶子节点的路径,黑色节点的数量是相等的。
- 每次插入第一步,将新插入节点设置为红色。
- 每次插入最后一步,将根节点设置为黑色。
- 当且仅当新插入节点的父节点为红色时,重新调整红黑树的平衡
首先,每次插入的第一步将插入节点设置为红色,因为如果树原本是平衡的话,插入一个红色节点并不会影响到规则5(从任一节点出发到其每个叶子节点的路径,黑色节点的数量是相等的)。
其次,在插入最后一步将根节点设置为黑色,这样规则2(根节点必须是黑色)就永远满足。
最后依据插入操作3(当且仅当新插入节点的父节点为红色时,重新调整红黑树的平衡),以及调整步骤,每次调整过后,都可以保证规则4(不能出现连续两个红色节点)也是可以满足的。
这样一来,只要严格遵循插入的这3条操作,就可以严格的保证红黑树的平衡了。或许你会问刚开始的第一条论证有一个前提条件“树原本是平衡的话”,如果这个前提条件不满足怎么办?
其实当你插入第一个根节点时,树已经处于了平衡的状态。所以只要一开始就遵循插入操作,根本就不会存在树不平衡的情况。所以这个插入操作是合理的。
下一篇:红黑树的删除操作