攻无不克,“栈”无不胜。
知彼知己,百“栈”不殆。
本文分享了一下栈的实现原理,以及一个简单的应用场景-简易计算器。
所有源码均已上传至github:链接
基于数组实现的顺序栈
1.首先需要初始化数组,申请一个大小为capacity的内存空间
public ArrayStack(int capacity) {
arrays = new int[capacity];
size = capacity;
count = 0;
}2.入栈
public boolean push(int num) {
// 这里当数组空间不够时,入栈失败,暂不扩容
if (count == size)
return false;
arrays[count] = num;
++count;
return true;
}3.出栈
public int pop() {
// 栈空
if (count == 0)
return -1;//-1表示没有数据
int res = arrays[count - 1];
--count;
return res;
}4.测试结果
ps:按数字大小顺序压栈
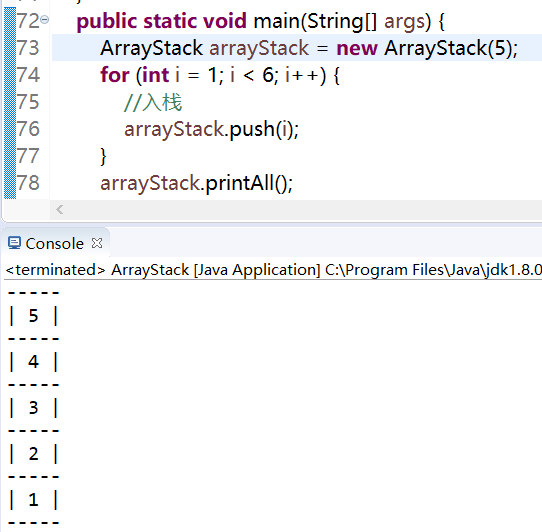
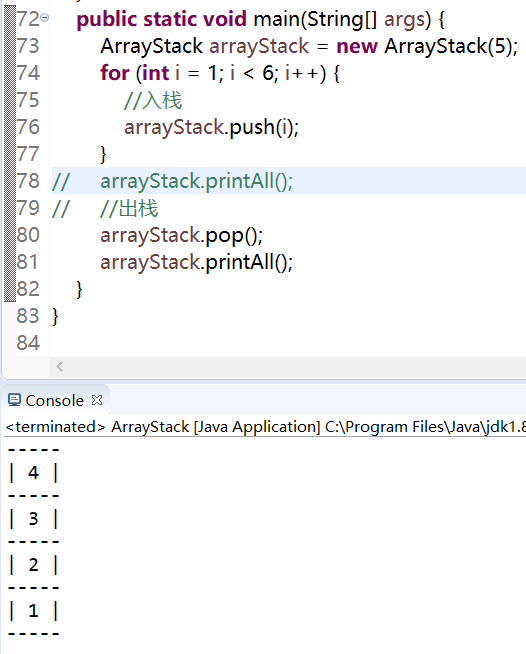
基于链表实现链式栈
链式栈则不需要像数组呢样在重载的构造方法初始化,直接声明即可
1.入栈
public void push(int num) {
Node node = new Node(num, null);
if (head != null) {
// 倒序插入,为出栈做准备
node.next = head;
}
head = node;
}2.出栈
public int pop() {
if (head == null)
return -1;// -1表示栈空
int res = head.data;
head = head.next;
return res;
}3.测试结果(与顺序栈保持一致)
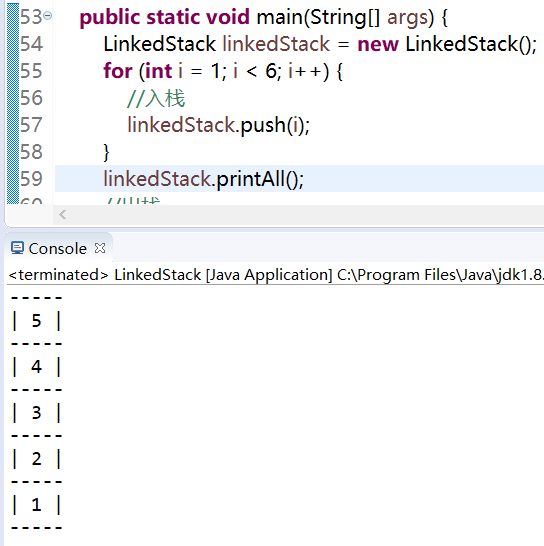
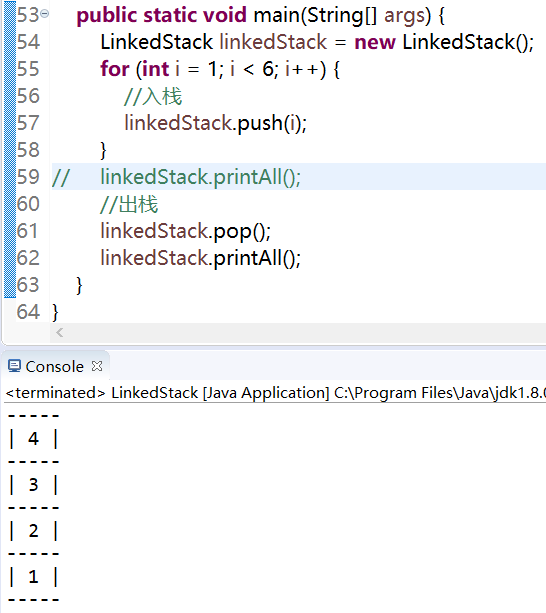
应用场景之简易计算器
分析
本次基于栈的简易计算器仅包含加减乘除等四则元素,比如计算 7-1+2*3+12/2。对于这个运算来讲 ,只是就是一个表达式求值的过程,对人来讲,口算都能算出来,可是对计算机来讲,这个表达式很难理解,具体应该怎么实现呢?
规则:这里和常规数学运算符一样,先乘除后加减,不包含括号,输入值为正整数。
具体实现如下
1.我们可以把该运算通过声明两个栈来实现。一个栈valStack用来保存值,一个栈calStack用来保存运算符。
process中的for循环从左往右依次遍历,当遇到数字的时候入栈valStack,遇到运算符的时候,先别忙入栈calStack,要先与栈B的栈顶元素进行比较,如果比栈顶元素优先级高,则入栈calStack,如果优先级低或者相同,则从栈valStack里取两个值,然后进行计算,再压入栈valStack。
当for循环执行完毕的时候,valStack栈的值的数量应该是比calStack的值得数量多一。
在while循环里将剩余的操作做完,直到一方为空。
最后清空栈即可。
public void process(String str) {
// 这里不做非空检验,默认传入的值一定正确有效
String[] strs = str.split(" ");
for (int i = 0; i < strs.length; i++) {
if (isNumber(strs[i])) {// 数字
valStack.push(Integer.valueOf(strs[i]));
} else {// 运算符
calDeal(strs[i]);
}
print();
}
while (!valStack.isEmpty() && !calStack.isEmpty()) {
String cal = calStack.pop();
Integer fInteger = valStack.pop();
Integer sInteger = valStack.pop();
result = calulate(cal, sInteger, fInteger);
valStack.push(result);
print();
}
valStack.clear();
calStack.clear();
}2.该方法就是当遇到操作符时开始判断是入栈还是计算
private void calDeal(String opt) {
//出栈
String calStar;
if (!calStack.isEmpty()) {
while (!calStack.isEmpty()) {
calStar = calStack.pop();
if (!compareOperator(opt, calStar)) {
Integer p = valStack.pop();
Integer q = valStack.pop();
result = calulate(calStar, q, p);
valStack.push(result);
}else {
calStack.push(calStar);
calStack.push(opt);
break;
}
}
}
if (calStack.isEmpty()) {
calStack.push(opt);
}
}3.计算方法
private Integer calulate(String opt, Integer p, Integer q) {
switch (opt) {
case "+":
return p + q;
case "-":
return p - q;
case "*":
return p * q;
case "/":
return p / q;
default:
break;
}
return null;
}4.比较操作符的优先级
private boolean compareOperator(String curCal, String tarCal) {
switch (tarCal) {
case "+":
case "-":
if ("-".equals(curCal) || "+".equals(curCal)) {
return false;
}
return true;
case "*":
case "/":
return false;
default:
break;
}
return true;
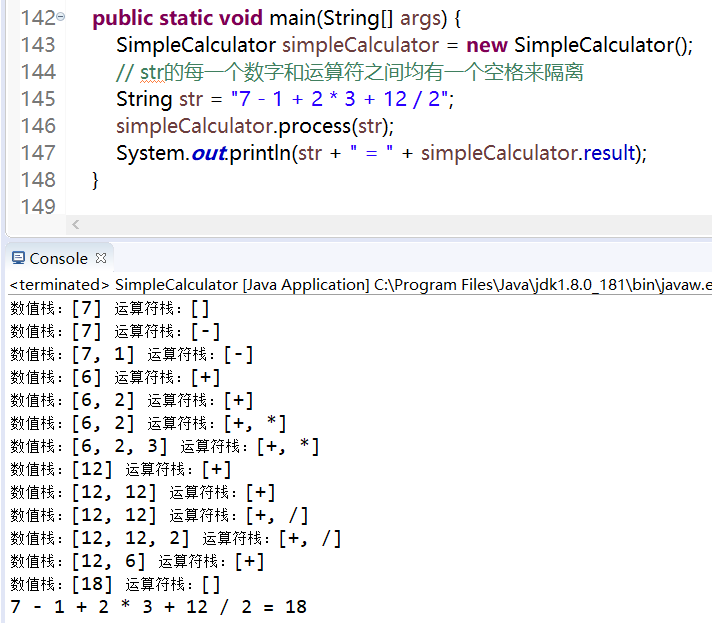
}测试结果
ps:该测试结果同时也将两个栈的变化打印出来,一目了然
扩展
下一篇则关于队列的具体实现和解析。
end
您的点赞和关注是对我最大的支持,谢谢!