VAE 的细节：p(x|z) 的噪音，与 p(z|x) 的编码坍塌变分自编码器 VAE 的常见错误理解，是认为 VAE

变分自编码器 VAE 的常见错误理解，是认为 VAE 模糊。

实际 VAE 不模糊，真正的 VAE 输出 p(x|z) 有很多噪音（由于常用的 Gaussian 模型是每点独立，因此噪音也是每点独立的噪音）。

许多论文显示的模糊图像，是 Gaussian 情况下的"平均图像" $\mathrm{E}[p(x|z)]$ ，并非真正的输出采样 $\tilde{x} \sim p(x|z)$ 。

这在 VAE 的推导中很清楚，例如本专栏之前的介绍：

PENG Bo：快速推导 VAE 变分自编码器，多种写法，和常见错误 Variational Autoencoderzhuanlan.zhihu.com

如下所述：

Vanilla VAEs with Gaussian posteriors / priors and factorized pixel distributions aren't blurry, they're noisy. People tend to show the mean value of p(x|z) rather than drawing samples from it. Hence the reported blurry samples aren't actually samples from the model, and they don't reveal the extent to which variability is captured by pixel noise. Real samples would typically demonstrate salt and pepper noise due to independent samples from the pixel distributions.

VAEs are poor models of data whenever insufficiently flexible posterior / prior / decoder distributions are used. These issues are much improved when more expressive choices are used as in IAF, pixelvae, variational lossy autoencoder.

我的观点，两全其美的方法，是用 VAE 生成图像的分布，再用 GAN 从中采样（降噪），以同时解决 GAN 的模式缺失，和 VAE 的噪音。关于图像分布，之前的实验：

PENG Bo：DGN v2：生成器应该输出分布，清晰图像并不是 GAN 的特权zhuanlan.zhihu.com

我用一个例子，说明 VAE 的噪音问题，以及编码坍塌。

这里的目标，是学会 $x \sim N(0, t^2)$ 。这可谓是最简单的任务。

然而，如果了解 VAE，会意识到，常见的 VAE 是学不会这个的。

令 E 网络输入的输出为 $\{\mu_x, \sigma_x^2\}$ 。

为得到解析解，不妨令 $\mu_x = a \cdot x$ ， $\sigma_x = b$ ，其中和是待训练的参数。

那么对应的编码是 $z \sim N(\mu_x, \sigma_x^2)$ 。

令 G 网络的输出为 $G(z) = c \cdot z$ ，其中是待训练的参数。

如果 t=1 ， a=1 ， b=0 ， c=1 ，那么 E 和 G 对于的还原是完美的，而且的实际分布 p(z) 也是完美的 N(0,1) 。

但是，常见的 VAE 不能看到，它只能看到，此时 E 网络的输出是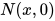，与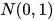相差甚远，于是 KL 散度会将它推过去，令还原变差。

在常见的 VAE 中，LOSS 为：

$\mathop{\arg\min}_{a,\, b,\, c} \mathbb{E}_{x \sim N(0,t^2)} \Big[ \mathbb{E}_{z \sim N(a \cdot x, b^2)} \vert c \cdot z - x \vert^2 + \beta \cdot \frac{1}{2} \sum_i \big(a^2x^2 + b^2 - \log b^2 -1 \big) \Big]$