机器学习之逻辑回归

2018-12-21 231 阅读3分钟

原文链接： stackbox.cn

逻辑回归用于解决分类问题

决策边界

sigmoid	z函数
$h(z) = \frac {1} {1 + e^{-z}}$	$z = \omega^{T} x + \omega_{0}$

此时函数y叫做sigmoid函数, 该函数可以将值分布在0和1之间, h(z)是一个条件概率

举例肿瘤数据集合有多个特征，假设恶性肿瘤概率 h(z) = 0.7, 也就是说

h(z)=p(y=1|x;ω;ω0)

翻译成人话就是在条件 $x;\omega;\omega_{0}$ 下为恶性肿瘤的概率为0.7, 其中 $x$ 为特征向量, $\omega$ 为权重向量, $\omega_{0}$ 为bias

而所谓的决策边界就是个线/面, 能分开函数z的输入集合, 假设有两个特征
$x_1$ $x_2$ , 分类数为2, 分别用圆圈和红叉表示, 可画成下面的图

线性决策额边界	非线性决策边界
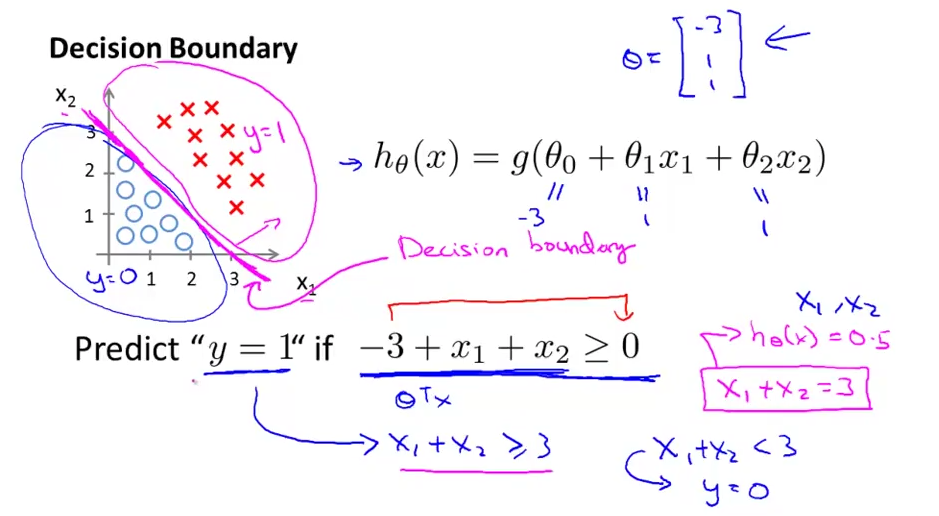image	image

损失函数

如果使用线性回归的那种均方差做损失函数, 不是一个凸函数, 这样就无法梯度下降求最优解了, 应该采用另外一种方式

均方差做损失函数	图形
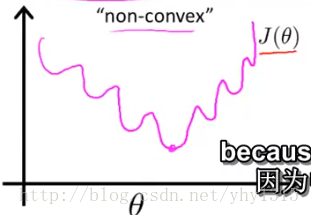$Loss = \frac {1} {2m} \sum_{i=1}^{m}(y_{i} - \frac {1} {1 + e^{-\omega^{T}x}})^2$	image

假设只有两个标签1 / 0, 即 $y_n \in {0,1}$ , 我们把采集的任意一组样本看作一个时间的话, 它发生的概率为 $p$ , 即模型y值等于标签1的概率为 p

Py=1=11+e−wTx
由于标签值不是就是0, 那么 $P_{y=0} = 1 -p$

上面的两个公式等价于:

P(yi|xi)=pyi(1−p)1−yi
意义为: 对于样本 $(x_i, y_i)$ , 对于 $x_i$ 这组数据，它的标签是 $y_i$ 的概率是 $p^{y_i}(1-p)^{1-y_i}$

那么假如有一组数据 ${ (x_1, y_1),(x_2, y_2),(x_3, y_3)…(x_n, y_n) }$ 这个合成的总事件发生的改率即每个样本发生概率的乘积

Ptotal=P(y1|xx)P(y2|x2)P(y3|x3)…P(yn|xn)=n∏i=1pyi(1−p)1−yi

我们的目标就是求合适的参数使得 $P_{total}$ 最大, 由于连乘不好算, 而且观察公式发现其函数值正比于其对数, 有以下公式

F(ω)=ln(Ptotal)=ln(n∏i=1pyi(1−p)1−yi)=n∑i=1ln(pyi(1−p)1−yi)=n∑i=1(yiln(p)+(1−yi)ln(1−p))

最后问题就变成了找到一个 $w^{*}$ , 使得 $F(\omega)$ 最大, 也就是使得 $-F(\omega)$ 最小, 数学上表达为

ω∗=argmaxωF(ω)

即 ω∗=−argminωF(ω)

梯度下降

首先对 $p$ 求导数, 结合sigmoid函数的性质, 其对向量 $\omega$ 的导数为 $p’ = p(1-p)x$

求损失函数的偏导数

∇F(ω)=∇(n∑i=1(yiln(p)+(1−yi)ln(1−p)))=n∑i=1(yiln′(p)+(1−yi)ln′(1−p))=n∑i=1(yi1pp′+(1−yi)11−p(1−p)′)=n∑i=1(yi1pp(1−p)xi−(1−yi)11−pp(1−p)xi)=n∑i=1(yi(1−p)xi−(1−yi)pxi)=n∑i=1(yi−p)xi

在SGD中，只要能随机的选取一个样本 $(x_i, y_i)$ , 然后再把值乘以N, 就相当于获取梯度的无偏估计

所以参数的随机梯度下降的公式为

ωt+1=ωt+ηN(yi−11+e−ωTxi)

其中 $\eta N$ 为一个常量, 所以参数的更新公式最终为

ωt+1=ωt+η(yi−11+e−ωTxi)

代码实现

github.com/Tara-X/algo…

非线性分类

用kernel trick即可实现非线性分类

与SVM/感知机的区别

感知机模型将分离超平面对数据分割，寻找出所有错误的分类点，计算这些点到超平面的距离，使这一距离和最小化，也就是说感知机模型的最优化问题是使得错误分类点到超平面距离之和最小化。
逻辑斯蒂回归是将分离超平面作为sigmoid函数的自变量进行输入，获得了样本点被分为正例和反例的条件概率，然后用极大似然估计极大化这个后验概率分布，也就是说逻辑斯蒂回归模型的最优化问题是极大似然估计样本的后验概率分布。
支持向量机的最优化问题是最大化样本点到分离超平面的最小距离。

参考资料