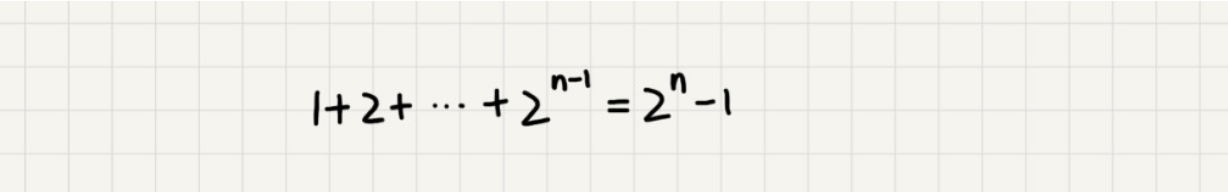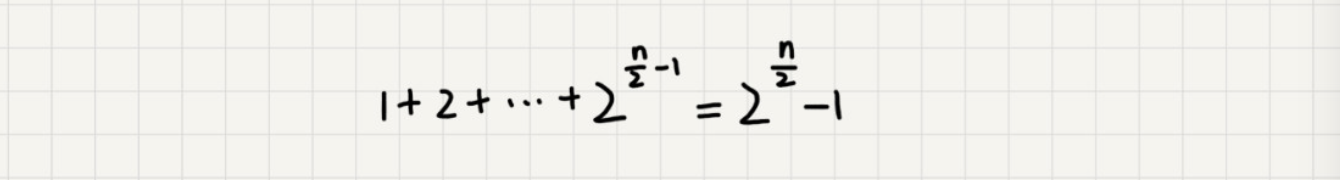数据结构与算法-学习笔记（19）作用：求解递归算法的时间复杂度。把递归的函数调用过程，逐层分解画成图，其实就是一棵树。

作用：求解递归算法的时间复杂度。

把递归的函数调用过程，逐层分解画成图，其实就是一棵树。

如下是根据斐波那契数列的递推公式画的图：

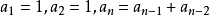
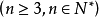
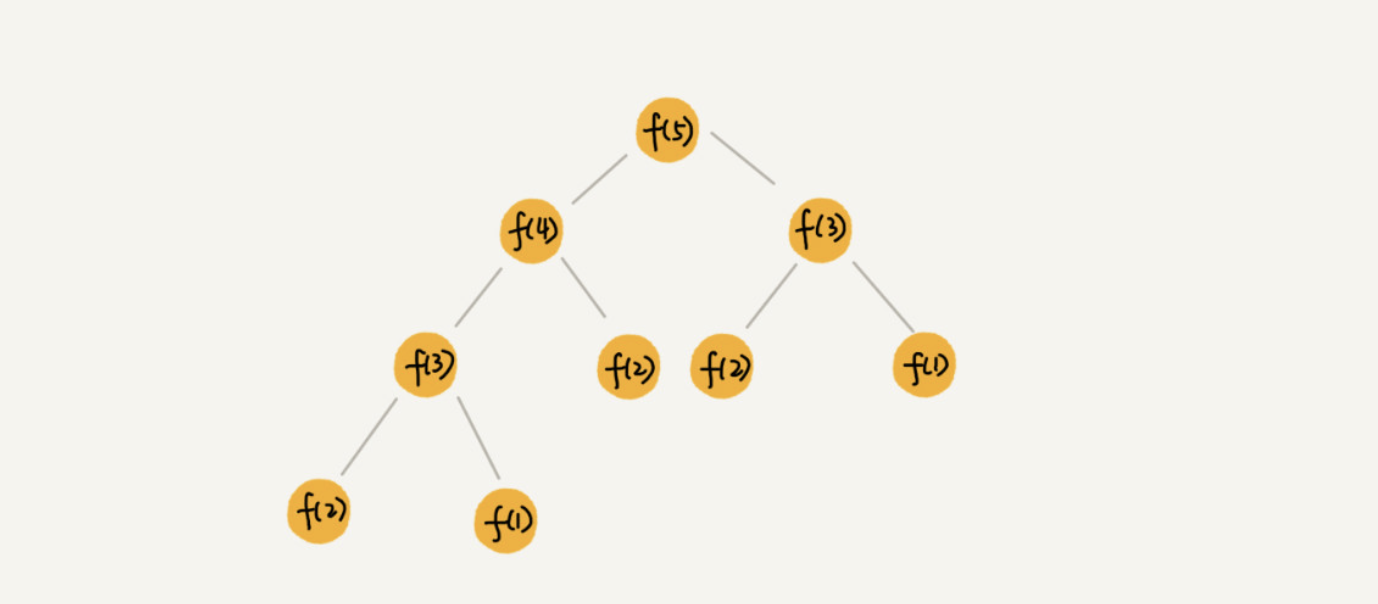
如何用递归树求解时间复杂度呢？

总时间=所有层数消耗时间的和；

如果每层消耗时间相同，那么O(n*h)。

如果每层消耗时间不同，那么O(h1+h2+...)

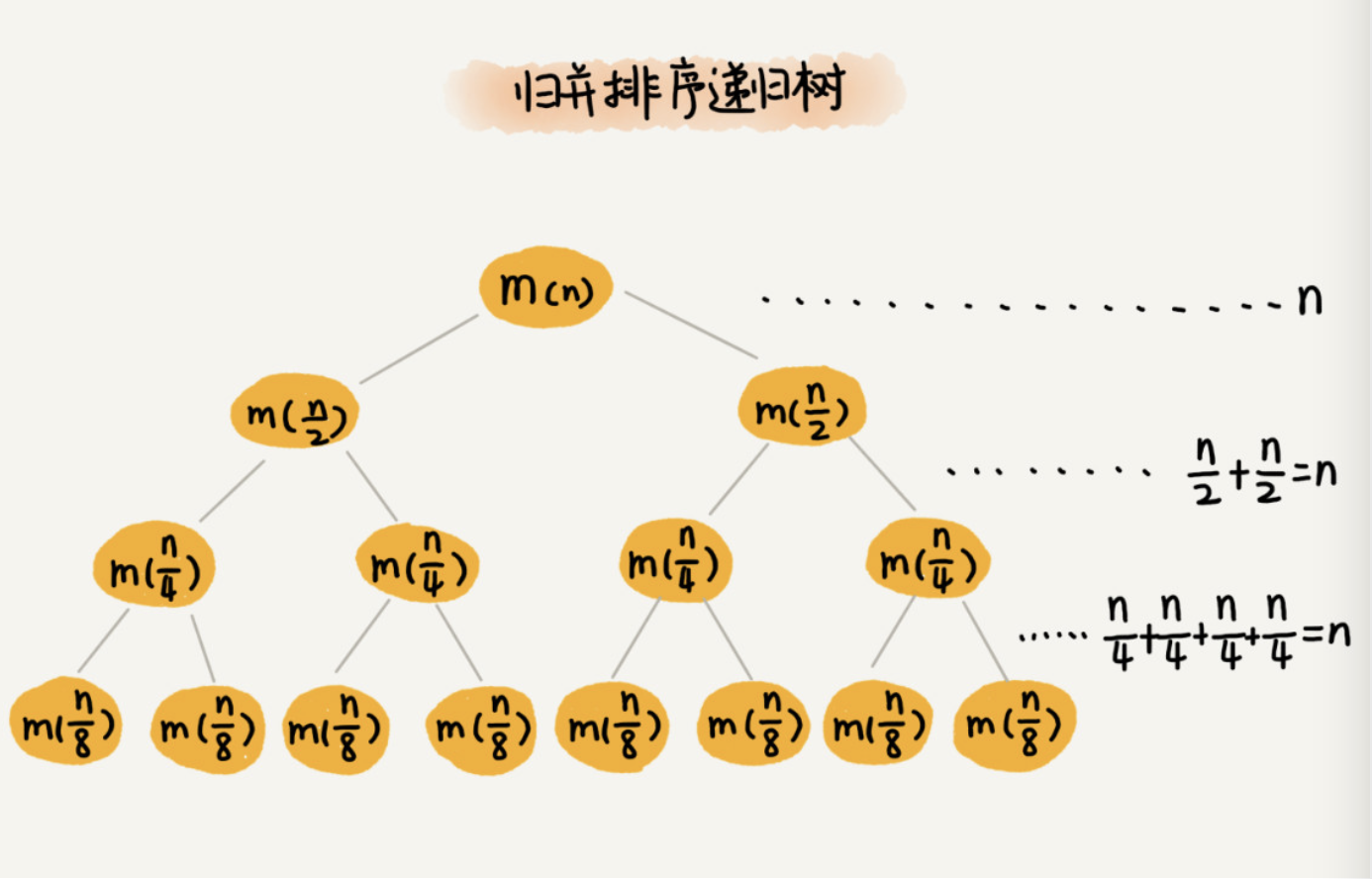
归并排序主要有两步：1.将数据一分为二 2.合并。分解的时间就是常量了。合并：把两个数组合并，时间和数据规模n有关，可以记作n。因此每一层的时间消耗是n，满二叉树层数log2n。总的时间复杂度O(n*h) = O(nlogn)

练习：

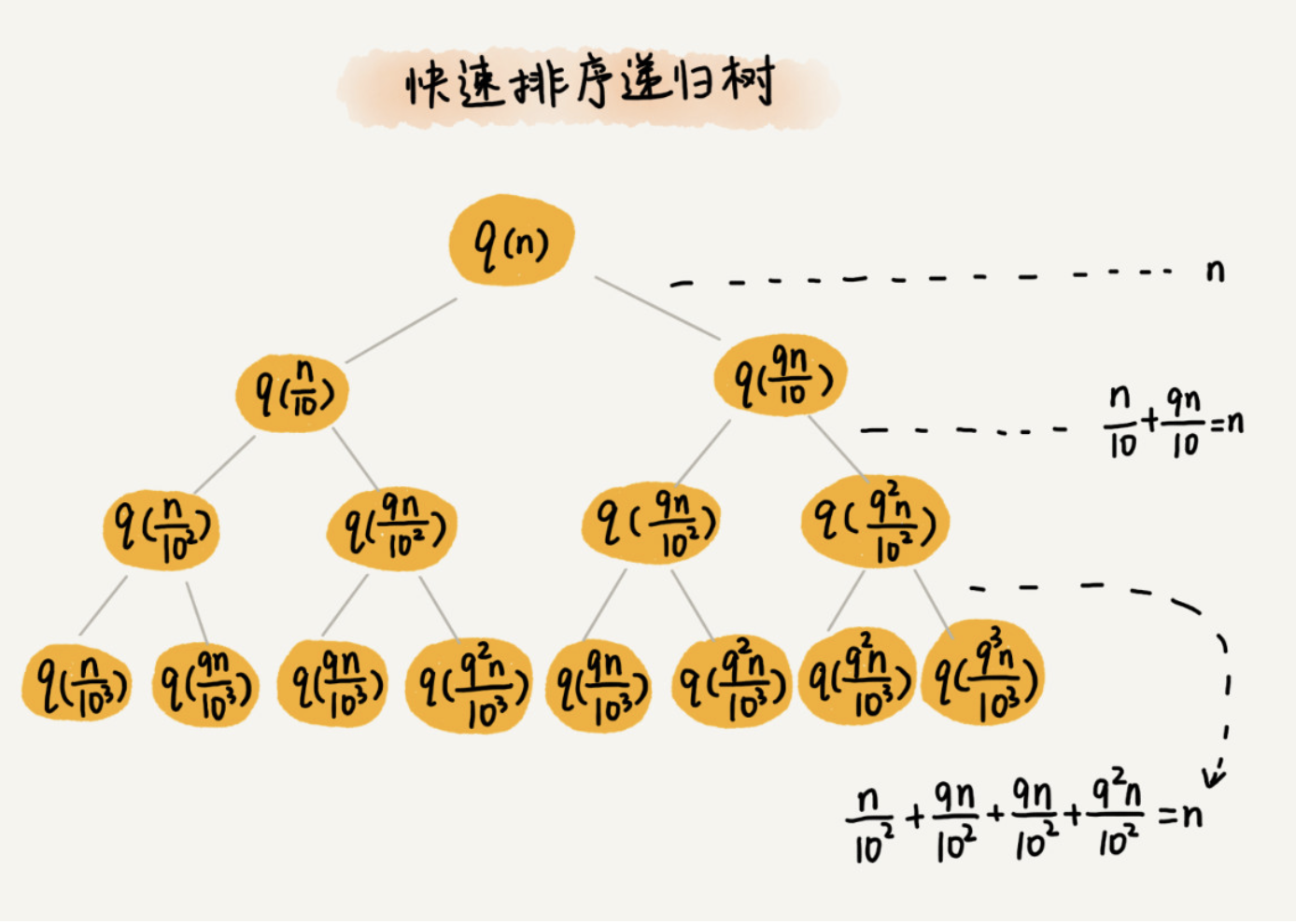
每一层的操作就是：求分区点位置，分区。求分区点位置时间n，总的n。O(nh)。

那么现在求树高h也就是有多少层。

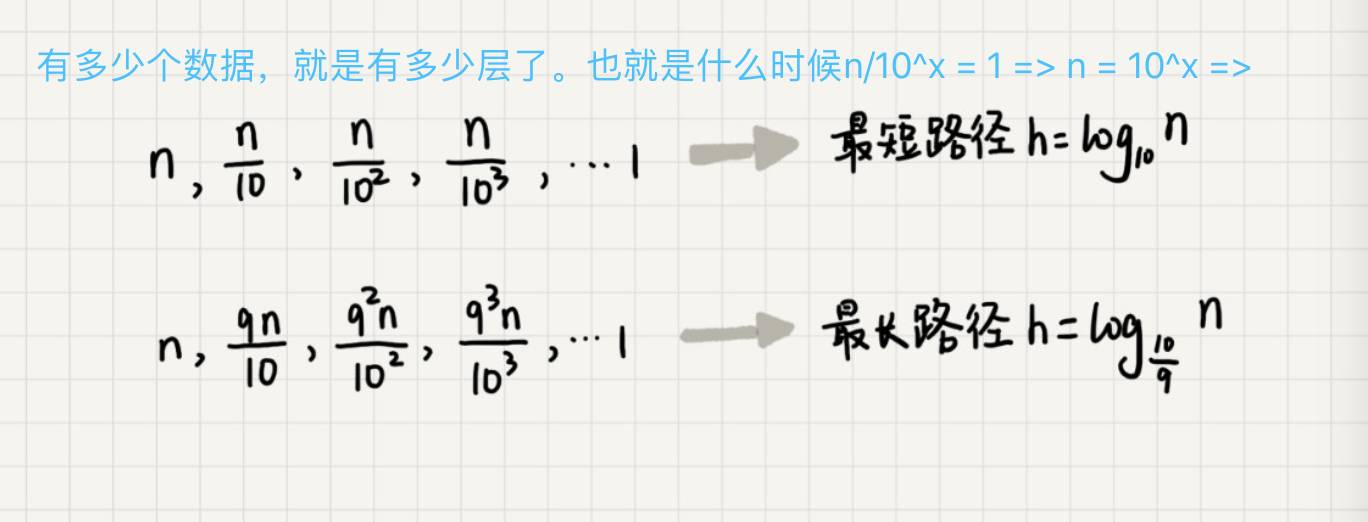
O(nlogn)

F(1)=1，F(2)=1, F(n)=F(n-1)+F(n-2)（n>=3，n∈N*）

层数：

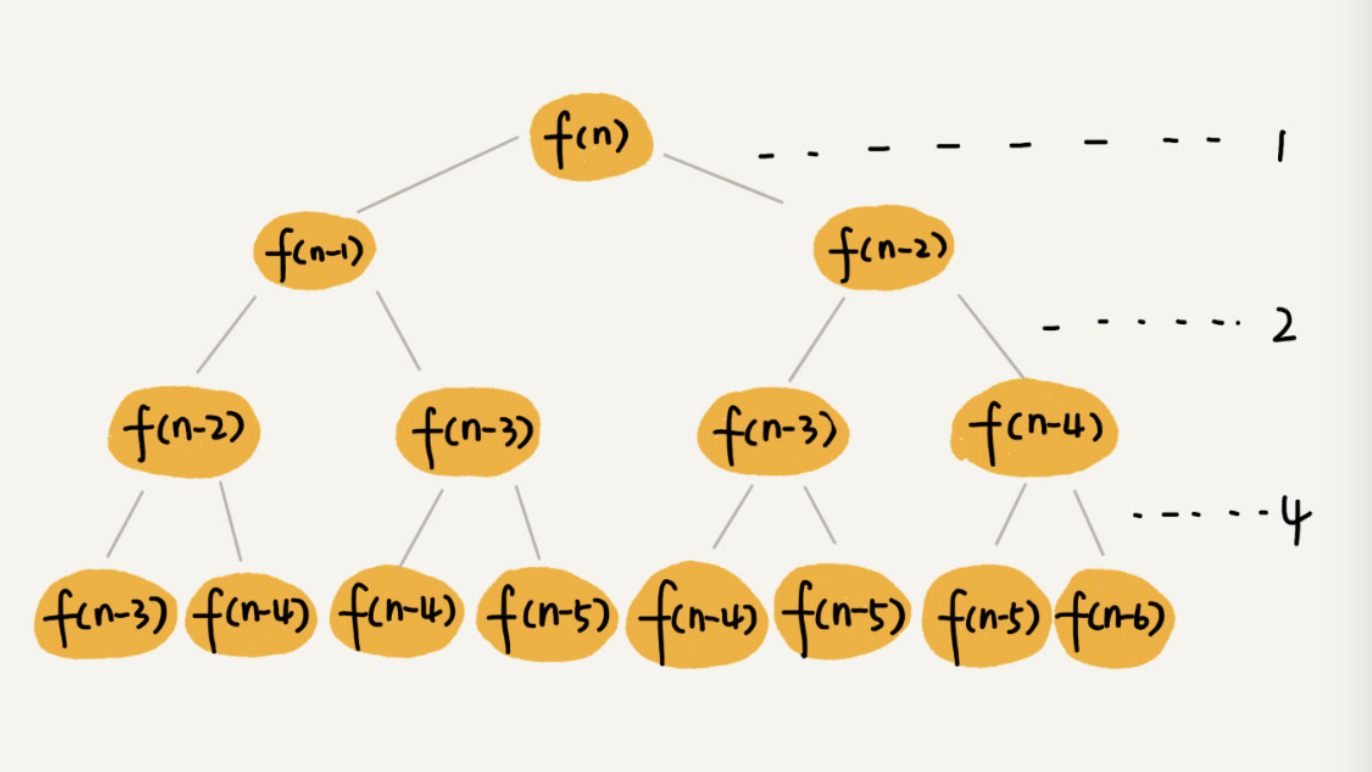
最短路径n、n-2、n-4....1 =n/2 最长路径n、n-1、n-2....1 =n

每层时间：每组加和时间的总和，加和时间1，组数=2^(h-1)。每层总时间是2^(h-1)。

如果路径长度n：

如果路径长度n/2:

指数级的时间复杂度了。