树
没有父节点的节点叫做根节点。没有子节点的节点叫做叶子节点或叶节点。
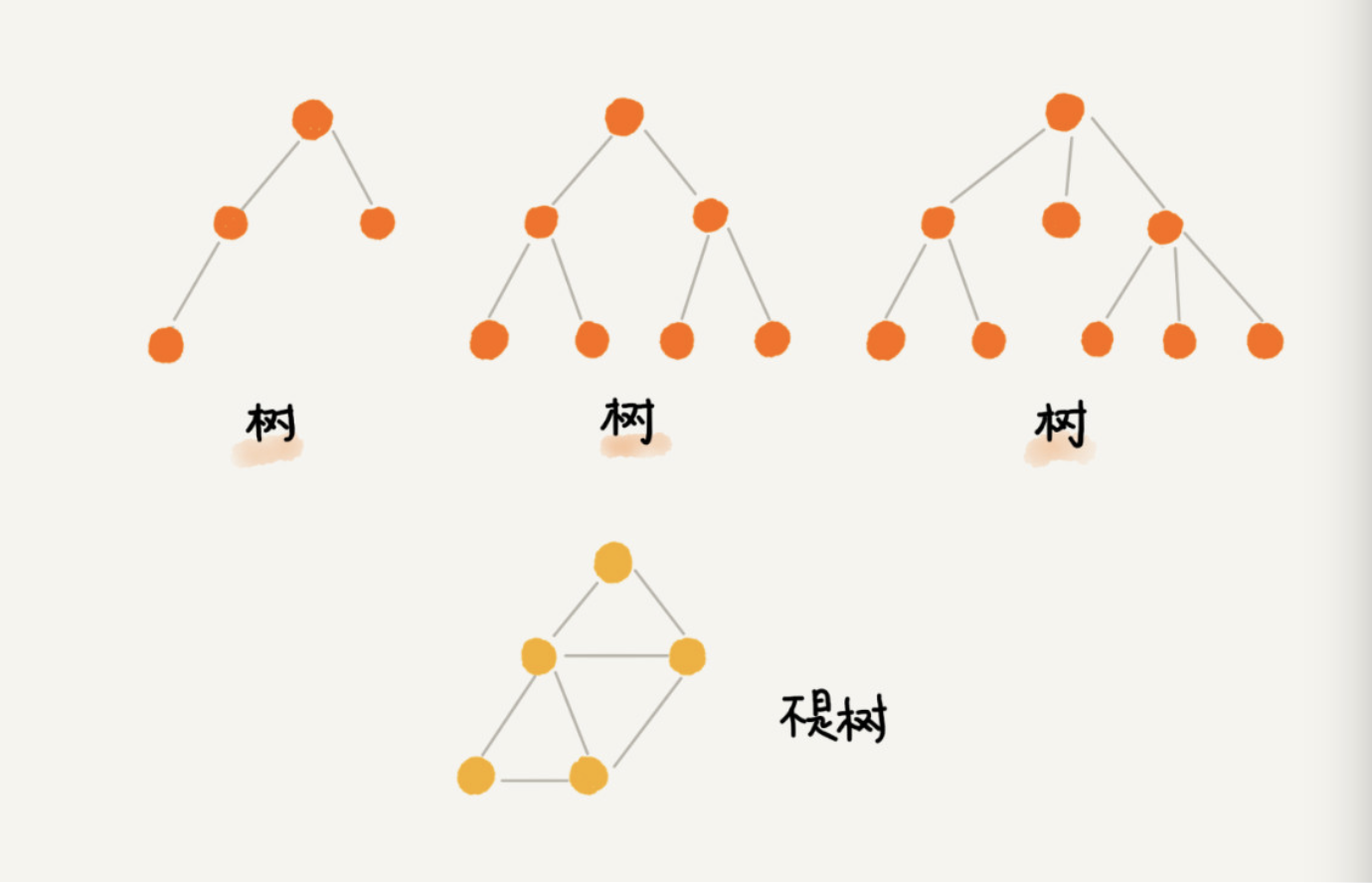
关于树还有三个相似概念:高度(Height)、深度(Depth)、层(Level)。

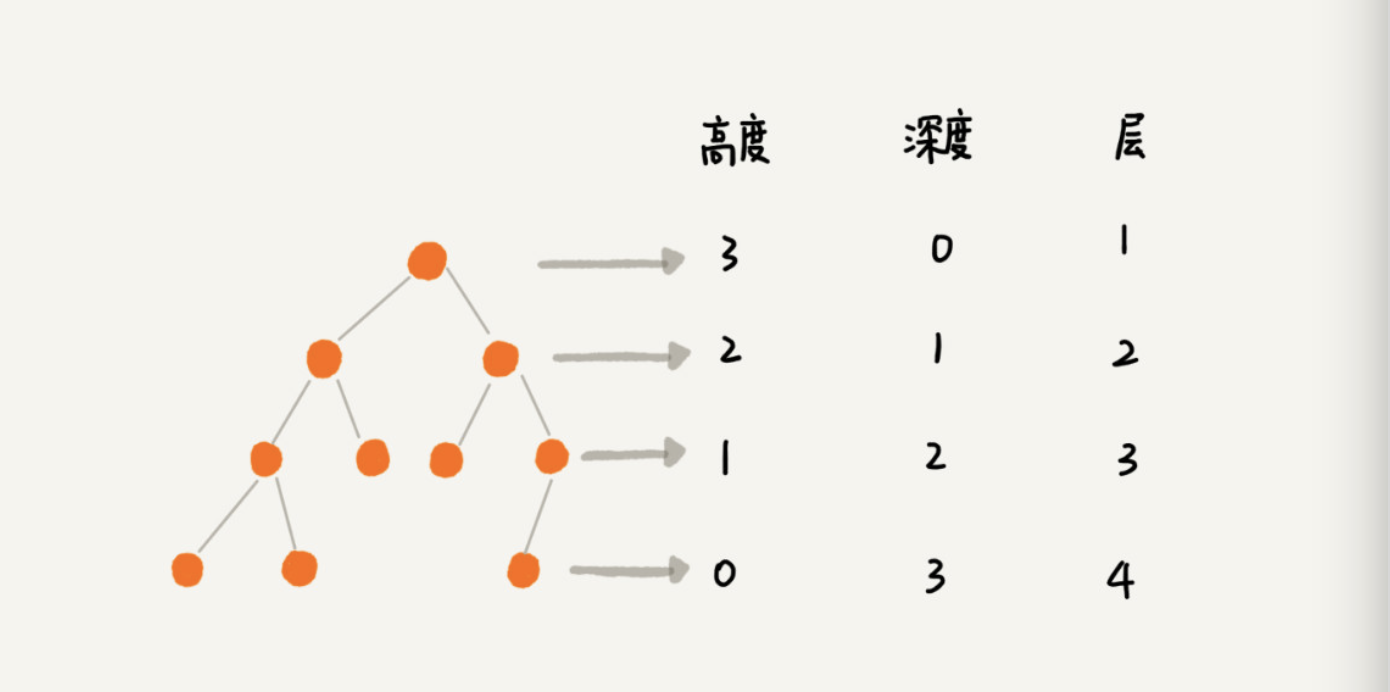
二叉树
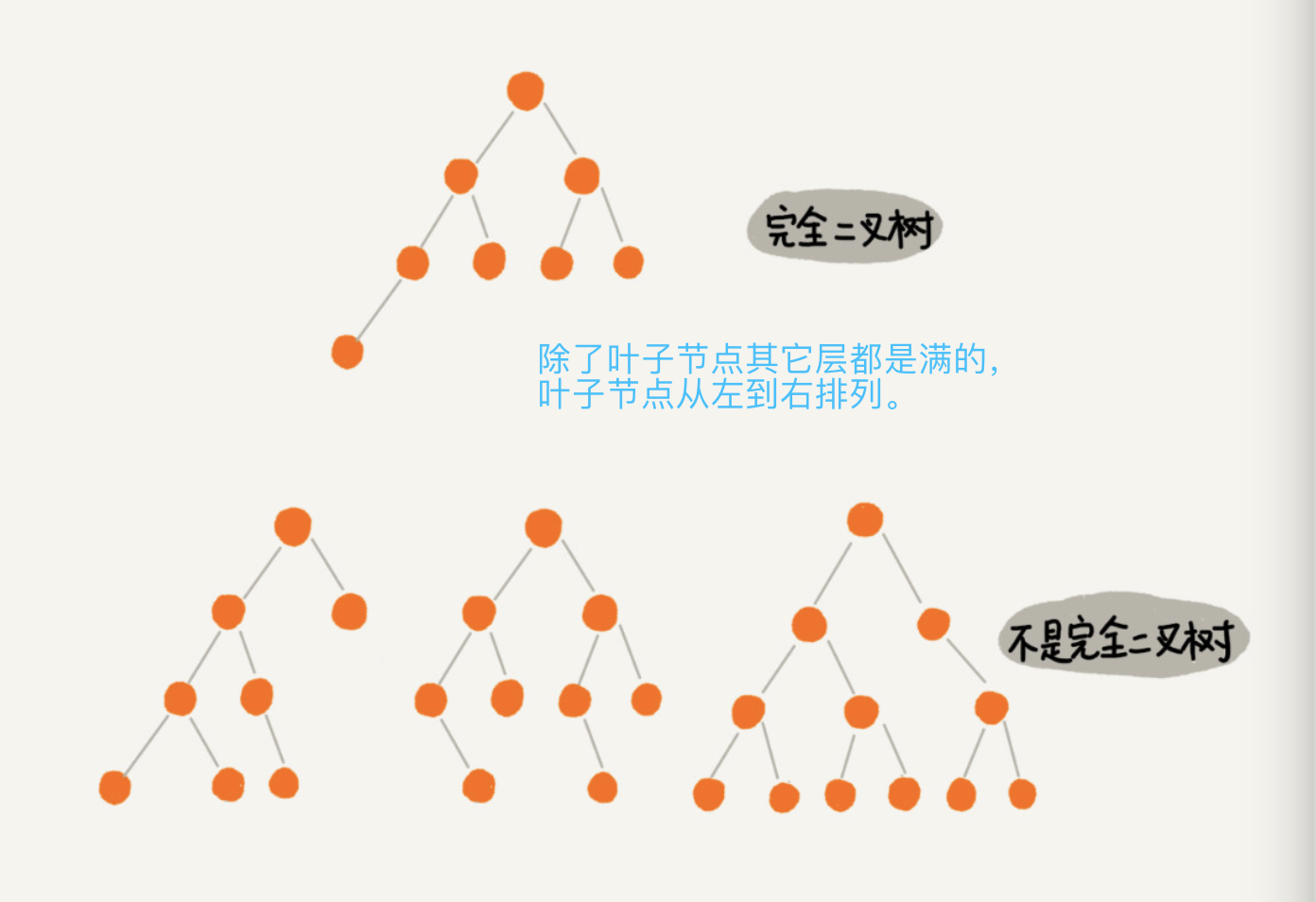
如何表示或者存储一颗二叉树
- 基于指针的二叉链式存储
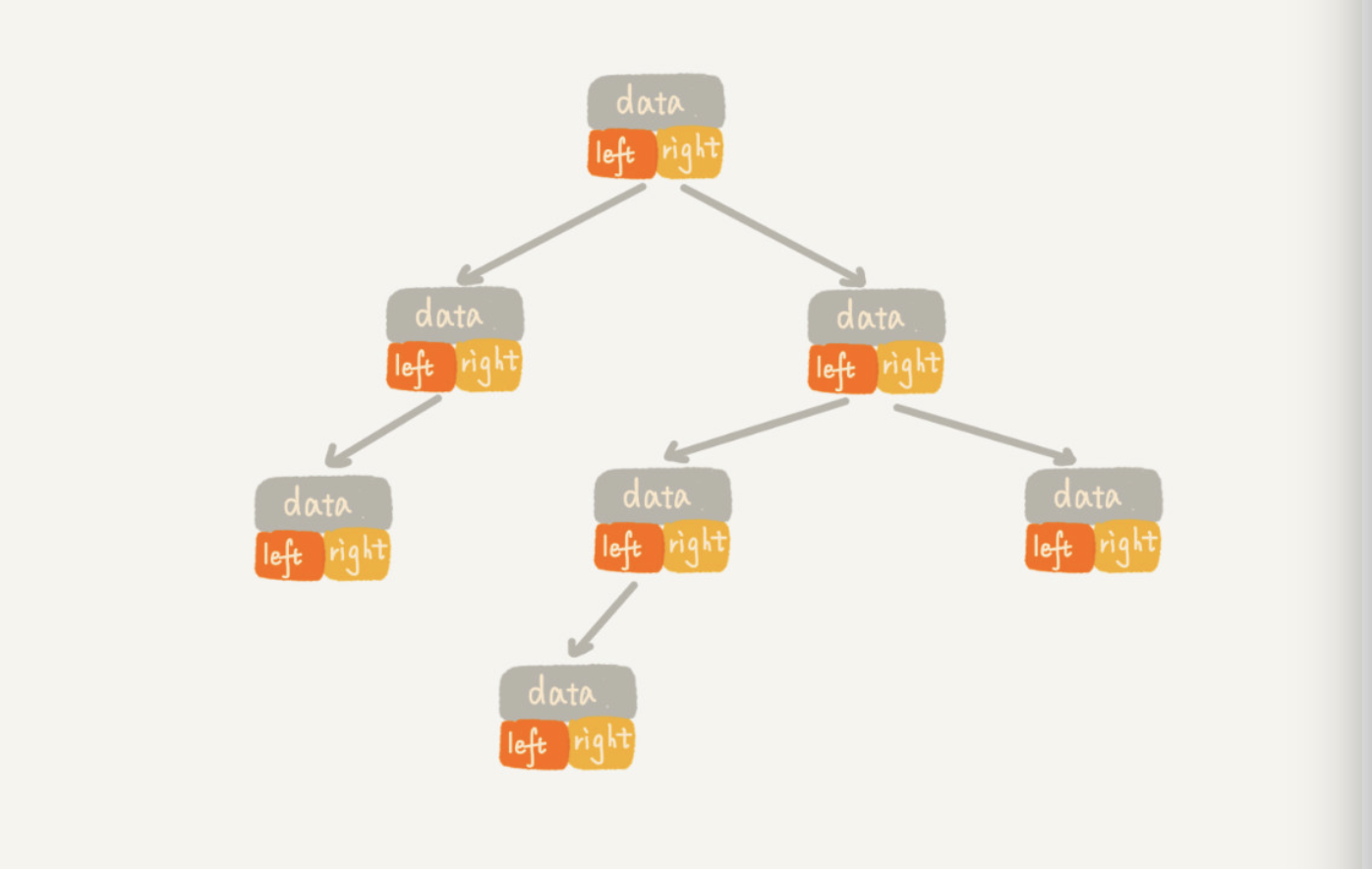
- 基于数组的顺序存储:更适合完全二叉树(浪费最少空间)
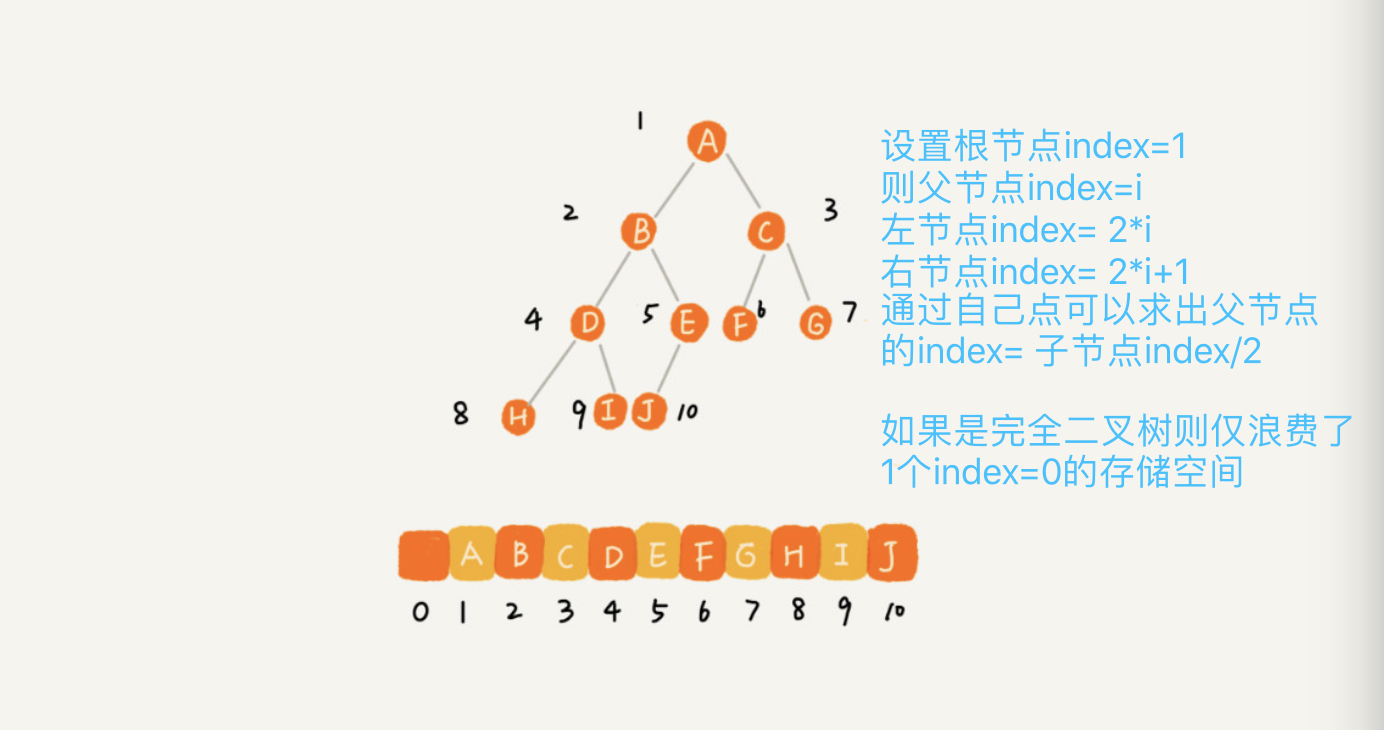
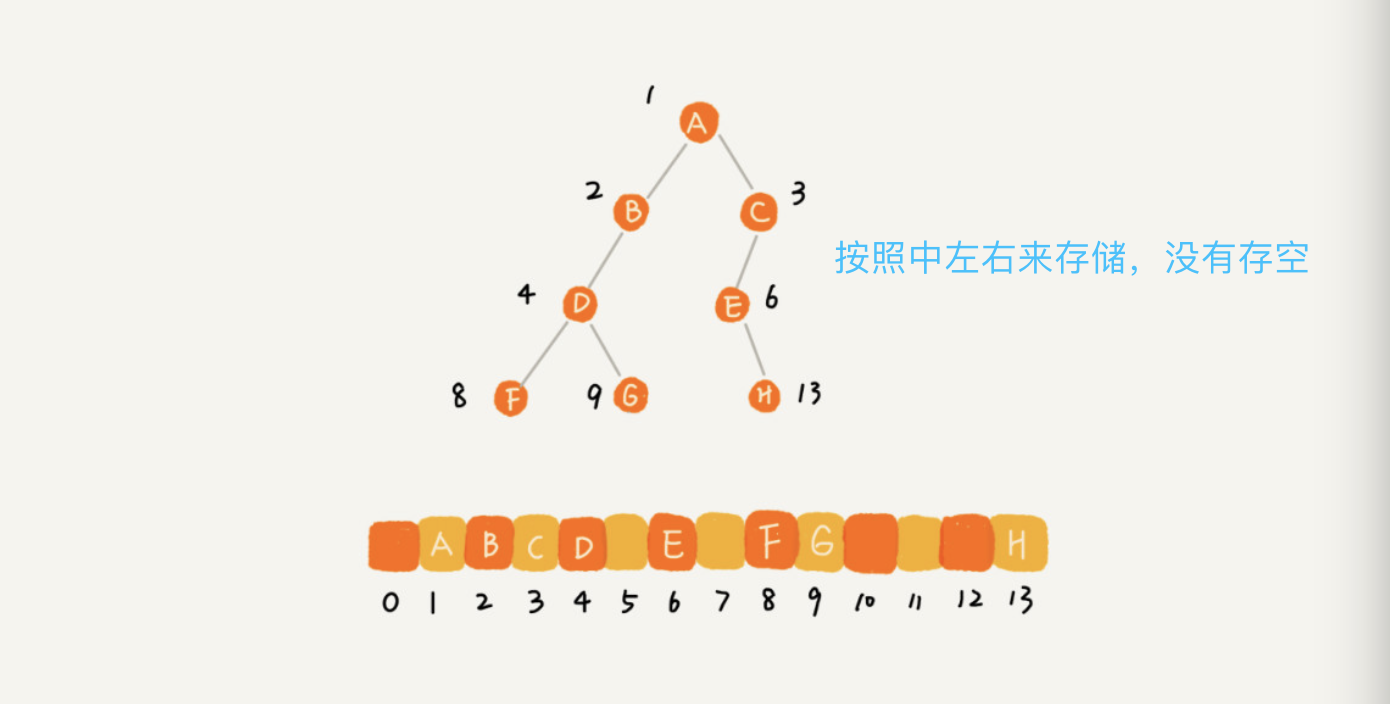
二叉树的遍历
三种方法:前序遍历、中序遍历、后序遍历(前中后指的是根节点的位置)。遍历是一个递归的过程。
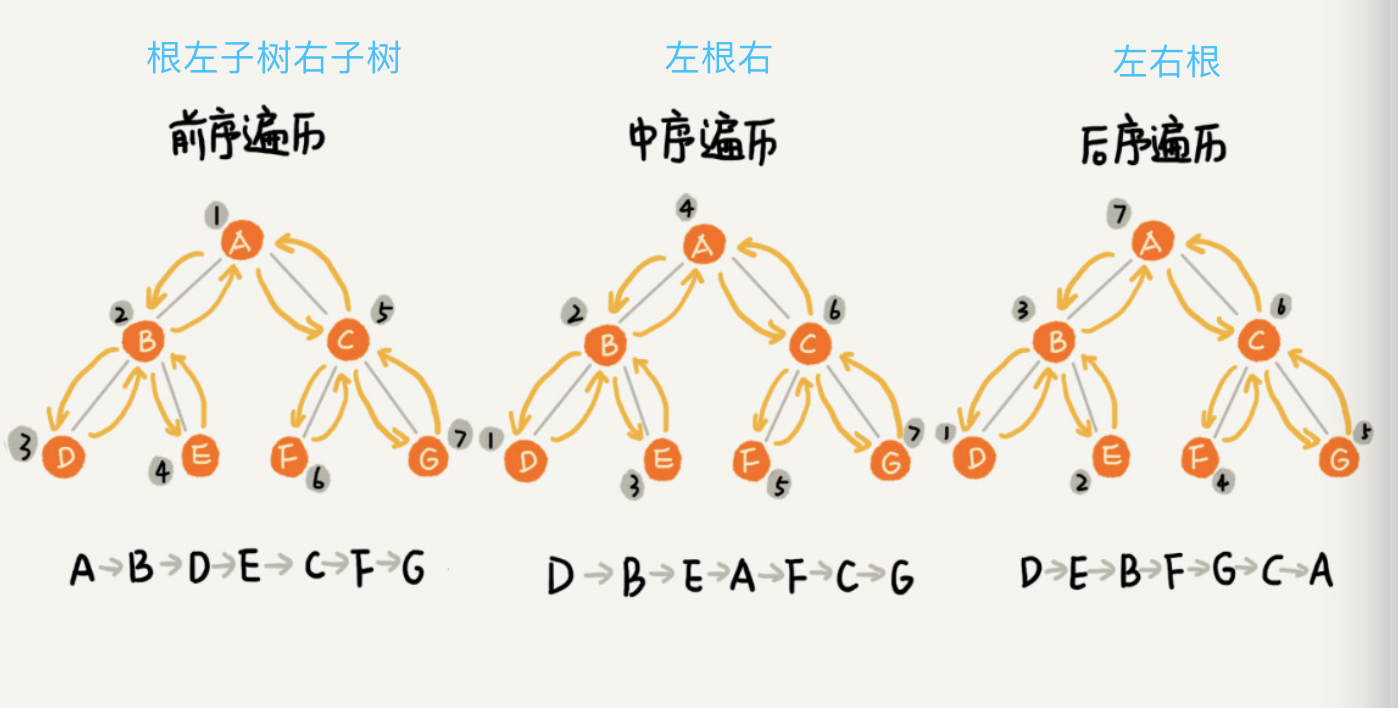
递归公式:
前序遍历的递推公式:
preOrder(r) = print r->preOrder(r->left)->preOrder(r->right)
中序遍历的递推公式:
inOrder(r) = inOrder(r->left)->print r->inOrder(r->right)
后序遍历的递推公式:
postOrder(r) = postOrder(r->left)->postOrder(r->right)->print r
// 出口就是r=nil
typedef struct TreeNode {
int data;
struct TreeNode *left;
struct TreeNode *right;
} Node;
void preOrder(Node *root) {
if (!root) return;
printf("%d",root->data);
preOrder(root->left);
preOrder(root->right);
}
void inOrder(Node *root) {
if (!root) return;
inOrder(root->left);
printf("%d", root->data);
inOrder(root->right);
}
void postOrder(Node *root) {
if (!root) return;
postOrder(root->left);
postOrder(root->right);
printf("%d",root->data);
}
遍历的时间复杂度:每个节点最多被访问两次,所以遍历的时间复杂度跟节点个数n成正比,因此O(n);
思考题
Q: 给定一组数据,可以构建出多少种不同的二叉树?
A:完全二叉树可以存储为一个数组,则树的排序也就是数组中n个数据的排序:n!
二叉查找树
二叉查找树支持快速查找、插入、删除数据。
二叉查找树的要求:在树中的任意一个节点,其左子树中的每个节点值,都要小于这个节点的值,而右子树中节点值都大于这个节点的值。因此不能有重复的数据。(左子树<父节点<右节点)
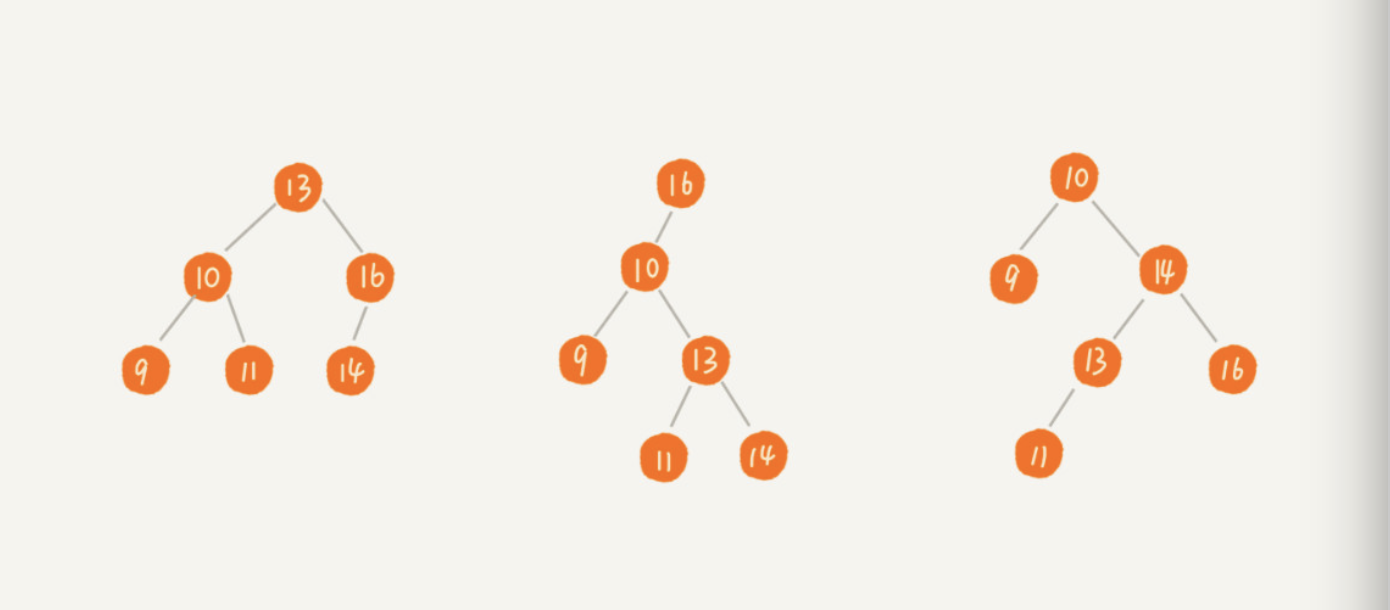
查找
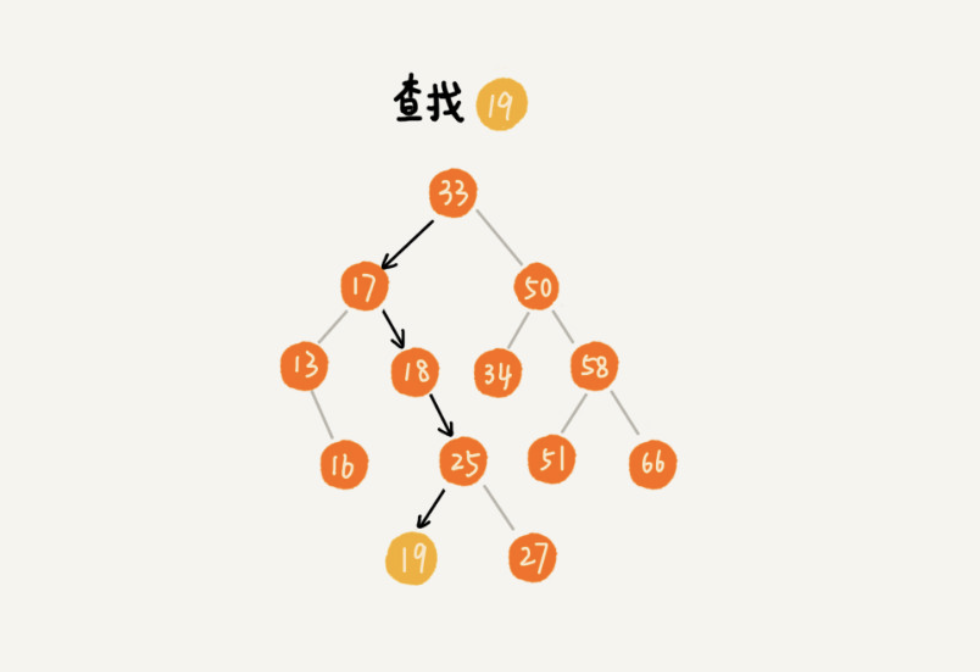
Node* search(Node *root, int data) {
if (!root) return nil;
if (data == root->data) {
return root;
} else if (data > root->data) {
return search(root->right, data);
} else {
return search(root->left, data);
}
}
Node * search2(Node *root, int data) {
while (root != nil) {
if (data == root->data) {
return root;
} else if (data > root->data) {
root = root->right;
} else {
root = root->left;
}
}
return nil;
}
插入
类似查找。把新插入的数据放在叶子节点上,这样既不影响二叉查找树的特性,又不需要破坏原本树的结构。
void insert(Node *root, int data) {
if (!root) {
// 注意结构体指针的赋值 Node *node = {data, nil, nil}不行的,此时node是个指针,却把结构体值类型数据赋值给它了(int *a = 2❎)
/* 平时
① NSObject *obj = [[NSObject alloc] init];
obj 它也是一个指向NSObject类型对象数据的指针,[[NSObject alloc] init]返回的也是一个指针,而不是实际的对象的值
② char *b = "String"; "String"字符串常量,它返回给b的也是地址。
③ obj = nil;让obj指针变量置空,也就是让它指向空,nil是空指针的意思,不是让obj所指向的数据置空
*/
Node node = {data, nil, nil};
root = &node;
}
while (root != nil) {
if (data > root->data) {
if (!root->right) {
Node node = {data, nil, nil};
root->right = &node;
return;
} else {
root = root->right;
}
} else {
if (!root->left) {
Node node = {data, nil, nil};
root->left = &node;
return;
} else {
root = root->left;
}
}
}
}
删除
分三种情况:
- 要删除的节点没有子节点,即叶子节点;
- 要删除的节点只有一个子节点;
- 要删除的节点有两个子节点。
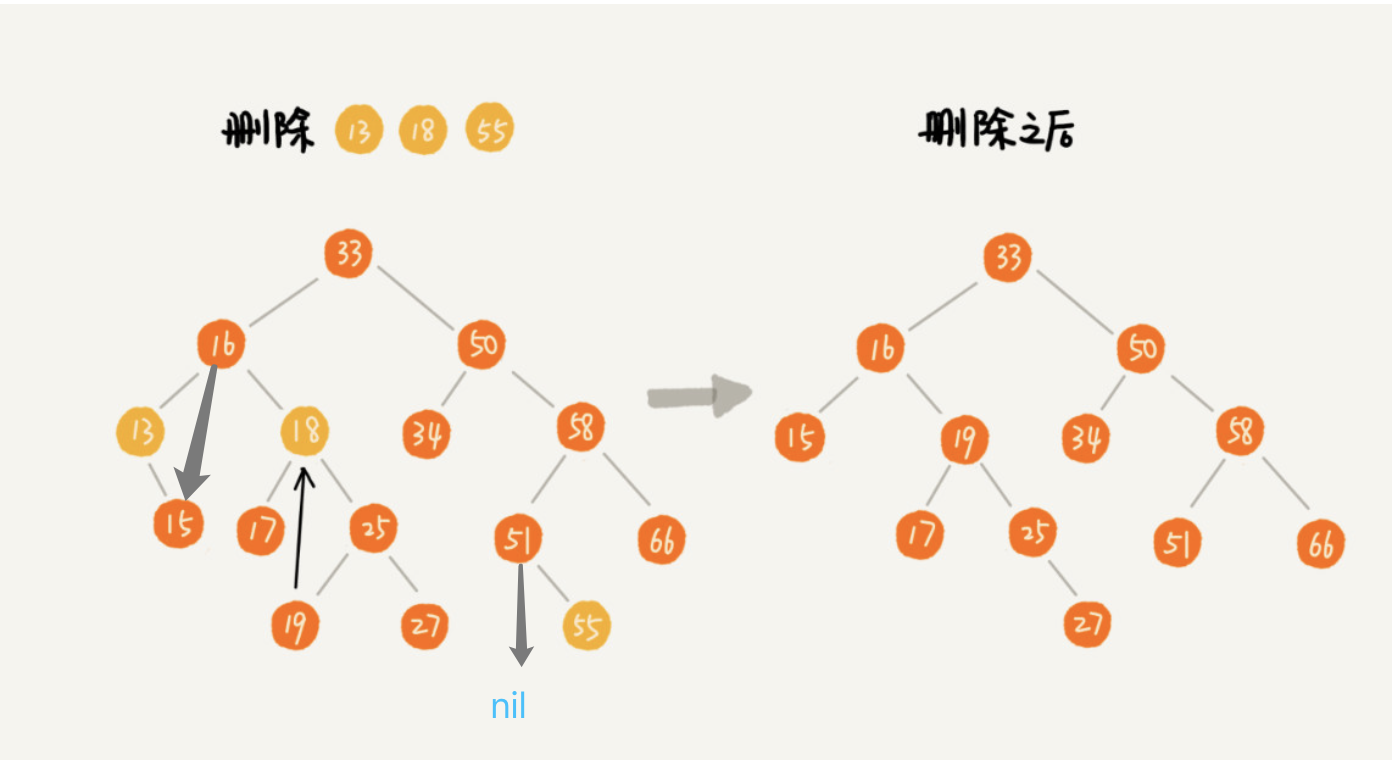
int delete(Node *root, int data) {
if (!root) return -1;
Node *preNode = nil;
BOOL find = NO;
while (root != nil) {
if (root->data == data) {
find = YES;
break;
}
preNode = root;
if (root->data > data) {
root = root->left;
} else {
root = root->right;
}
}
if (!find) return -1;
if (!root->left && !root->right) {
if (preNode->left == root) preNode->left = nil;
else preNode->right = nil;
return 1;
}
if (!root->left || !root->right) {
Node *child = nil;
if (!root->left) {
child = root->right;
} else {
child = root->left;
}
if (preNode->left == root) preNode->left = child;
else preNode->right = child;
return 1;
}
Node *min = root->right;
Node *preM = root;
while (!min) {
preM = min;
min = min->left;
}
root->data = min->data;
if (preM != root) {
if (min->right) preM->left = min->right;
else preM->left = nil;
} else {
preM->right = nil;
}
return 1;
}
其他操作
可以快速排序:
中序遍历二叉查找树,可以输出有序数据列,O(n)。
支持重复数据的二叉查找树
实际开发中每个节点的数据可以是一个更大的结构,如包含很多字段的对象,我们利用某个字段作为key来构建树。
这样如果存在相同键值的对象,怎么解决:
- 每个节点不止可以存储一个数据,可以存储链表、数组等结构,key相同的数据都存储在同一节点。
typedef struct TreeNode {
int key;
struct TreeNode *left;
struct TreeNode *right;
NSMutableArray *data;
} Node;
- 每个节点仍存储一个数据,遇到相同节点,就当做大于当前节点,继续向右走直到走到叶子节点,插入。(同理当做小于,向左走也可以)这样查询和删除就需要一直向下走直到走到叶子节点,把所有相同的找出、删除。
时间复杂度
相同一组数据二叉查找树的排列方式会有很多种:

对于极度不平衡的树,他们已经接近链表了,查找插入删除O(n)。
对于完全二叉树,时间复杂度和树的层数L成正比。除了底层,每层包含的节点数2^(L-1)。
// 假设最大层数为K
n >= 1+2+4+8+...+2^(K-2)+1
n <= 1+2+4+8+...+2^(K-2)+2^(K-1)
借助等比数列求和公式,算出K的范围[log2(n+1), log2n+1],也就得出时间复杂度O(logn)
注:等比数列(每一项与它前一项的比都是同一个常数,也叫公比 q)
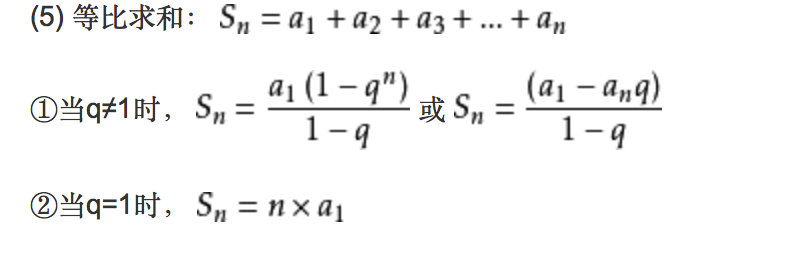
思考题
求树的高度?
用递归的思想:height = Max(Height(left), Height(right))+1;