很多地方的推导太长了。
首先: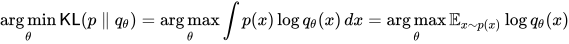
写成 MLE,比 KL 散度少一个常数,形式更简单。没必要时刻写出 KL 散度。
可以 1 步推导出 VAE。
这个是 MLE:
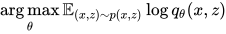
显然等价于:
![\mathop{\arg\max}_\theta \mathbb{E}_{x \sim p(x)} \Big[ \mathbb{E}_{z \sim p(z|x)} \Big[ \log q_\theta(x|z) + \log q_\theta(z) \Big] \Big]](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/12/5/1677ca76a2da54c2~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png)
恭喜,推导出了 VAE。
加 10 秒钟,把它变成更常见的样子。
展开:
![\mathop{\arg\max}_\theta \mathbb{E}_{x \sim p(x)} \Big[ \mathbb{E}_{z \sim p(z|x)} \log q_\theta(x|z) + \mathbb{E}_{z \sim p(z|x)} \log q_\theta(z) \Big]](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/12/5/1677ca7693e62289~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png)
改变符号,显然等价于:
![\mathop{\arg\min}_\theta \mathbb{E}_{x \sim p(x)} \Big[ \mathbb{E}_{z \sim p(z|x)} - \log q_\theta(x|z) + \mathsf{KL}\big( p(z|x) \parallel \log q_\theta(z)\big) \Big]](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/12/5/1677ca76a104e8a7~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png)
再加上先验:
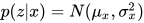
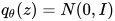
还有假设 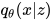 是固定 stdev 的 Gaussian 以造出 MSE。
是固定 stdev 的 Gaussian 以造出 MSE。
就和实际用的一模一样了。
我在另一篇文章,简单实验了 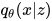 有可变 stdev 的情况:
有可变 stdev 的情况:

很多地方的推导太长了。
首先: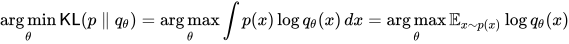
写成 MLE,比 KL 散度少一个常数,形式更简单。没必要时刻写出 KL 散度。
可以 1 步推导出 VAE。
这个是 MLE:
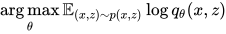
显然等价于:
![\mathop{\arg\max}_\theta \mathbb{E}_{x \sim p(x)} \Big[ \mathbb{E}_{z \sim p(z|x)} \Big[ \log q_\theta(x|z) + \log q_\theta(z) \Big] \Big]](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/12/5/1677ca76a2da54c2~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png)
恭喜,推导出了 VAE。
加 10 秒钟,把它变成更常见的样子。
展开:
![\mathop{\arg\max}_\theta \mathbb{E}_{x \sim p(x)} \Big[ \mathbb{E}_{z \sim p(z|x)} \log q_\theta(x|z) + \mathbb{E}_{z \sim p(z|x)} \log q_\theta(z) \Big]](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/12/5/1677ca7693e62289~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png)
改变符号,显然等价于:
![\mathop{\arg\min}_\theta \mathbb{E}_{x \sim p(x)} \Big[ \mathbb{E}_{z \sim p(z|x)} - \log q_\theta(x|z) + \mathsf{KL}\big( p(z|x) \parallel \log q_\theta(z)\big) \Big]](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/12/5/1677ca76a104e8a7~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png)
再加上先验:
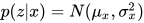
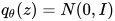
还有假设 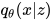 是固定 stdev 的 Gaussian 以造出 MSE。
是固定 stdev 的 Gaussian 以造出 MSE。
就和实际用的一模一样了。
我在另一篇文章,简单实验了 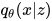 有可变 stdev 的情况:
有可变 stdev 的情况:
