在上一节里介绍了简单带类型的λ-calculus的定义和基本性质, 这一节将介绍引入类型对λ-calculus系统的影响, 最重要的即是类型保证了系统的强正规性(strong normalization), 另外还将介绍类型检查与类型重建的方法(这一部分也是函数式编程应用里比较多关注的内容).
弱正规化定理(Weak normalization theorem)
定义: 类型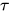 的度(degree)记作
的度(degree)记作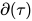 , 定义如下:
, 定义如下: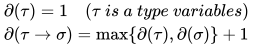
定义: 可约式(redex)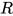 的度(degree)记作
的度(degree)记作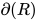 , 定义如下:
, 定义如下:
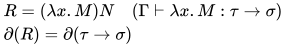
定义: 表达式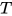 的度(degree)记作
的度(degree)记作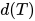 , 定义为其所包含的所有可约式(redex)的度的最大值. 若
, 定义为其所包含的所有可约式(redex)的度的最大值. 若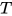 为normal form, 则
为normal form, 则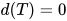 .
.
引理1: ![d(T[U/x])\leq \max\{d(T),d(U),\partial(\tau)\}](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7e7e04d990~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) , 其中
, 其中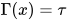 (即
(即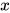 的类型为
的类型为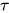 ).
).
证明: 对于![T[U/x]](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7eb1ed16b9~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) 中的所有可约式
中的所有可约式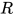 有以下几种情况
有以下几种情况
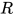 是
是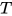 中原有的可约式.
中原有的可约式. 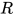 在替换中不变, 显然有
在替换中不变, 显然有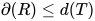 .
.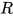 是
是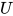 中的可约式.
中的可约式. 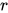 在替换中引入, 显然有
在替换中引入, 显然有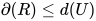 .
.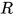 是在替换
是在替换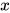 后所产生的新可约式, 根据
后所产生的新可约式, 根据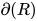 定义有
定义有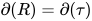 .
.
那么对于可约式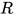 有
有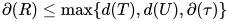 , 故根据表达式度的定义有
, 故根据表达式度的定义有![d(T[U/x])\leq \max\{d(T),d(U),\partial(\tau)\}](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7e7eb9dc7d~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) .
.
证毕.
引理2: 若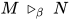 那么
那么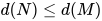 .
.
证明: 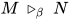 即
即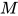 中的某个可约式形如
中的某个可约式形如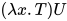 规约为
规约为![T[U/x]](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7e7ee79151~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) , 对于
, 对于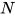 中的所有可约式
中的所有可约式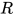 有以下几种情况
有以下几种情况
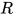 属于
属于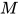 在规约中不变, 显然
在规约中不变, 显然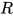 的度不发生改变,
的度不发生改变, 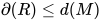 .
.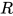 来自于
来自于![T[U/x]](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7e7f2c728f~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) 内部, 由引理1给出
内部, 由引理1给出![d(T[U/x])\leq \max\{d(T),d(U),\partial(\tau)\}](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7e7f3c0d4f~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) (
(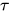 为
为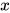 的类型), 其中
的类型), 其中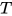 与
与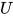 包含在
包含在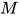 内, 那么有
内, 那么有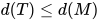 ,
, 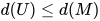 . 并且根据定义有:
. 并且根据定义有: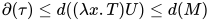 (
(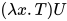 为
为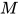 中的一个可约式). 故
中的一个可约式). 故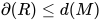 .
.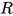 来自于将
来自于将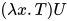 规约为
规约为![T[U/x]](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7e7fbda7bd~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) 后所产生的新可约式, 根据
后所产生的新可约式, 根据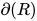 的定义有
的定义有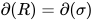 其中
其中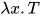 的类型为
的类型为 ,
, 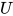 的类型为
的类型为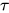 . 又有
. 又有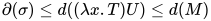 , 故
, 故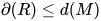 .
.
那么对于可约式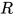 有
有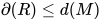 , 故根据表达式度的定义有
, 故根据表达式度的定义有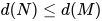 .
.
证毕.
引理3: 若对于一个可约式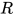 , 其内部包含的所有的可约式的度均小于
, 其内部包含的所有的可约式的度均小于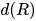 , 对
, 对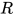 进行规约后得到的表达式
进行规约后得到的表达式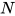 有
有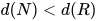 .
.
证明: 可约式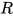 形如
形如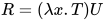 且
且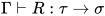 , 那么
, 那么![N=T[U/x]](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7e87911b4e~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) , 其中
, 其中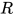 内部包含的所有的可约式的度均小于
内部包含的所有的可约式的度均小于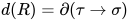 , 即有
, 即有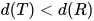 与
与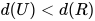 . 根据引理1有
. 根据引理1有![d(T[U/x])\leq \max\{d(T),d(U),\partial(\tau)\}<d(R)](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7e87b55dc6~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) 即
即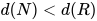 .
.
证毕.
定理1: 弱正规化定理(weak normalization theorem)
简单带类型的λ-calculus具有弱规范性(weak normalization). 即所有简单带类型的λ-calculus表达式均是弱规范化的, 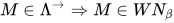 .
.
证明:
对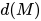 做归纳.
做归纳.
归纳基础: 当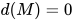 时,
时, 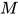 为normal form, 显然
为normal form, 显然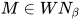 .
.
归纳步骤: 归纳假设当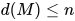 时均有
时均有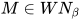 .
.
当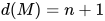 时, 选取
时, 选取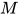 中
中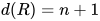 的可约式
的可约式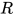 , 且
, 且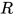 内部包含的所有的可约式的度均小于
内部包含的所有的可约式的度均小于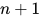 (即满足度为
(即满足度为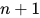 最右可约式). 由引理3得, 对
最右可约式). 由引理3得, 对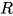 进行规约后
进行规约后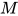 中度为
中度为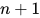 的可约式将会减少. 重复该操作直至规约至
的可约式将会减少. 重复该操作直至规约至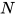 , 其中
, 其中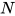 中不存在
中不存在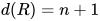 的可约式
的可约式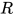 , 此时
, 此时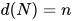 . 由归纳假设得
. 由归纳假设得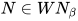 , 且有
, 且有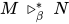 , 即
, 即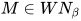 .
.
故由归纳法得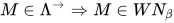 .
.
证毕.
由简单带类型λ-calculus具有弱规范性, 通过leftmost reduction可得到表达式的normal form(参见第四节定理leftmost reduction).
强正规化定理(Strong normalization theorem)
这里介绍简单带类型λ-calculus强正规性的两种证明, 第一种证明方式将带类型λ-calculus转化为带类型λI-calculus形式, 利用λI-calculus系统中弱规范性等价于强规范性的性质进行证明, 第二种证明方式由W.W. Tait在1967年提出, 主要是利用类型在表达式和正规化子集间建立逻辑关系(logical relation).
第一种证明较为初等, 第二种证明可以简单地拓展到Lambda cube(后文将会介绍)上证明其强规范性.
Proof by λI-calculus
定义: 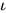 为简单带类型λ-calculus至简单带类型λI-calculus映射
为简单带类型λ-calculus至简单带类型λI-calculus映射
(λI-calculus的定义参见第四节)
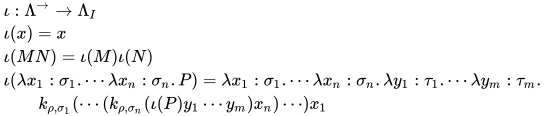
其中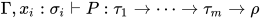 ,
, 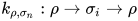 .
.
注: λI-calculus为λ-calculus子集, 简单带类型λI-calculus性质与简单带类型λ-calculus相同.
定义: 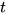 为简单带类型λI-calculus至简单带类型λ-calculus映射
为简单带类型λI-calculus至简单带类型λ-calculus映射
![\begin{align}
&t:\Lambda^{I}\to\Lambda_{\to}\\
&t(M)=\iota(M)[\mathbf{K}_{\rho,\sigma}/k_{\rho,\sigma}]
\end{align}](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7e88d963aa~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png)
其中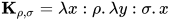 ,
, 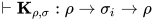 .
.
显然根据定义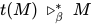 .
.
引理4: 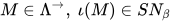 .
.
证明: 由λI-calculus中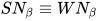 (参见第四节定理(Church, Rosser))及定理1(弱正规化定理)得
(参见第四节定理(Church, Rosser))及定理1(弱正规化定理)得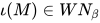 , 故
, 故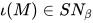 .
.
证毕.
引理5: 对于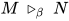 , 其中被规约的可约式形如
, 其中被规约的可约式形如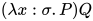 ,
, 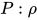 ,
, 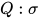 (
(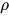 为类型标识符), 则记该类规约为
为类型标识符), 则记该类规约为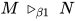 .
.
若有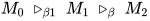 , 则存在
, 则存在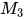 使得
使得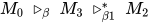 .
.
证明: 在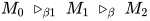 中, 对于
中, 对于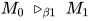 , 进行规约的可约式为
, 进行规约的可约式为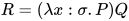 ,
, ![(\lambda x:\sigma.P)Q\;\triangleright_{\beta}\;P[Q/x]](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7e8924b0fa~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) 其中
其中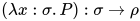 故
故![P[Q/x]:\rho](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7e89dfe03b~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) ,
, ![P[Q/x]](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7e89d59748~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) 的类型
的类型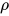 表明
表明![P[Q/x]](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7e8932a1fc~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) 不为抽象(abstraction), 即非
不为抽象(abstraction), 即非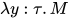 形式. 故
形式. 故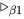 规约后不产生新的可约式. 故
规约后不产生新的可约式. 故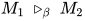 中进行规约的可约式属于
中进行规约的可约式属于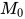 , 可交换规约顺序, 即
, 可交换规约顺序, 即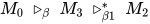 .
.
(在交换规约顺序后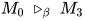 规约中可能会复制出多个可约式
规约中可能会复制出多个可约式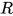 , 故交换后为
, 故交换后为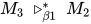 )
)
证毕.
引理6: 若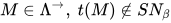 则存在无穷规约序列, 其中所有
则存在无穷规约序列, 其中所有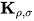 项没被规约.
项没被规约.
证明: 对于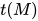 的无穷规约序列,
的无穷规约序列, 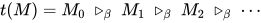 , 若其中出现
, 若其中出现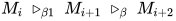 则由引理5得, 可将
则由引理5得, 可将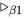 规约交换后置, 即
规约交换后置, 即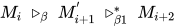 . 则对于任意有限长的前
. 则对于任意有限长的前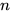 项的子规约序列, 均不存在
项的子规约序列, 均不存在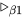 规约, 即存在无穷规约序列不包含
规约, 即存在无穷规约序列不包含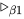 规约.
规约.
在无穷规约序列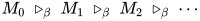 中不存在
中不存在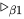 规约, 若其中对
规约, 若其中对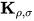 项进行规约
项进行规约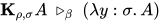 , 其中
, 其中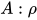 , 由于规约序列中不存在
, 由于规约序列中不存在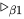 规约, 即
规约, 即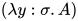 在后续规约没有被规约, 故可对所有
在后续规约没有被规约, 故可对所有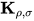 项规约交换后置. 那么有存在无穷规约序列, 对于其任意有限长的前
项规约交换后置. 那么有存在无穷规约序列, 对于其任意有限长的前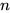 项的子规约序列, 均不存在
项的子规约序列, 均不存在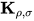 项规约, 即存在无穷规约序列不包含
项规约, 即存在无穷规约序列不包含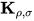 项规约.
项规约.
证毕.
引理7: 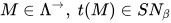 .
.
证明: 若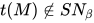 , 由引理5得, 存在无穷规约序列
, 由引理5得, 存在无穷规约序列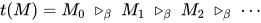 其中所有
其中所有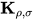 项没有被规约, 那么表达式中的
项没有被规约, 那么表达式中的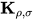 项与标识符
项与标识符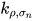 行为无异, 故可构造无穷规约序列
行为无异, 故可构造无穷规约序列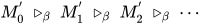 其中
其中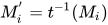 (
(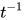 为将表达式中所有
为将表达式中所有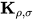 项替换为标识符
项替换为标识符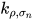 ), 故有
), 故有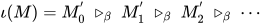 为无穷规约序列, 即
为无穷规约序列, 即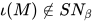 与引理4矛盾, 故
与引理4矛盾, 故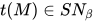 .
.
证毕.
定理2.1: 强正规化定理(strong normalization theorem)
简单带类型的λ-calculus具有强规范性(strong normalization). 即所有简单带类型的λ-calculus表达式均是强规范化的,
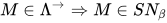 .
.证明: 若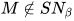 , 由
, 由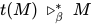 得
得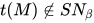 , 与引理6矛盾. 故
, 与引理6矛盾. 故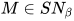 .
.
证毕.
Proof by logical relation
定义: 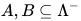 , 表达式集合
, 表达式集合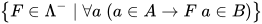 记作
记作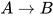 .
.
定义: 对于类型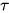 , 表达式集合
, 表达式集合![[\![\tau]\!] \subseteq \Lambda^{-}](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7e8abd3988~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) 为类型
为类型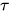 的可计算(computable)集合, 定义如下:
的可计算(computable)集合, 定义如下:
![\begin{align}
&\;[\![\tau]\!]=SN_{\beta}\\
&\;[\![\sigma\to\rho]\!]=[\![\sigma]\!]\to [\![\rho]\!]
\end{align}](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7ebfb94568~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png)
定义: 强正规化集合的子集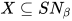 为饱和集合(saturated)当且仅当满足:
为饱和集合(saturated)当且仅当满足:
- 对于
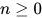 ,
, 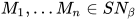 , 有
, 有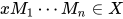
- 对于
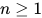 ,
, 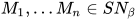 , 有
, 有![M_0[M_1/x]M_2\cdots M_n\in X\Rightarrow (\lambda x.M_0)M_1M_2\cdots M_n\in X](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7ebfddd450~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png)
定义: 所有饱和集合的集合记作为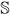 , 即
, 即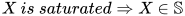 或
或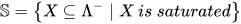 .
.
引理8: 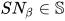 .
.
证明: 显然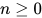 ,
, 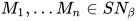 , 有
, 有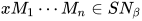 .
. 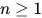 , 显然有
, 显然有![(\lambda x.M_0)M_1M_2\cdots M_n\;\triangleright_{\beta}\;M_0[M_1/x]M_2\cdots M_n](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7ebff5a6f8~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) , 故
, 故![M_0[M_1/x]M_2\cdots M_n\in SN_{\beta}\Rightarrow (\lambda x.M_0)M_1M_2\cdots M_n\in SN_{\beta}](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7e8b1ea74e~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) .
.
证毕.
引理9: 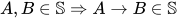 .
.
证明:
若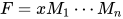 (其中
(其中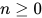 ,
, 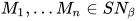 ), 有
), 有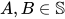 , 令
, 令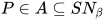 , 那么
, 那么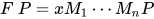 , 其中
, 其中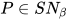 故由
故由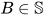 定义得
定义得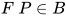 , 因此
, 因此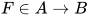 .
.
若
![F=M_0[M_1/x]M_2\cdots M_n](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7e8b56329f~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) (其中
(其中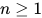 ,
, 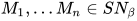 )且
)且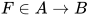 , 令
, 令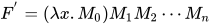 , 由
, 由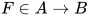 得, 对于
得, 对于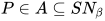 有
有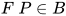 , 又有
, 又有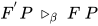 , 即
, 即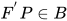 , 故
, 故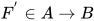 .
.证毕.
引理10: ![\sigma\in\Pi\Rightarrow [\![\sigma]\!]\in\mathbb{S}](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7e968a662c~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) .
.
证明: 对![\ [\![\sigma]\!]](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7ec05150b5~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) 做结构归纳.
做结构归纳.
若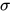 为类型标识符, 根据定义
为类型标识符, 根据定义![\ [\![\sigma]\!]=SN_{\beta}](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7ebc95a0af~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) , 由引理8得
, 由引理8得![\ [\![\sigma]\!]\in\mathbb{S}](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7ec058fd00~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) .
.
若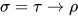 ,
, ![\ [\![\sigma]\!]=[\![\tau]\!]\to [\![\rho]\!]](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7ec0644ea5~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) , 由归纳假设得
, 由归纳假设得![\ [\![\tau]\!],[\![\tau]\!]\in \mathbb{S}](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7ebca2e805~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) , 又由引理9得
, 又由引理9得![[\![\tau]\!]\to [\![\rho]\!]\in \mathbb{S}](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7ec07808ff~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) .
.
证毕.
定义: 求值(valuation)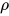 为标识符到表达式上的映射
为标识符到表达式上的映射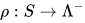 .
.
部分替换记号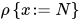 为:
为:
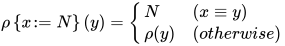
定义: 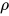 为标识符上的求值,
为标识符上的求值, ![\ [\![M]\!]_{\rho}=M[\rho(x_1)/x_1,\cdots,\rho(x_n)/x_n]](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7ebccc0f04~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) 其中
其中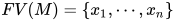 .
.
定义: 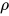 为标识符上的求值,
为标识符上的求值, 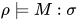 当且仅当
当且仅当![\;[\![M]\!]_{\rho}\in[\![\sigma]\!]](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7ebcdf3e7f~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) ;
; 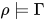 当且仅当
当且仅当![\ \forall (x:\sigma)\in\Gamma\quad(\rho(x)\in[\![\sigma]\!])](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7ec09fc723~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) .
.
定义: 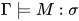 当且仅当
当且仅当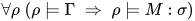 .
.
引理11: Soundness
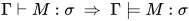
证明: 对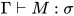 的推导做结构归纳.
的推导做结构归纳.
若推导为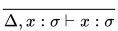 , 其中
, 其中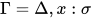 ,
, 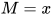 ,
, 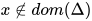 . 若
. 若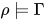 则有
则有![\;[\![x]\!]_{\rho}=\rho(x)\in[\![\sigma]\!]](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7ec16e4db0~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) , 即
, 即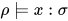 , 故
, 故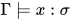 .
.
若推导为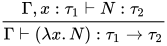 , 其中
, 其中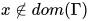 ,
, 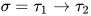 ,
, 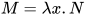 . 不妨设
. 不妨设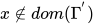 , 若
, 若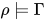 , 令
, 令![P\in [\![\tau_1]\!]](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7ec3263516~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) , 那么有
, 那么有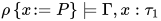 . 根据归纳假设有
. 根据归纳假设有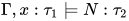 那么有
那么有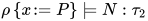 即
即![\ [\![N]\!]_{\rho\{x\!:=P\}}\in [\![\tau_2]\!]](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7ec19f96af~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) .
.
![\begin{align}
\;[\![\lambda x.N]\!]_{\rho}P\;&\equiv\; (\lambda x.N)[\rho(x_1)/x_1,\cdots,\rho(x_n)/x_n]P\\
&\triangleright_{\beta}\;N[\rho(x_1)/x_1,\cdots,\rho(x_n)/x_n,P/x]\\
&\equiv \;[\![N]\!]_{\rho\{x\!:=P\}}
\end{align}](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7ec1a09611~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png)
又有![\;[\![N]\!]_{\rho\{x\!:=P\}}\in [\![\tau_2]\!]\in\mathbb{S}](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7ec3458115~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) , 其中
, 其中![[\![\lambda x.N]\!]_{\rho}P\;\triangleright_{\beta}\;[\![N]\!]_{\rho\{x\!:=P\}}](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7ec3433b4c~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) 故
故![\ [\![\lambda x.N]\!]_{\rho}P\in[\![\tau_2]\!]](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7ec1a04232~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) . 又有
. 又有![P\in [\![\tau_1]\!]](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7ec35b7dea~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) , 因此可得
, 因此可得![\;[\![\lambda x.N]\!]_{\rho}\in[\![\tau_1\to\tau_2]\!]](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7ec35bfeb8~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) , 即
, 即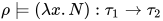 , 故
, 故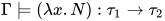 .
.
若推导为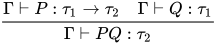 , 其中
, 其中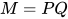 . 若
. 若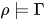 , 根据归纳假设有
, 根据归纳假设有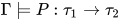 与
与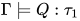 即
即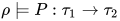 和
和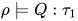 , 那么有
, 那么有![\;[\![P]\!]_{\rho}\in[\![\tau_1]\!]\to[\![\tau_2]\!]](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7ec1ef4ad6~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) 和
和![\;[\![Q]\!]_{\rho}\in[\![\tau_1]\!]](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7ec1e2463d~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) , 故
, 故![\;[\![PQ]\!]_{\rho}=[\![P]\!]_{\rho}[\![Q]\!]_{\rho}\in[\![\tau_2]\!]](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7ec38fec69~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) , 即
, 即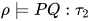 , 故
, 故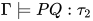 .
.
根据归纳法得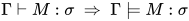 .
.
证毕.
定理2.2: 强正规化定理(strong normalization theorem)
简单带类型的λ-calculus具有强规范性(strong normalization). 即所有简单带类型的λ-calculus表达式均是强规范化的, 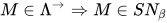 .
.
证明: 由引理11(Soundness)得, 由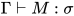 得
得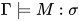 , 取求值
, 取求值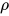 为
为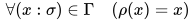 , 显然
, 显然![\rho(x)\in [\![\tau_2]\!]\in\mathbb{S}](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7ec2069cf5~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) 即
即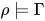 . 由
. 由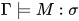 得
得![\;[\![M]\!]_{\rho}\in[\![\sigma]\!]](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7ec3b8cd2f~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) , 其中
, 其中![\ [\![M]\!]_{\rho}=M](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7ec21b88ef~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) ,
, ![\;[\![\sigma]\!]\subseteq SN_{\beta}](https://p1-jj.byteimg.com/tos-cn-i-t2oaga2asx/gold-user-assets/2018/11/30/16762f7ec3c50cc3~tplv-t2oaga2asx-jj-mark:3024:0:0:0:q75.png) , 故
, 故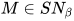 .
.
证毕.
推论1: 所有在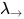 中typable的表达式构成的集合为无类型λ-calculus表达式的真子集.
中typable的表达式构成的集合为无类型λ-calculus表达式的真子集.
证明: 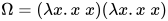 在
在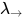 à la Curry中非可类型化(untypable)
à la Curry中非可类型化(untypable)
由定理2(强正规化定理)简单带类型的λ-calculus系统具有强规范性, 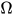 显然不具有normal form. 若
显然不具有normal form. 若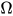 可类型化, 则
可类型化, 则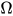 具有一个normal form. 矛盾.
具有一个normal form. 矛盾.
证毕.
推论2: 不动点组合子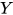 在
在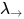 à la Curry中非可类型化(untypable), 即在
à la Curry中非可类型化(untypable), 即在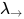 à la Curry中无法构建不动点组合子.
à la Curry中无法构建不动点组合子.
证明: 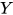 满足
满足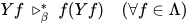 , 取
, 取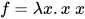 . 显然
. 显然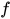 为可类型化的, 若
为可类型化的, 若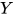 为可类型化的, 而显然
为可类型化的, 而显然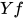 不具有normal form, 类似证明推论1, 可得矛盾. 故
不具有normal form, 类似证明推论1, 可得矛盾. 故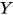 在
在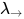 中非可类型化.
中非可类型化.
证毕.
对于不动点组合子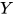 在简单带类型λ-calculus无法构造, 直接的原因是在不动点组合子
在简单带类型λ-calculus无法构造, 直接的原因是在不动点组合子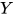 的构造中, 必然会遇到自我调用, 例如
的构造中, 必然会遇到自我调用, 例如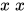 , 其类型推导为:
, 其类型推导为:
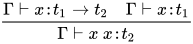
对于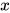 的类型实质上是递归类型
的类型实质上是递归类型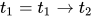 , 在简单带类型λ-calculus系统中不具有此种类型表达.
, 在简单带类型λ-calculus系统中不具有此种类型表达.
为了在带类型λ-calculus表达递归, 一个解决方式是将不动点组合子在表达式层面上引入.
定义: 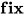 表达式
表达式
- β-规约规则:
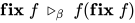 .
. - 类型性规则(typability):
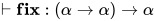 .
.
注: 在将不动点组合子加入到简单带类型λ-calculus后, 其规范性将会被破坏. 更深层次的原因可以追溯至由递归类型引入的悖论, 参见Girard悖论.
类型检查与重建(Type checking and reconstruction)
定义: 在类型系统上的三类问题
- 类型检查(type checking) 给定前提
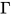 , 表达式
, 表达式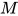 与类型
与类型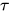 , 确定
, 确定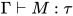 是否成立.
是否成立. - 类型重建(type reconstruction)或类型推导(type inference) 给定前提
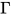 与表达式
与表达式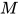 , 确定是否存在类型
, 确定是否存在类型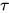 使得
使得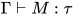 是否成立.
是否成立. - 类型居留(type inhabitation) 给定前提
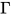 与类型
与类型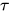 , 确定是否存在表达式
, 确定是否存在表达式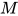 , 使得
, 使得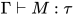 是否成立. (这里对居留问题不做深入介绍)
是否成立. (这里对居留问题不做深入介绍)
注: 从直觉上来说类型检查会比类型重建更容易, 但在更为丰富的类型系统中, 类型检查并不比类型重建更容易, 反而类型重建可以问题可以规约成类型检查.
对于检查表达式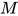 (其中
(其中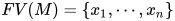 ), 确定是否存在类型
), 确定是否存在类型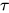 在
在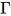 中使得
中使得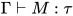 是否成立可以规约为确定
是否成立可以规约为确定
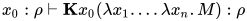
是否成立(即类型检查).
对于简单带类型λ-calculus的类型检查与类型重建问题, 首先从一阶合一化(first-order unification)开始介绍.
First-order unification
定义: 一阶标署(first-order signatures) 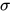
其中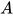 为全集,
为全集, 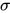 为
为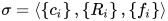
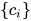 为常量符号集合,
为常量符号集合, 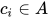 .
.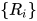 为
为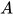 上的
上的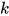 元关系, 即
元关系, 即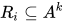 .
.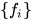 为
为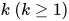 元函数,
元函数, 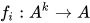 .
.
其中0元函数视作为常量. 若标署中不包含关系则称该标署为代数标署(algebraic signatures), 在合一问题里只考虑代数标署.
定义: 在一阶标署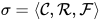 上的代数项(algebraic term)
上的代数项(algebraic term)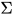 为
为
- 常量
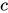 (
(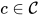 ).
).  , 其中
, 其中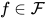 ,
, 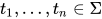 .
.
即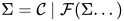 .
.
定义: 方程(equation)为一对代数项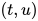 , 写作
, 写作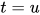 . 方程组(system of equations)为方程的有限集合. 方程中的标识符称为未知元(unknowns).
. 方程组(system of equations)为方程的有限集合. 方程中的标识符称为未知元(unknowns).
定义: 替换(substitution)为从代数项至代数项的映射
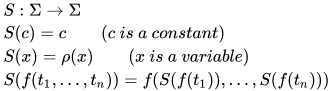
其中对于标识符, 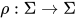 为对该标识符的求值(valuation).
为对该标识符的求值(valuation).
定义: 方程的解(solution of an equation)为替换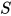 , 其中求值
, 其中求值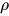 满足对于方程
满足对于方程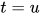 有
有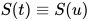 . 方程组的解为替换
. 方程组的解为替换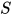 均为方程组中每个方程的解.
均为方程组中每个方程的解.
方程的解的一个例子:
对于方程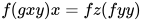 , 其解为
, 其解为
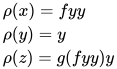
定义: 对于方程组, 称其为已解(solved form)当且仅当
- 所有方程均为
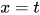 形式, 其中
形式, 其中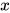 为标识符.
为标识符. - 对于一个在方程左边的标识符, 其不出现在方程组中的任何其他位置.
对于没有出现在方程左边的标识符, 则称之为未定元(undefined).
对于一个已解的方程, 有解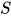 :
:
其中显然有.
定义: 对于方程组, 称其为不一致的(inconsistent)当且仅当存在以下几种形式的方程
, 其中
.
或
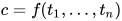 , 其中
, 其中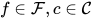 .
.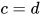 , 其中
, 其中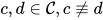 .
., 其中
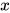 出现在
出现在 中.
中.
对于一个不一致的方程组, 显然其无解.
定义: 两个方程组与
为等价的(equivalent)当且仅当其解相同, 记作
.
定义: 对于给定方程组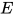 , 判定该方程组
, 判定该方程组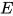 是否存在等价方程组
是否存在等价方程组,
为已解的(solved form)或不一致的(inconsistent). 该类问题为一阶合一问题(first-order unification).
Robinson's algorithm
定义: 方程符号替换, 表示将方程中出现的标识符
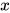 替换为代数项
替换为代数项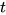 ; 定义替换
; 定义替换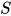 其中
其中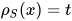 , 即
, 即.
定义: 对于方程组的变换操作
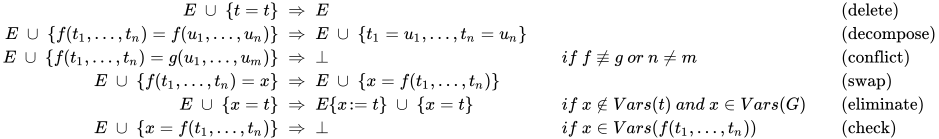
其中 表示方程组不一致.
表示方程组不一致.
引理12: 方程组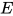 经过上述删除(delete)到检查(check)变换操作后得到方程组
经过上述删除(delete)到检查(check)变换操作后得到方程组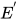 , 有
, 有.
证明: 对于矛盾(conflict)和检查(check)变换, 显然原方程组和变换后方程组均不一致, 故等价即.
对于交换(swap)变换, 显然交换方程两边后方程解保持不变, 即.
对于删除(delete)变换, 方程对于任意解均成立, 删去后方程解保持不变, 即
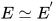 .
.
对于分解(decompose)变换, 若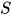 为方程组
为方程组的解, 即有
, 又由替换定义有
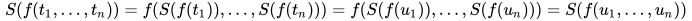 , 故
, 故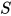 为方程
为方程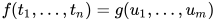 的解, 故
的解, 故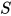 同样为方程组
同样为方程组的解, 反之亦然, 即
,
对于消除(eliminate)变换, 若为方程组
的解, 即有
, 另外对于方程组
,
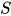 为其解且
为其解且, 根据替换的定义, 在方程中替换标识符和代数项
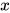 与
与解亦然成立(严格证明可由归纳给出),
为方程组
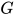 的解, 即
的解, 即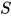 为方程组
为方程组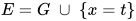 的解, 反之亦然, 故
的解, 反之亦然, 故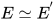 .
.
证毕.
引理13: 对于任意方程组, 只能应用有限次上述删除(delete)到检查(check)变换操作.
证明: 对于矛盾(conflict)和检查(check)变换, 显然进行一次变换后得到, 无法继续进行变换.
对于剩余4种变换, 定义三元组, 其中
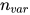 表示方程组中重复出现的标识符的数量,
表示方程组中重复出现的标识符的数量, 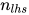 表示在方程左边函数符号以及常量的数目,
表示在方程左边函数符号以及常量的数目,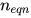 表示方程组中方程的数目.
表示方程组中方程的数目.
其中在三元组上定义字典序, 即三元组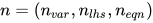 和
和,
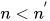 当且仅当
当且仅当或
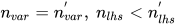 或
或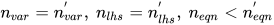 ; 若
; 若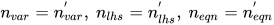 则为
则为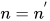 ; 若非
; 若非与
则为
. 显然三元组上的字典序是良基关系, 且是全序关系.
设变换前的三元组为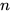 , 变换后的三元组为
, 变换后的三元组为.
对于进行交换(swap)变换, 与
保持不变,
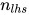 减小, 故
减小, 故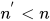 .
.
对于进行删除(delete)变换, 与
不增加,
减小, 故
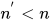 .
.
对于进行分解(decompose)变换, 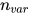 保持不变,
保持不变, 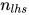 减小, 故
减小, 故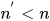 .
.
对于进行消除(eliminate)变换, 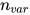 减少(
减少(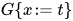 中标识符
中标识符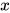 被替换, 变换后方程组中标识符
被替换, 变换后方程组中标识符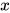 只出现一次, 在
只出现一次, 在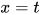 中), 故
中), 故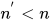 .
.
由上, 对方程组进行交换, 删除, 分解, 消除变换后均有
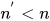 , 且三元组上定义字典序是良基的. 故对于任意的方程组均只能进行有限次变换.
, 且三元组上定义字典序是良基的. 故对于任意的方程组均只能进行有限次变换.证毕.
定理3: Robinson's algorithm
对于任意方程组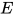 , 在通过有限次上述删除(delete)到检查(check)变换操作后得到等价方程组
, 在通过有限次上述删除(delete)到检查(check)变换操作后得到等价方程组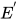 ,
, 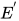 为已解的(solved form)或不一致的(inconsistent).
为已解的(solved form)或不一致的(inconsistent).
证明: 对于方程组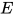 , 若其为非已解的且非不一致的, 根据定义, 可对方程进行删除(delete)到检查(check)的变换操作, 由引理12与引理13得, 在有限次变换操作后(即算法必停机), 无法再继续进行变换, 得到的等价方程组
, 若其为非已解的且非不一致的, 根据定义, 可对方程进行删除(delete)到检查(check)的变换操作, 由引理12与引理13得, 在有限次变换操作后(即算法必停机), 无法再继续进行变换, 得到的等价方程组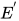 为已解的或不一致的.
为已解的或不一致的.
证毕.
推论3: 一阶合一问题(first-order unification)是可判定的(decidable).
证明: 由Robinson's algorithm即得.
证毕.
定义: 替换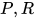 , 复合替换
, 复合替换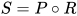 为
为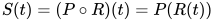 . 其中称替换
. 其中称替换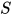 为替换
为替换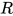 的一个实例(instance). 定义偏序关系
的一个实例(instance). 定义偏序关系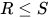 当且仅当
当且仅当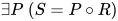 , 即
, 即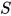 为
为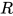 的实例.
的实例.
定义: 替换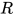 为方程组
为方程组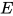 的解,
的解, 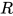 为主解(principal solution)则对于任意替换
为主解(principal solution)则对于任意替换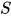 为方程组
为方程组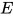 的解当且仅当
的解当且仅当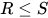 .
.
方程的主解的一个例子:
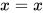
其主解为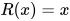 , 另外还有解
, 另外还有解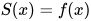 , 其中有
, 其中有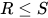 .
.
引理14: 若方程组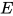 存在解, 则其存在唯一主解(principal solution).
存在解, 则其存在唯一主解(principal solution).
证明: 对于方程组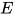 , 使用Robinson's algorithm, 得到等价已解方程组
, 使用Robinson's algorithm, 得到等价已解方程组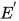 , 方程组
, 方程组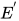 中的方程均形如
中的方程均形如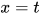 . 令替换
. 令替换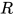 中的求值
中的求值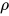 为
为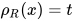 , 显然替换
, 显然替换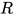 为方程组的解, 有
为方程组的解, 有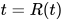 .
.
若替换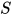 有
有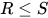 , 则
, 则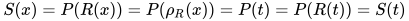 , 故替换
, 故替换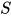 为方程的解.
为方程的解.
若替换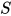 为方程的解, 有
为方程的解, 有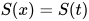 , 又有
, 又有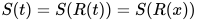 即
即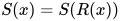 , 故
, 故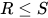 . 因此有解
. 因此有解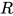 为方程的主解.
为方程的主解.
显然对于由Robinson's algorithm得到的替换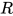 , 其为唯一的.
, 其为唯一的.
证毕.
Type checking and reconstruction algorithm
定义: 对于给定的λ-表达式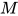 , 构造关于
, 构造关于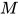 的方程组
的方程组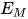 与类型
与类型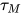 .
.
- 若
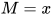 (
(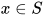 ), 构造
), 构造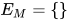 ,
, 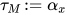 其中
其中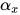 为一个新的类型未定元.
为一个新的类型未定元. - 若
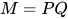 , 构造
, 构造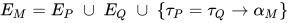 ,
, 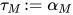 其中
其中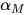 为一个新的类型未定元.
为一个新的类型未定元. - 若
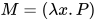 , 构造
, 构造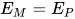 ,
, 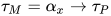 .
.
注: 在此的一阶标署中的函数唯有二元函数 , 将
, 将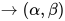 记作
记作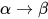 .
.
定理4: 类型检查与重建(type checking and reconstruction)
- 若
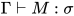 , 对于方程组
, 对于方程组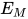 存在解
存在解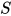 满足
满足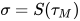 与
与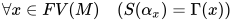 .
. - 若替换
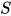 为方程组
为方程组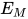 的解且
的解且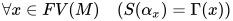 , 则有
, 则有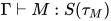 .
.
证明:
1. 对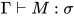 推导做结构归纳.
推导做结构归纳.
若推导为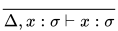 , 其中
, 其中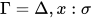 ,
, 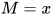 ,
, 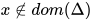 , 且
, 且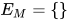 ,
, 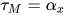 显然解
显然解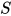 为
为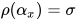 , 即
, 即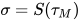 .
.
若推导为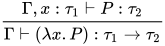 , 其中
, 其中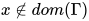 ,
, 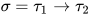 ,
, 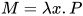 , 且
, 且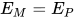 ,
, 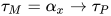 . 不妨设
. 不妨设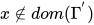 , 根据归纳假设有对于
, 根据归纳假设有对于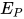 有解
有解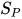 , 令替换
, 令替换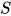 为:
为:
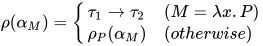
显然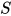 为
为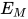 的解, 同时有
的解, 同时有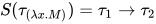 .
.
若推导为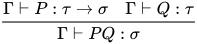 , 其中
, 其中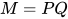 , 且
, 且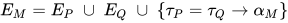 ,
, 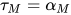 . 根据归纳假设有对于
. 根据归纳假设有对于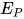 与
与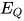 有解
有解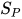 与
与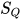 , 其中
, 其中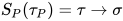 与
与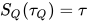 , 那么构造替换
, 那么构造替换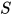 为:
为:
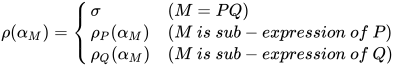
显然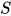 为
为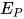 与
与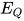 的解;
的解;
对于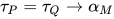 , 有:
, 有:
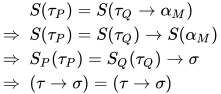
故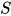 为方程
为方程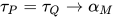 的解, 即替换
的解, 即替换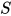 为
为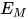 的解, 同时有
的解, 同时有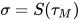 .
.
故由归纳得原命题成立.
2. 对表达式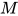 做结构归纳.
做结构归纳.
若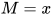 ,
, 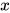 为任意标识符, 那么有
为任意标识符, 那么有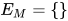 ,
, 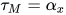 , 原命题显然成立;
, 原命题显然成立;
若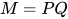 , 那么有
, 那么有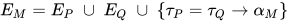 ,
, 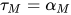 , 替换
, 替换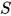 为方程组
为方程组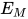 的解, 故
的解, 故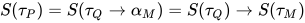 , 同时
, 同时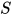 亦为方程
亦为方程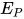 与
与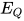 的解, 根据归纳假设有
的解, 根据归纳假设有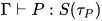 即
即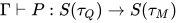 与
与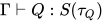 , 因此
, 因此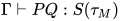 , 原命题成立;
, 原命题成立;
若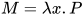 , 那么有
, 那么有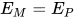 ,
, 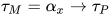 , 替换
, 替换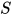 为方程组
为方程组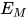 的解即
的解即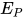 的解, 根据归纳假设有
的解, 根据归纳假设有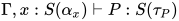 , 故有
, 故有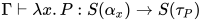 , 即
, 即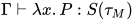 , 原命题成立;
, 原命题成立;
故由归纳得原命题成立.
证毕.
推论4: Type checking and reconstruction algorithm
简单带类型λ-calculus的类型检查与重建是可判定的(decidable).
证明: 由定理4, 类型检查与重建可规约为一阶合一问题, 对于表达式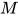 使用Robinson's algorithm求解方程组
使用Robinson's algorithm求解方程组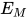 . 由推论3得类型检查与重建是可判定的.
. 由推论3得类型检查与重建是可判定的.
证毕.
定义: 若给定表达式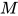 , 对于任何前提
, 对于任何前提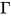 与类型
与类型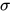 满足
满足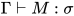 均存在替换
均存在替换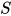 使得
使得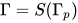 与
与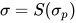 , 且有
, 且有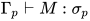 , 则类型
, 则类型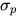 称为主类型(principal type).
称为主类型(principal type).
(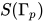 表示对于任意
表示对于任意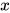 均有
均有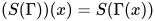 )
)
主类型的一个例子:
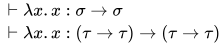
其中 为
为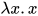 的主类型. 对于
的主类型. 对于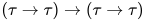 替换
替换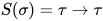 .
.
推论5: 若表达式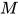 可类型化(typable), 则其存在唯一的主类型.
可类型化(typable), 则其存在唯一的主类型.
证明: 由定理4(类型检查与重建)与引理14得主类型唯一.
证毕.
一阶合一问题在计算机科学与逻辑中广泛出现, 简单带类型λ-calculus的类型检查与重建为其应用之一. 例如使用合一算法可以实现树形数据结构的匹配, 例如嵌套模式匹配等等. 更多的应用就等大家取慢慢发现啦.
这篇文章介绍了不少内容, 篇幅比较长, 感谢大家的耐心阅读啦喵~
最後感謝莎莎喵一直以來的支持