看到
的文章
一道高三的数列题 之后,研究了一会,发现了另一种解法
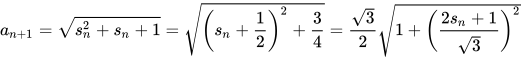
所以
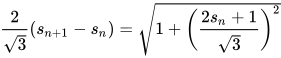
令
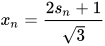
则
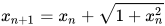
做三角换元,令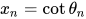 ,则
,则
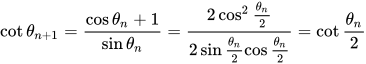
所以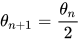 ,又因为
,又因为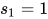 ,所以
,所以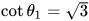 ,
,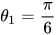 ,
,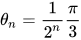
所以
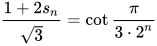
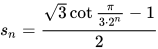
所以
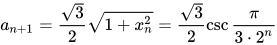
可以验证这个式子对n = 0也成立,所以
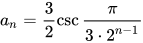
补充:其实是在尝试别的方法的时候发现了这条路,然后重新修正了过程,直接一次找到这个方法是很困难的,对三角换元以及公式的掌握程度要求也很高,比如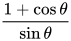 ,而且如果按照常规用
,而且如果按照常规用 换元的话,这里遇到的是
换元的话,这里遇到的是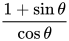 ,处理起来会更麻烦:
,处理起来会更麻烦:
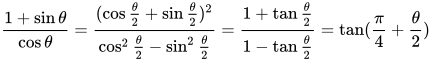
如果用上复数的话反而可以有通用方法(虽然复杂一些),还是复数大法好
另外:注意到我们通过换元将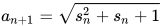 变成了
变成了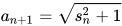 的形式,实际上对于
的形式,实际上对于
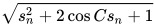
都可以用相似的方法进行变形
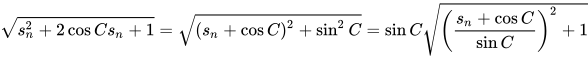
本质上来说都是余弦定理……