数据结构基础--链表

催眠
270 阅读7分钟
原文链接： www.jianshu.com

目录

  • 基本性质
  • 链表的分类
    • 按连接方向分类
    • 按照有无循环分类
  • 链表问题代码实现的关键点
  • 链表插入和删除的注意事项
  • 链表翻转
  • 向一个有序的环境链表中插入一个节点，并保持依旧有序
  • 对于一个单链表，在不给定head的情况下删除指定node。要求时间复杂度O(1)
  • 给定一个链表，与一个数组num。要求实现荷兰国旗
  • 给定两个有序链表的head，打印共同部分
  • 给定一个单链表的head，实现一个调整链表的函数，使得每K个节点之间逆序，如果最后不足K个，则不调整
  • 判断一个链表是否为回文结构
  • 判断一个单链表是否有环，如有则返回入环节点。时间复杂度O(N)，额外空间复杂度O(1)
  • 两个无环单链表是否相交，时间复杂度O(N+M)，额外空间复杂度O(1)
  • 判断两个有环单链表是否相交，时间复杂度O(N+M)，额外空间复杂度O(1)
  • 判断两个链表是否相交，并返回第一个相交的节点

基本性质

  • 链表问题算法难度不高，但考察代码的实现能力
  • 链表和数组一样，都是一种线性结构
  1. 数组是物理地址上一段连续的存储空间。
    可以通过下标直接获取元素
    当内容超出容量时需要重新定义数组。
  2. 链表空间不一定保持联系，为临时分配的。
    只能从链表的头部开始一个一个查找
    增删的效率高于数组，因为不需要更改内存结构

链表的分类

  • 按连接方向分类
  1. 单链表
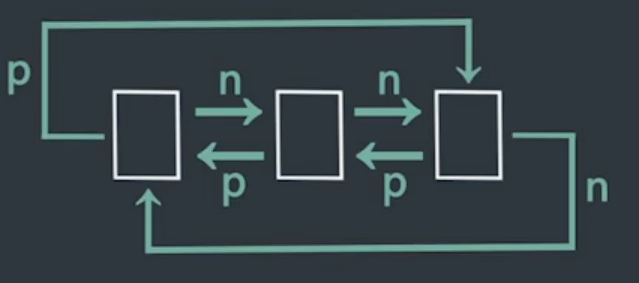
    每个节点只能通过next指针，指向下一个节点。
  2. 双链表
    除了next指针之外，还有一个prev指针指向其上一个节点。
  • 按照有无循环分类
  1. 普通链表
    头无prev，尾无next。

  1. 循环链表
    首尾相接的链表。
    最后一个节点的next指针指向其第一个节点
    对于双链表，其第一个节点的prev指针指向最后一个节点。


链表问题代码实现的关键点

  • 链表调整函数的返回值，往往是节点类型

链表在调整过程中往往遇到改变头部的情况，如果头节点被改变则需要返回一个新头部。

  • 在调整链表的过程中，先采用画图的方式理清逻辑

注意那些指针变化了，同时注意对前后节点的影响。

  • 边界条件的处理

头节点，尾节点，空节点的特殊处理。

链表插入和删除的注意事项

  • 特殊处理链表为空或长度为1
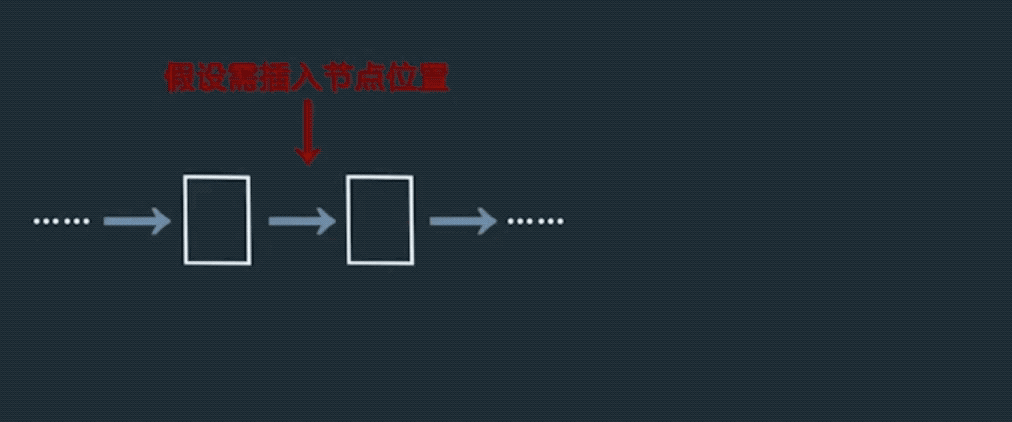
  • 插入过程的调整

取得前后节点，将前节点的next指向新节点，新节点的next指向后节点。

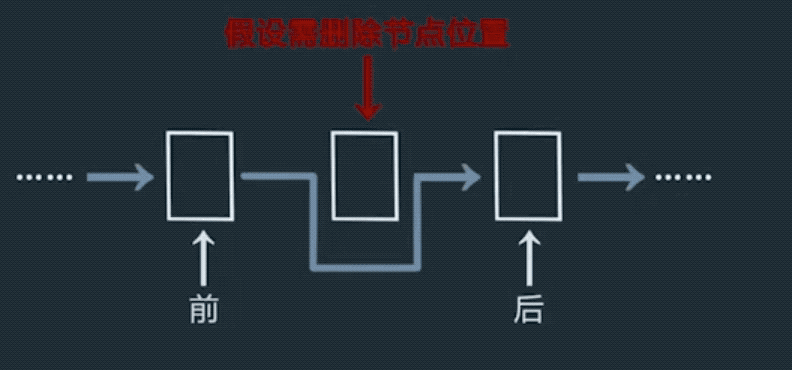
  • 删除过程的调整

取得前后节点，将前一个节点的next指针指向后一个节点。

  • 头尾插入或删除

在逻辑的设计上应该考虑空节点的情况

链表翻转

  • 特殊处理链表为空或长度为1
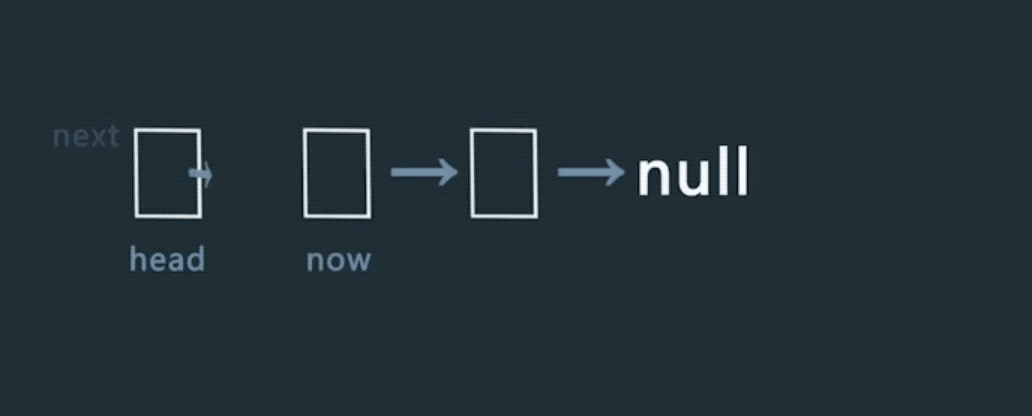
  • 单链表的翻转

已翻转的头节点head，下一个节点now

  1. 将now节点的next指向head
  2. 将now节点设置为已翻转部分的新head

需要注意在执行1，2步骤之前需要一个变量来储存原now节点的next节点。
步骤2设置了新的head之后，将该节点作为新的now，继续翻转。

向一个有序的环境链表中插入一个节点，并保持依旧有序。

要求时间复杂度O(N)，额外空间复杂度O(1)。

  • 如果链表为空

让新节点node自己成为环形链表，并返回node即可。

  • 如果链表不为空

令变量prve设为头节点，current设为第二个节点，两个节点同步移动。

  • 当有node<=prve && node>=current，则说明node应该插入二者之间

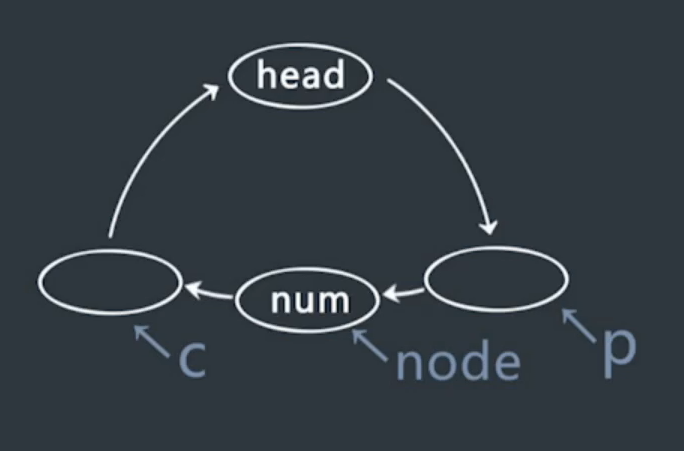
  • 若prve回到head但依旧没有合适的位置插入
    说明node为最大值或最小值，插入head之前即可。
    需要区分为两种情况下是否出现新的head，并返回。

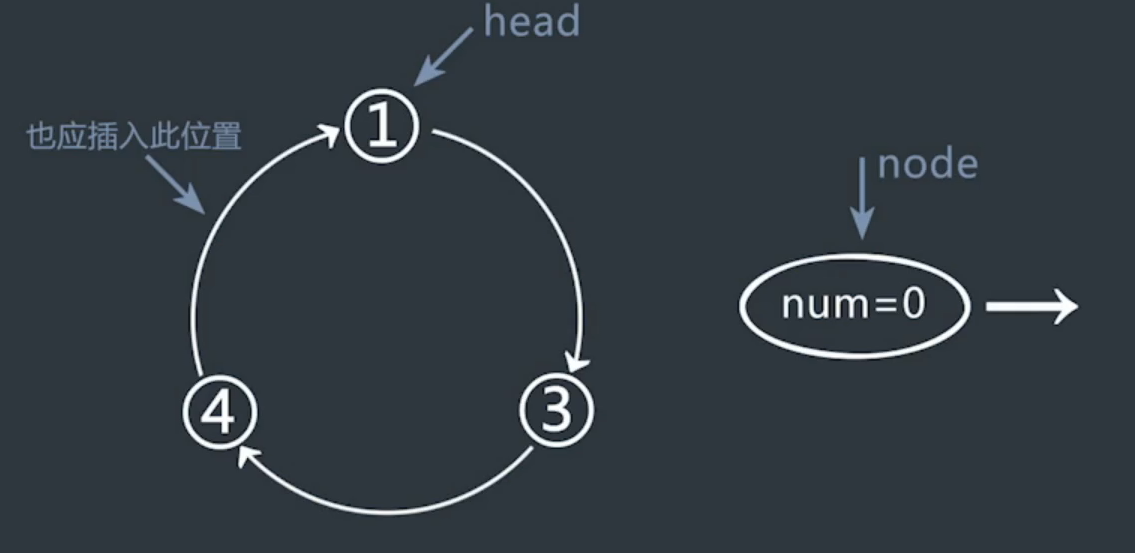
对于一个单链表，在不给定head的情况下删除指定node。要求时间复杂度O(1)

  • 如果node.next不为空，也就是node不是尾节点

如果工程允许，可以将node.next的内容copy到node节点上，变相的删除了node节点的数据。

  • 如果node是尾节点

无法删除

给定一个链表，与一个数组num。要求实现荷兰国旗

  • 将链表遍历成数组，然后进行荷兰国旗排序，最后还原成链表。
  • 遍历链表的过程中使用三个小链表。小于，等于，大于。最后将三个链表串联。

给定两个有序链表的head，打印共同部分

  • 有一个为空直接返回
  • 采用外排的方式，直到有一个为空则停止。

给定一个单链表的head，实现一个调整链表的函数，使得每K个节点之间逆序，如果最后不足K个，则不调整。

  1. 链表为空，长度<k或者k<2
    直接返回
  • 通过栈结构，实现逆序
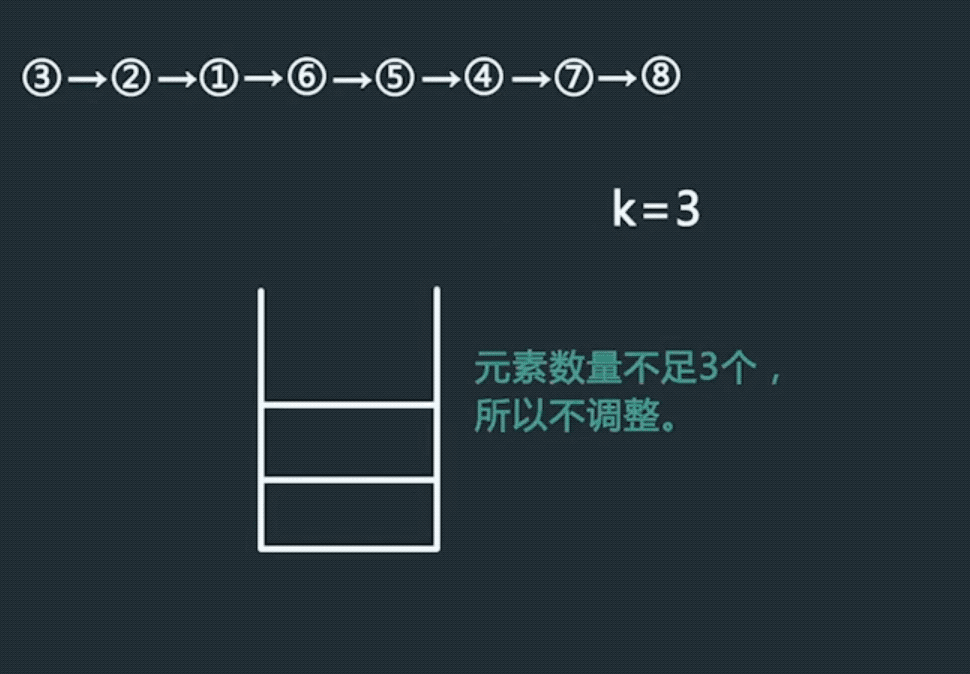
  1. 需要保留上次逆序的最后一位元素，修改其next。
  2. 最后段不足k个，直接不修改。值将上次逆序的最后一个元素next设置好。
  3. 第一组的第一个节点为头节点。
  • 不使用栈结构，手动逆序

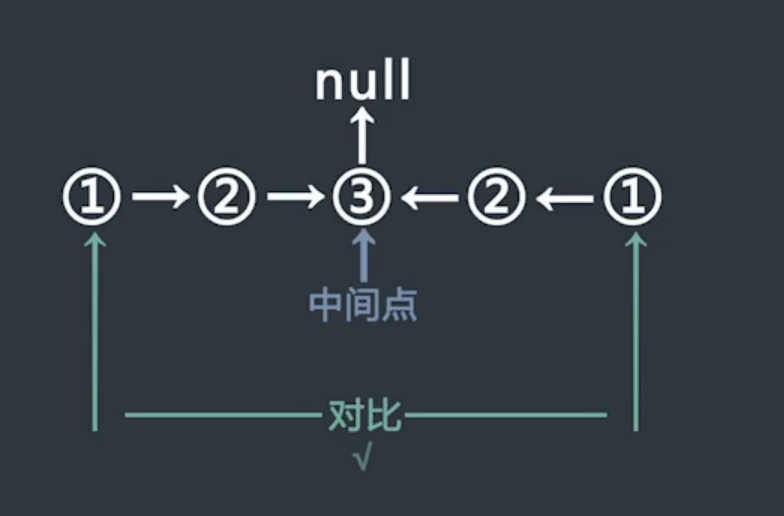
判断一个链表是否为回文结构

  1. 将链表节点依次入栈，在弹出时与原链表依次比对。

  2. 使用快行指针，通过二倍速的方式遍历。依次将慢指针的节点压入栈中，当快节点遍历到末尾时，慢指针正好处于中间位置。
    继续移动慢指针，并与栈中弹出的元素做对比。(需要注意总量的奇偶)


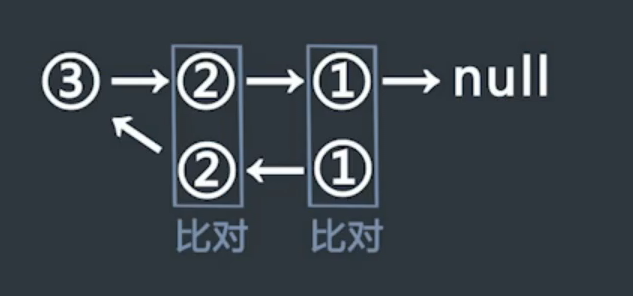
  3. 将后半部分链表进行逆序处理，从两端同时进行遍历比对


判断一个单链表是否有环，如有则返回入环节点。时间复杂度O(N)，额外空间复杂度O(1)

如果不要求额外空间复杂度，可以直接用哈希表比对。

  • 使用快行指针的方式

如果两指针相遇则表示有环，此时将快指针改为1，并从head重新同步移动，相遇处即为入环位置或者还有另一个证明。

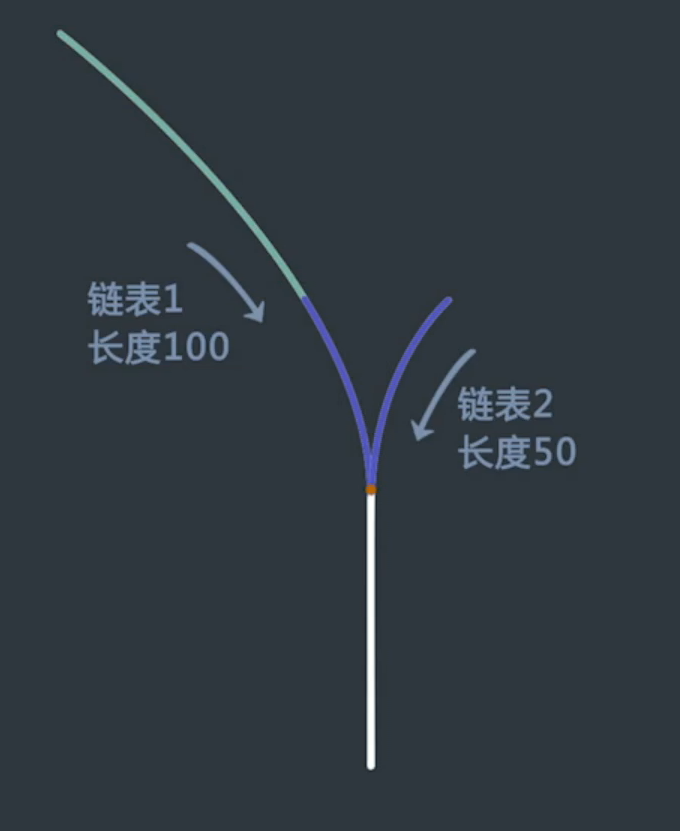
两个无环单链表是否相交，时间复杂度O(N+M)，额外空间复杂度O(1)

先遍历两个链表确定长度，然后另长链表从短链表开始位置与短链表再次同步遍历，查看是否相同。


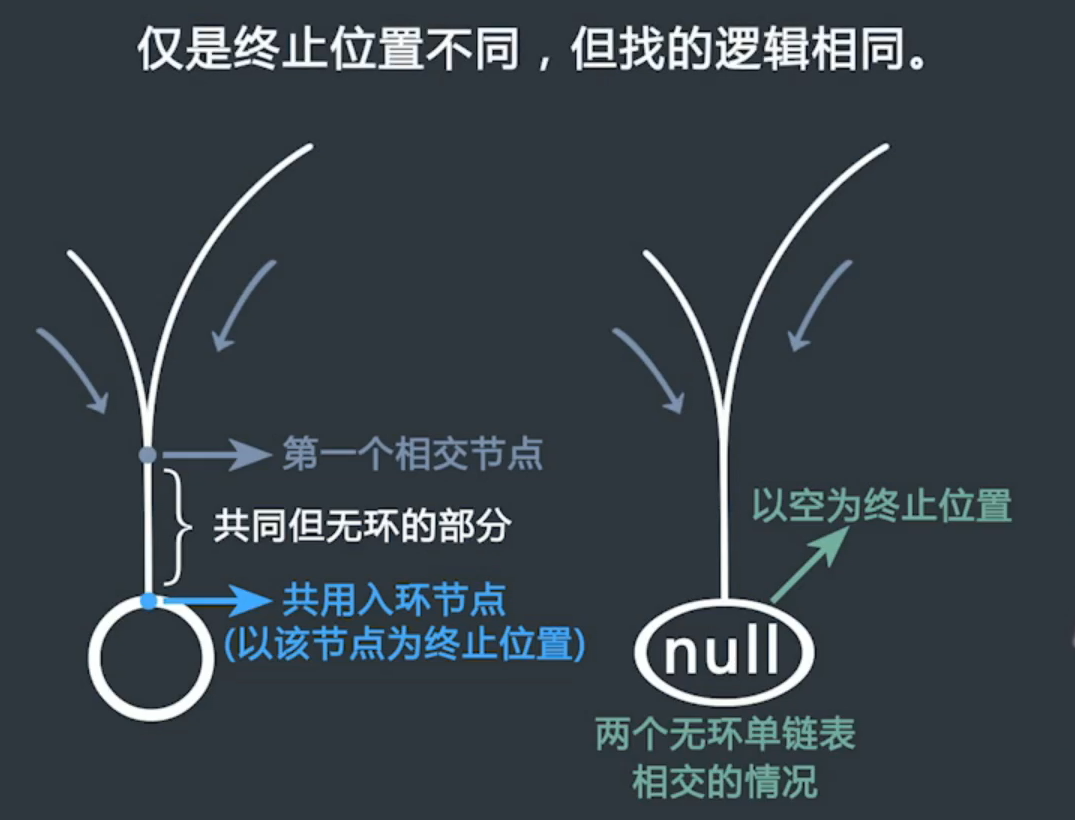
判断两个有环单链表是否相交，时间复杂度O(N+M)，额外空间复杂度O(1)

首先都需要先去定单独的入环节点，然后

  1. 是否入环之前已经相交


  2. 是否入环时才相交，则入环位置节点相同


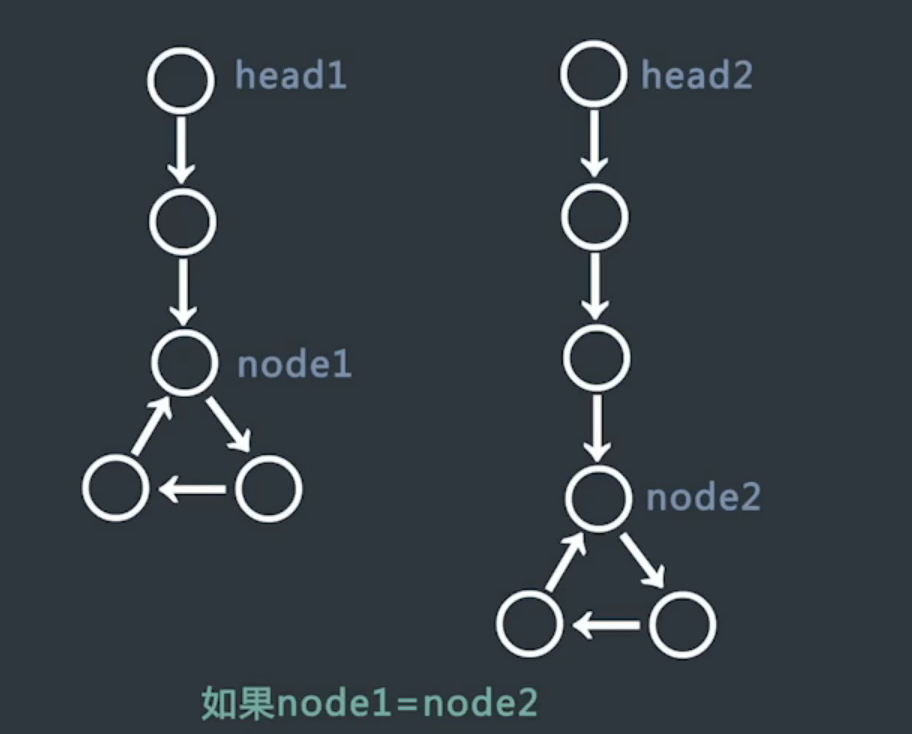
  3. 循环其中一个环，若遇到另一个的入环节点则返回。


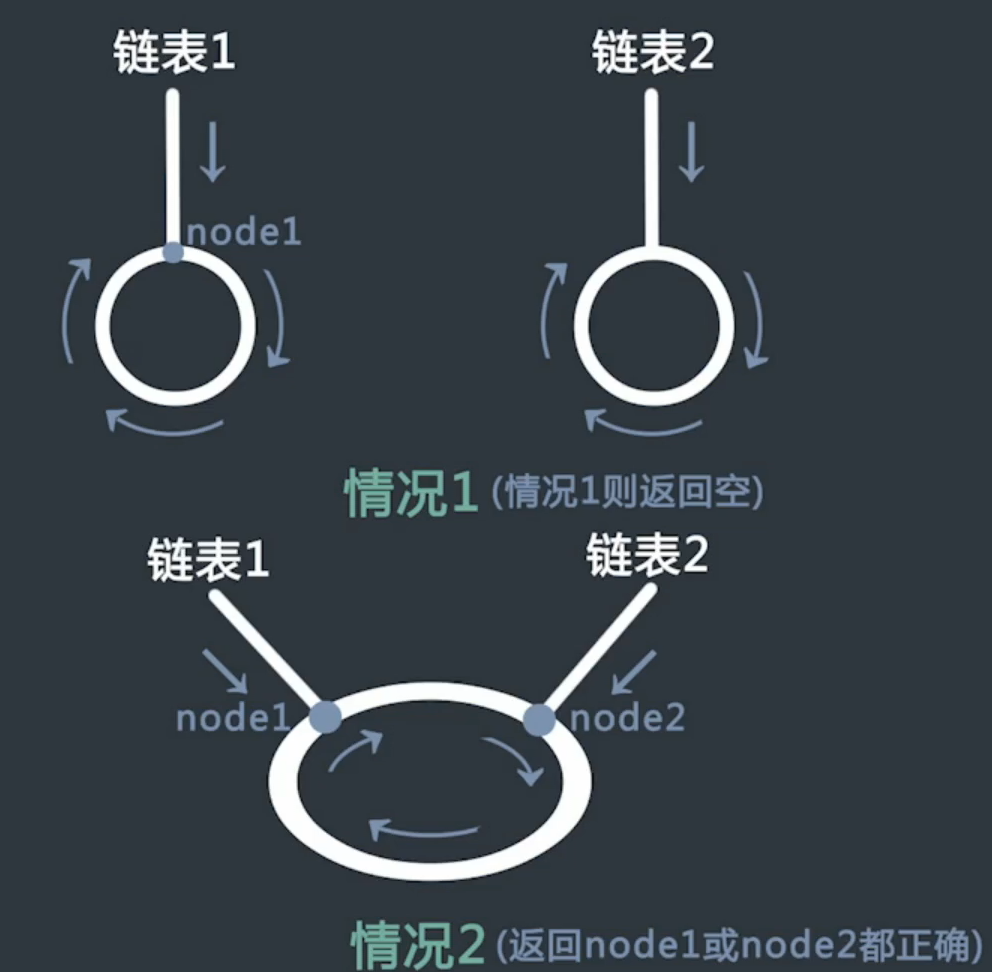
  4. 否则，两链表并未相交

判断两个链表是否相交，并返回第一个相交的节点

  1. 尝试找到各自的入环节点

  2. 若一个有环一个无环，则不相交

  3. 若都为无环，则按照上文《两个无环单链表是否相交》的方式查找

  4. 若都为有环，则按照上文《判断两个有环单链表是否相交》的方式查找

参考资料

左神牛课网算法课

avatar
文章
阅读
粉丝