JavaScript实现《啊哈！算法》中的系列算法

《啊哈！算法》pdf版 下载

第1章 一大波数正在靠近——排序

第1节 最快最简单的排序——桶排序.

var testArr = [3, 5, 3, 5, 9, 7, 6]
// 桶排序---浪费空间，且只能比较自然数，时间复杂度是 O(m+n)
// 需要对数据范围在 0~n 之间的整数进行排序
// skipArr 需要排序的数据组成的数组
function skipSort (n, skipArr) {
  var arr = []
  var sortArr = []
  arr.length = n
  for (let i = 0; i <= n; i++) {
    arr[i] = 0
  }
  for (let j = 0; j < skipArr.length; j++) {
    arr[skipArr[j]]++
  }
  // 从小到大的排序
  // for (let t = 0; t <= n; t++) {
  //   if (arr[t]) {
  //     for (let k = 1; k <= arr[t]; k++) {
  //       sortArr.push(t)
  //     }
  //   }
  // }
  // 从大到小的排序
  for (let t = n; t > 0; t--) {
    if (arr[t]) {
      for (k = 1; k <= arr[t]; k++) {
        sortArr.push(t)
      }
    }
  }
  return sortArr
}

console.log('桶排序:', skipSort(10, testArr))

第2节 邻居好说话——冒泡排序

var testArr = [3, 5, 3, 5, 9, 7, 6]
// 冒泡排序---时间复杂度是O(N的2次方)，执行效率底
// bubbleArr 需要排序的数据组成的数组
function bubbleSort (bubbleArr) {
  var i, j, temp
  for (i = 0; i < bubbleArr.length; i++) {
    for (j = 0; j < bubbleArr.length - 1 - i; j++) {
      // 从小到大的排序
      // if (bubbleArr[j] > bubbleArr[j +1]) {
      //   temp = bubbleArr[j]
      //   bubbleArr[j] = bubbleArr[j + 1]
      //   bubbleArr[j + 1] = temp
      // }
      // 从大到小的排序
      if (bubbleArr[j] < bubbleArr[j +1]) {
        temp = bubbleArr[j]
        bubbleArr[j] = bubbleArr[j + 1]
        bubbleArr[j + 1] = temp
      }
    }
  }
  return bubbleArr
}

console.log('冒泡排序:', bubbleSort(testArr))

第3节 最常用的排序——快速排序

// 快速排序---时间复杂度最差是O(N的2次方)，平均时间复杂度为O(NlogN)
// quickArr 需要排序的数据组成的数组
function quickSort (quickArr, left, right) {
  var i, j, k, temp
  if (left > right) {
    return
  }
  temp = quickArr[left]
  i = left
  j = right
  while (i !== j) {
    // 从小到大的排序
    // while (quickArr[j] >= temp && i < j) {
    //   j--
    // }
    // while (quickArr[i] <= temp && i < j) {
    //   i++
    // }
    // 从大到小的排序
    while (quickArr[j] <= temp && i < j) {
      j--
    }
    while (quickArr[i] >= temp && i < j) {
      i++
    }
    if (i < j) {
      t = quickArr[i]
      quickArr[i] = quickArr[j]
      quickArr[j] = t
    }
  }
  quickArr[left] = quickArr[i]
  quickArr[i] = temp
  quickSort(quickArr, left, i - 1)
  quickSort(quickArr, i + 1, right)
  return quickArr
}

console.log('快速排序:', quickSort(testArr, 0, testArr.length - 1))

第2章 栈、队列、链表

第1节 解密 QQ号——队列

规则是这样的：首先将第 1个数删除，紧接着将第 2 个数放到 这串数的末尾，再将第 3 个数删除并将第 4 个数放到这串数的末尾，再将第 5 个数删除…… 直到剩下最后一个数，将最后一个数也删除。按照刚才删除的顺序，把这些删除的数连在一 起就是真实的QQ啦。

// 队列--先进先出的数据结构

// 加密后的QQ字符串是 6 3 1 7 5 8 9 2 4
const arrAfter = [6, 3, 1, 7, 5, 8, 9, 2, 4];

function getQQ(arrAfter) {
  let middleArr = Object.assign([], arrAfter);
  middleArr.unshift(0);
  let arrBefore = [];
  let head = 1;
  let tail = middleArr.length;
  while (head < tail) {
    arrBefore.push(middleArr[head]);
    head++;
    middleArr.push(middleArr[head]);
    tail++;
    head++;
  }
  return arrBefore;
}

console.log("getQQ:", getQQ(arrAfter)); //  [ 6, 1, 5, 9, 4, 7, 2, 8, 3 ]

第2节 解密回文——栈

// 栈--后进先出的数据结构
// 用来判断回文字符串
function stackFun (stackStr) {
  var stackNewArr = [], len, mid, next, top
  len = stackStr.length
  mid = Math.floor(len / 2 - 1)
  top = 0
  for (var i = 0; i <= mid; i++) {
    stackNewArr[++top] = stackStr[i]
  }
  if (len % 2 === 0) {
    next = mid + 1
  } else {
    next = mid + 2
  }
  for (var j = next; j <= len-1; j++) {
    if (stackStr[j] !== stackNewArr[top]) {
      break
    }
    top--
  }

  if (top === 0) {
    return 'YES'
  } else {
    return 'NO'
  }
}

console.log(stackFun('abeffeba'))

第3节 纸牌游戏——小猫钓鱼

// 纸牌游戏--小猫钓鱼--队列和栈配合使用

// 初始化队列--小哼手里牌的相关信息（先进先出）
const q1 = {
  head : 1,
  tail : 1,
  data: []
}

// 初始化队列--小哈手里牌的相关信息（先进先出）
const q2 = {
  head : 1,
  tail : 1,
  data: []
}

// 初始化栈--桌面上牌的相关信息（先进后出）
const s = {
  top: 0,
  data: []
}

// 初始化用来标记的数组，用来标记哪些牌已经在桌上（桶排序）
const book = []
book.length = 10

for (let i = 1; i <= 9; i++) {
  book[i] = 0
}

// 依次向队列中插入6个数
const arr1 = [2, 4, 1, 2, 5, 6]
const arr2 = [3, 1, 3, 5, 6, 4]

// 小哼手上的6张牌
for (let i = 1; i <= arr1.length; i++) {
  q1.data[q1.tail] = arr1[i - 1]
  q1.tail++
}

// 小哈手上的6张牌
for (let i = 1; i <= arr2.length; i++) {
  q2.data[q2.tail] = arr2[i - 1]
  q2.tail++
}

// 当队列不为空的时候执行循环
while (q1.head < q1.tail && q2.head < q2.tail) {
  // 小哼出一张牌
  t = q1.data[q1.head]
  // 判断小哼当前打出的牌是否能赢牌
  if (book[t] === 0) {  // 表明桌上没有牌面为t的牌
    // 小哼此轮没有赢牌
    q1.head++  // 小哼已经打出一张牌，所以要把打出的牌出队
    s.top++
    s.data[s.top] = t  // 再把打出的牌放到桌上，即入栈
    book[t] = 1 // 标记桌上现在已经有牌面为t的牌
  } else {
    // 小哼此轮可以赢牌
    q1.head++
    q1.data[q1.tail] = t
    q1.tail++
    while (s.data[s.top] !== t) { // 把桌上可以赢得的牌依次放到手中牌的末尾
      book[s.data[s.top]] = 0 // 取消标记
      q1.data[q1.tail] = s.data[s.top] // 依次放入队尾
      q1.tail++
      s.top--  // 栈中少了一张牌，所以栈顶要减1
    }
  }

  // 小哈出一张牌
  t = q2.data[q2.head]
  // 判断小哈当前打出的牌是否能赢牌
  if (book[t] === 0) {  // 表明桌上没有牌面为t的牌
    // 小哈此轮没有赢牌
    q2.head++  // 小哈已经打出一张牌，所以要把打出的牌出队
    s.top++
    s.data[s.top] = t  // 再把打出的牌放到桌上，即入栈
    book[t] = 1 // 标记桌上现在已经有牌面为t的牌
  } else {
    // 小哈此轮可以赢牌
    q2.head++
    q2.data[q2.tail] = t
    q2.tail++
    while (s.data[s.top] !== t) { // 把桌上可以赢得的牌依次放到手中牌的末尾
      book[s.data[s.top]] = 0 // 取消标记
      q2.data[q2.tail] = s.data[s.top] // 依次放入队尾
      q2.tail++
      s.top--  // 栈中少了一张牌，所以栈顶要减1
    }
  }
}

if (q2.head === q2.tail) {
  console.log('小哼赢')
  console.log('小哼当前手中的牌是：')
  for (let i = q1.head; i <= q1.tail-1; i++) {
    console.log(q1.data[i])
  }
  if (s.top > 0) { // 如果桌上有牌则依次输出桌上的牌
    console.log('桌上的牌是：')
    for (let i = 1; i <= s.top; i++) {
      console.log(s.data[i])
    }
  } else {
    console.log('桌上已经没有牌了')
  }
} else {
  console.log('小哈赢')
  console.log('小哈当前手中的牌是：')
  for (let i = q2.head; i <= q2.tail-1; i++) {
    console.log(q2.data[i])
  }
  if (s.top > 0) { // 如果桌上有牌则依次输出桌上的牌
    console.log('桌上的牌是：')
    for (let i = 1; i <= s.top; i++) {
      console.log(s.data[i])
    }
  } else {
    console.log('桌上已经没有牌了')
  }
}

第4节 链表

function Node(element) {
    this.element = element
    this.next = null
    this.prev = null
}

function LinkList() {
    this.head = new Node('head')
    this.tail = new Node('tail')
    this.head.next = this.tail
    this.tail.prev = this.head
}

LinkList.prototype = {
    find: function (item) {
        var currNode = this.head
        while ((currNode !== null) && (currNode.element !== item)) {
            currNode = currNode.next
        }
        return currNode
    },
    findFromTail: function (item) {
        var currNode = this.tail
        while ((currNode !== null) && (currNode.element !== item)) {
            currNode = currNode.prev
        }
        return currNode
    },
    insert: function (newElement, item) {
        var newNode = new Node(newElement)
        var currNode = this.findFromTail(item)
        if (currNode !== null) {
            if (currNode.next === null) {
                currNode.next = newNode
                newNode.prev = currNode
            } else {
                currNode.next.prev = newNode
                newNode.next = currNode.next
                newNode.prev = currNode
                currNode.next = newNode
            }
        } else {
            this.tail.prev.next = newNode
            newNode.prev = this.tail.prev
            newNode.next = this.tail
            this.tail.prev = newNode
        }

    },
    findPrevious: function (item) {
        var currNode = this.head
        while ((currNode.next !== null) && (currNode.next.element !== item)) {
            currNode = currNode.next
        }
        return currNode

    },
    remove: function (item) {
        // var prevNode = this.findPrevious(item)
        // if (prevNode.next !== null) {
        //     prevNode.next = prevNode.next.next
        // }
        var currNode = this.find(item)
        if (currNode.next === null) {
            currNode.prev.next = null
        } else {
            currNode.prev.next = currNode.next
            currNode.next.prev = currNode.prev
        }
    },
    edit: function (item, newElement) {
        var currNode = this.find(item)
        currNode.element = newElement
    },
    display: function () {
        var currNode = this.head
        while (currNode !== null) {
            console.log(currNode.element)
            currNode = currNode.next
        }
    }
}

var nums = new LinkList()
nums.insert('1', 'head')
nums.insert('2', '1')
nums.insert('3', '2')
nums.insert('4', '3')
nums.insert('10', '11')
nums.display()    // head 1 2 3 4 10 tail

第3章 枚举！很暴力

第1节 坑爹的奥数

// XXX + XXX = XXX，将数字1-9分别填入9个X中，每个数字只能使用一次使得等式成立，例如173 + 286 = 459
// 算法逻辑如下：
// num数组表示9个位置的对应的数字
const num = []
num.length = 10

const book = []
book.length = 10

var i , total = 0, sum

for (num[1] = 1; num[1] <= 9; num[1]++) {
    for (num[2] = 1; num[2] <= 9; num[2]++) {
        for (num[3] = 1; num[3] <= 9; num[3]++) {
            for (num[4] = 1; num[4] <= 9; num[4]++) {
                for (num[5] = 1; num[5] <= 9; num[5]++) {
                    for (num[6] = 1; num[6] <= 9; num[6]++) {
                        for (num[7] = 1; num[7] <= 9; num[7]++) {
                            for (num[8] = 1; num[8] <= 9; num[8]++) {
                                for (num[9] = 1; num[9] <= 9; num[9]++) {
                                    // 初始化book数组
                                    for (i = 1; i <= 9; i++) {
                                        book[i] = 0
                                    }
                                    // 如果某个数出现过就标记一下
                                    for (i = 1; i <= 9; i++) {
                                        book[num[i]] = 1
                                    }
                                    // 统计共出现了多少个不同的数
                                    sum = 0
                                    for (i = 1; i <= 9; i++) {
                                        sum += book[i]
                                    }
                                    // 如果正好出现了9个不同的数，~并且满足等式条件，则输出
                                    if (sum === 9 && (num[1] * 100 + num[2] * 10 + num[3] +
                                        num[4] * 100 + num[5] * 10 + num[6] ===
                                        num[7] * 100 + num[8] * 10 + num[9])) {
                                        total++
                                        console.log(num[1] + ',' + num[2] + ',' + num[3] + ',' + num[4] + ',' + num[5] + ',' + num[6] + ',' + num[7] + ',' + num[8] + ',' + num[9])
                                        console.log( '' + num[1] + num[2] + num[3] + '+' + num[4] + num[5] + num[6] + '=' + num[7] + num[8] + num[9])
                                    }
                                }
                            }
                        }
                    }
                }
            }
        }
    }
}

console.log('total:', total / 2)   // 168

第6章 最短路径

第5节 只有五行的算法——Floyd-Warshall

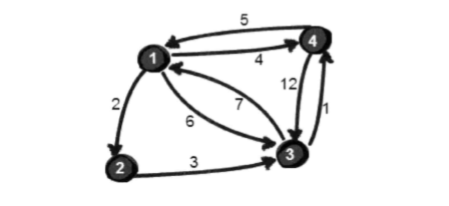
• 上图中有4个城市8条公路，公路上的数字表示这条公路的长短。请注意这些公路是单向的。我们现在需要求任意两个城市之间的最短路程，也就是求任意两个点之间的最短路径。这个问题也被称为“多源最短路径”问题。

// 最短路径--动态规划的思想
// Floyd-Warshall算法是解决任意两点间的最短路径的一种算法。通常可以在任何图中使用，包括有向图、带负权边的图。  算法的时间复杂度为O（N^3）
// 该算法不能解决带有“负权回路”（或者叫“负权环”）的图。因为这类型的图没有最短路径

var k, i, j, t1, t2, t3
var inf = 999999
var n = 4 // 表示4个点
var m = 8 // 表示4个点之间所有边之和
var e = [[], [], [], [], []]

// 初始化--默认点与点之间都有边，且距离为inf（无穷大）
for (i = 1; i <= n ; i++) {
  for (j = 1; j <= n; j++) {
    if (i === j) {
      e[i][j] = 0 // 表示 始点和终点相同的时候，距离为0
    } else {
      e[i][j] = inf // 表示 从i点到j点的距离为inf（无穷大）
    }
  }
}

// 给部分点与点之间设置边以及距离
e[1][2] = 2 // 表示 从1点 到 2点 的距离为 2
e[1][3] = 6 // 表示 从1点 到 3点 的距离为 6
e[1][4] = 4 // 表示 从1点 到 4点 的距离为 4
e[2][3] = 3 // 表示 从2点 到 3点 的距离为 3
e[3][1] = 7 // 表示 从3点 到 1点 的距离为 7
e[3][4] = 1 // 表示 从3点 到 4点 的距离为 1
e[4][1] = 5 // 表示 从4点 到 1点 的距离为 5
e[4][3] = 12 // 表示 从4点 到 3点 的距离为 12

// 最短路径--算法核心语句
for (k = 1; k <= n; k++) {
  for (i = 1; i <= n; i++) {
    for (j = 1; j <= n; j++) {
      if ((e[i][k] < inf) && (e[k][j] < inf) && (e[i][j] > e[i][k] + e[k][j])) {
        e[i][j] = e[i][k] + e[k][j]
      }
    }
  }
}

// 输出结果
for (i = 1; i<= n; i++) {
  for (j = 1; j <= n; j++) {
    console.log('从' + i + '点到' + j + '点的最短距离为' + e[i][j])
    console.log('-----------------------------------------------')
  }
}

第7章 神奇的树

第2节 二叉树

• 二叉树的性质
  • 在二叉树的第i层上最多有2^(i-1)个节点(i>=1)
  • 深度为k的二叉树最多有2^k-1个节点(k>=1)
  • 对任何一棵二叉树T，如果其终端节点数为n0，度为2的节点数为n2，则n0=n2+1
    • 一棵深度为k且有2^k-1个节点的二叉树称为满二叉树
    • 深度为k的，有n个节点的二叉树，当且仅当其每一个节点都与深度为k的满二叉树中编号从1至n的节点一一对应时，称之为完全二叉树
• 二叉树的遍历
  • 二叉树的遍历指的是按照某种顺序，依次访问二叉树的每个节点，有且访问一次
  • 二叉树的遍历有以下三种
    • 前序遍历，从根节点，到左子树，再到右子树，简称根左右
    • 中序遍历，从左节点，到根节点，再到右子树，简称左根右
    • 后序遍历，从左子树，到右子树，再到根节点，简称左右跟
• 完全二叉树的特性
  • 具有n个节点的完全二叉树的深度为Math.floor(log2 n)+1
  • 如果对一棵有n个节点的完全二叉树(其深度为Math.floor(log2 n)+1)的节点按层序编号(从第1层到第Math.floor(log2 n)+1，每层从左到右)，则对任一节点(1<=i<=n)有：
    • 如果i=1，则节点i是二叉树的根，无双亲；如果i>1，则其双亲parent(i)是节点Math.floor(i/2)
    • 如果2i>n，则节点i无左孩子(节点i为叶子节点)；否则其左孩子LChild(i)是节点2i
    • 如果2i+1>n，则节点i无右孩子；否则其右孩子RChild(i)是节点2i+1
• 综上：
  • 完全二叉树：若设二叉树的深度为h，除第h层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层所有的结点都连续集中在最左边，这就是完全二叉树。
  • 满二叉树的任意节点，要么度为0，要么度为2.

// 定义一个节点类
function Node (data, left, right) {
  this.data = data
  this.left = left
  this.right = right
  this.show = function () {
    return this.data
  }
}

// 定义一个二叉查找树类BST
function BST () {
  this.root = null
  this.insert = insert
  this.preOrder = preOrder
  this.inOrder = inOrder
  this.postOrder = postOrder
}

// 插入节点
function insert (data) {
  // 创建一个节点保存数据
  var node = new Node(data, null, null)
  // 下面将节点node插入到树中
  // 如果树是空的，就将节点设为根节点
  if (!this.root) {
    this.root = node
  } else {
    //树不为空
    // 判断插在父节点的左边还是右边
    // 所以先要保存一下父节点
    // var parent = this.root;
    var current = this.root
    var parent
    // 如果要插入的节点键值小于父节点键值，则插在父节点左边，
    // 前提是父节点的左边为空，否则要将父节点往下移一层，
    // 然后再做判断
    while (true) {
      // data小于父节点的键值
      parent = current
      if (data < parent.data) {
        // 将父节点往左下移(插入左边)
        // parent = parent.left;
        current = current.left
        // 如果节点为空，则直接插入
        if (!current) {
          // ！！！此处特别注意，如果就这样把parent赋值为node，也仅仅只是parent指向node，
          // 而并没有加到父元素的左边！！！根本没有加到树中去。所以要先记住父元素，再把当前元素加入进去
          parent.left = node
          break
        }
      } else {
        // 将父节点往右下移(插入右边)
        current = current.right
        if (!current) {
          parent.right = node
          break
        }
      }
    }
  }
}

// 先序遍历(根左右)
function  preOrder (node) {
  if (node) {
    // console.log(node.show())
    DLR_arr.push(node.show())
    if (!node.left && !node.right && DLR_arr.length === 5) {
      console.log("前序遍历：", DLR_arr);
    }
    this.preOrder(node.left)
    this.preOrder(node.right)
  }
}

// 中序遍历(左根右)
function  inOrder (node) {
  if (node) {
    this.inOrder(node.left)
    // console.log(node.show())
    LDR_arr.push(node.show())
    if (!node.left && !node.right && LDR_arr.length === 5) {
      console.log("中序遍历：", LDR_arr);
    }
    this.inOrder(node.right)
  }
}

// 后序遍历(左右根)
function postOrder (node) {
  if (node) {
    this.postOrder(node.left)
    this.postOrder(node.right)
    // console.log(node.show())
    LRD_arr.push(node.show())
    if (LRD_arr.length === 5) {
      console.log("后序遍历：", LRD_arr);
    }
  }
}

// 实例化一个BST树
var tree = new BST()
// 添加节点
tree.insert(30)
tree.insert(14)
tree.insert(35)
tree.insert(12)
tree.insert(17)

var DLR_arr = []
var LDR_arr = []
var LRD_arr = []

// 先序遍历
tree.preOrder(tree.root)
// 中序遍历
tree.inOrder(tree.root)
// 后序遍历
tree.postOrder(tree.root)

第3节 堆——神奇的优先队列

• 一种特殊的二叉树
• 最小堆：所有父节点都比子节点要小
• 最大堆：所有父节点都比子节点要大
• 应用：优先队列：支持插入元素和寻找最大（小）值元素的数据结构

// Base
var h = [0, 99, 5, 36, 7, 22, 17, 46, 12, 2, 19, 25, 28, 1, 92] // 用来存放堆的数组

var n = 14 // 用来存放堆中元素的个数，也就是堆的大小

var sum = n

// 交换函数，用来交换堆中的两个元素的值
function swap (x, y) {
    let t = h[x]
    h[x] = h[y]
    h[y] = t
}

// 向下调整函数
function siftDown (i) {
    let t
    let flag = 0
    while (i * 2 <= n && flag === 0) {
        if (h[i] > h[i * 2]) {
            t = i * 2
        } else {
            t = i
        }
        if (h[t] > h[i * 2 + 1]) {
            t = i * 2 + 1
        }
        if (t !== i) {
            swap(i , t)
            i = t
        } else {
            flag = 1
        }
    }
}

// 建立堆函数
function create () {
    let i
    for (i = Math.floor(n / 2); i >= 1; i--) {
        siftDown(i)
    }
}

// 删除最小元素
function deleteMin () {
    let t
    t = h[1]
    h[1] = h[n]
    n--
    siftDown(1)
    return t
}

create()

for (let j = 1; j <= sum ; j++) {
    console.log(deleteMin())  // 1, 2, 5, 7, 12, 17, 19, 22, 25, 28, 36, 46, 92, 99
}

// More
var h = [0, 99, 5, 36, 7, 22, 17, 46, 12, 2, 19, 25, 28, 1, 92] // 用来存放堆的数组

var n = 14 // 用来存放堆中元素的个数，也就是堆的大小

function HeapSort (h, n ,n) {
    this.h = h
    this.n = n
    this.num = n
}

HeapSort.prototype = {
    swap: function (x, y) {
        let t = this.h[x]
        this.h[x] = this.h[y]
        this.h[y] = t
    },
    siftDown: function (i) {
        let t
        let flag = 0
        while (i * 2 <= this.n && flag === 0) {
            if (this.h[i] > this.h[i * 2]) {
                t = i * 2
            } else {
                t = i
            }
            if (this.h[t] > this.h[i * 2 + 1]) {
                t = i * 2 + 1
            }
            if (t !== i) {
                this.swap(i , t)
                i = t
            } else {
                flag = 1
            }
        }
    },
    create: function () {
        let i
        for (i = Math.floor(this.n / 2); i >= 1; i--) {
            this.siftDown(i)
        }
    },
    deleteMin: function () {
        let t
        t = this.h[1]
        this.h[1] = this.h[this.n]
        this.n--
        this.siftDown(1)
        return t
    }
}

var newHeap = new HeapSort(h, n, n)

newHeap.create()

for (let j = 1; j <= newHeap.num ; j++) {
    console.log(newHeap.deleteMin())  // 1, 2, 5, 7, 12, 17, 19, 22, 25, 28, 36, 46, 92, 99
} 

第4节 擒贼先擒王——并查集

// 存放每个节点的根节点
var f = []

// 记录节点的个数
var n = 10

// 有关联的节点关系
var m = []
m.length = 10
m[1] = [1, 2]
m[2] = [3, 4]
m[3] = [5, 2]
m[4] = [4, 6]
m[5] = [2, 6]
m[6] = [8, 7]
m[7] = [9, 7]
m[8] = [1, 6]
m[9] = [2, 4]

// 记录独立根节点的个数
var sum = 0

// 初始化 数组里 存的是 自己数组下标的编号
function init () {
  for (let i = 1; i <= n; i++) {
    f[i] = i
  }
}

// 找祖宗的递归函数，不停地去找祖宗，直到找到祖宗为止，
// 其实就是去找犯罪团伙的最高领导人，“擒贼先擒王”原则
function getF (v) {
  if (f[v] === v) {
    return v
  } else {
    // 这里是路径压缩，每次在函数返回的时候，顺带把路上遇到的人的“BOSS”改为最后
    // 找到的祖宗编号，也就是犯罪团伙的最高领导人编号。这样可以提高今后找到犯罪团伙的最高领导人
    //（其实就是树的祖先）的速度
    f[v] = getF(f[v])
    return f[v]
  }
}
// 合并两子集合的函数
function merge (v, u) {
  let t1, t2
  t1 = getF(v)
  t2 = getF(u)
  if (t1 !== t2) {  // 判断两个节点是否在同一个集合中，即是否为同一个祖先
    f[t2] = t1
    // “靠左”原则左边变成右边的BOSS。即把右边的集合，作为左边集合的子集合。
    // 经过路径压缩后，将f[u]的根的值也赋值为v的祖先f[t1]
  }
}

// 初始化
init()
// 开始合并犯罪团伙
for (let i = 1; i < m.length; i++) {
  merge(m[i][0], m[i][1])
}
// 求出独立的根节点,即扫描出有多少个独立的犯罪团伙
for (let i = 1; i <= n; i++) {
  if (f[i] === i) {
    sum++
  }
}

console.log(sum)  // 3