基于正态分布的前端性能数据分析（一）公司的前端项目是上报了各项性能数据的，如首屏时间、onload时间、网络用时等；由于

前言

公司的前端项目是上报了各项性能数据的，如首屏时间、onload时间、网络用时等；由于用户可能处于各类环境中，如不同的网络环境、机型差异、同一手机的不同运行状态等，导致性能数据会有较大的波动，而这些异常数据对平均值的影响是非常大的，因此不能简单地用平均值描述性能状况，而应该做更加深入地分析数据。

通过对性能数据的统计分析，我们希望得到性能数据的分布情况，监控上线前后的性能变化，甚至运行期间的性能波动，分析原因出在哪个环节，从而有针对性地优化项目；并且针对每一次优化，我们能够定量地确定优化成效有多大，而不是“嗯，好像优化有效果，在我的电脑上都变快了”

ps：由于不是专业做数据分析的，分析过程如果有不合理的地方，欢迎指正。

探索

由于我们主要关注用户的首屏时间，因此我这里拿到了一周内首屏数据的抽样结果（约13万条），为了了解首屏时间的分布情况，我以50ms为间距统计各个时间段内的数据量，绘制折线图结果如下：

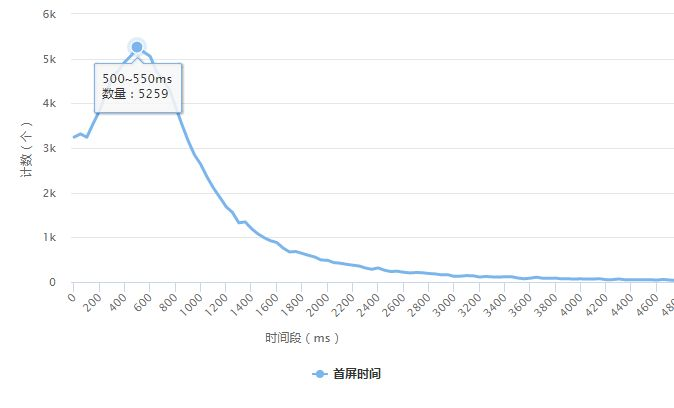
可以看到数据分布比较对称，曲线呈钟形，数据主要集中在550ms附近。

在传统的统计分析当中，很多时候我们都希望用正态分布来分析数据，就算不符合正态分布的数据，也有可能将原始数据转换为正态数据。

从上图可以看到，我们的数据是比较符合正态分布的特征的，因此我们可以尝试使用正态分布来分析。

这里简单回顾一下正态分布（也就是高中数学内容）：

若随机变量 X服从一个位置参数为 $\mu$ 、尺度参数为的 $\sigma$ 的概率分布，且其概率密度函数为

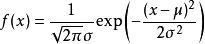
则这个随机变量就称为正态随机变量，正态随机变量服从的分布就称为正态分布，记作N( $\mu$ , $\sigma^{2}$ )。如果 $\mu=0$ ， $\sigma=1$ ，称作标准正态分布。其概率分布图如下：

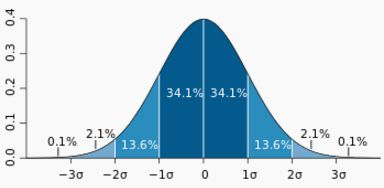
生活中，比如考试分数、身高、收入、智商等都符合正态分布或近似正态分布，也就是数据主要集中在一个范围，向两边逐渐减少的分布趋势。（ps：所以不要气馁于自己的平凡，因为平凡人才是大多数，哈哈）。

在做正态分析之前，需要做正态性检验，也就是检验我们的数据与正态分布的相似程度，如果差得太远，就需要做转换或者改用其他分析方式。

验证

我们可以使用IBM的数据分析工具SPSS来验证数据是否符合正态分布，对于大样本数据，SPSS使用的是K-S检验，其中K（Kurtosis）指峰度、S（Skewness）指偏度；并且SPSS会给出数据的直方图、Q-Q图，从而直观地反应数据的正态性。这些数据SPSS都会帮我们算好，因此我们可以暂时不用深究，会用这些数据就行。

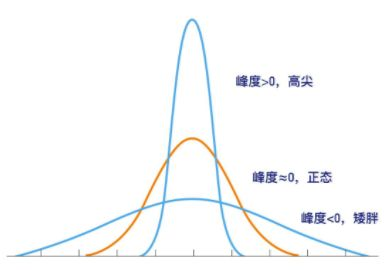
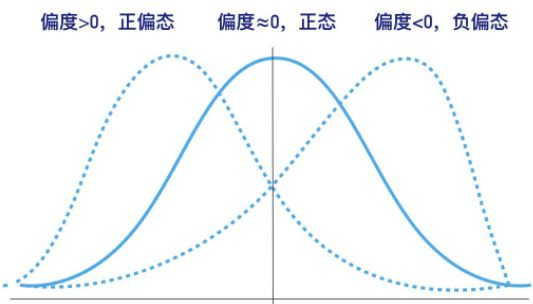
峰度：可以理解为曲线的陡峭程度，正态分布的峰度为3，峰度越接近3，说明曲线的正态性越好，通常峰度大于峰度标准误差的1.96倍，即可认为数据不符合正态分布。SPSS已经把正态分布的峰度转换成了0，以方便比较，因此在SPSS中峰度越接近0，正态性越好。
偏度：描述数据的对称性，也就是偏离正态分布中心的程度。正态分布的偏度为0，偏度越接近0，说明数据正态性越好；同样，通常偏度大于偏度标准误差的1.96倍，即可认为数据不符合正态分布。
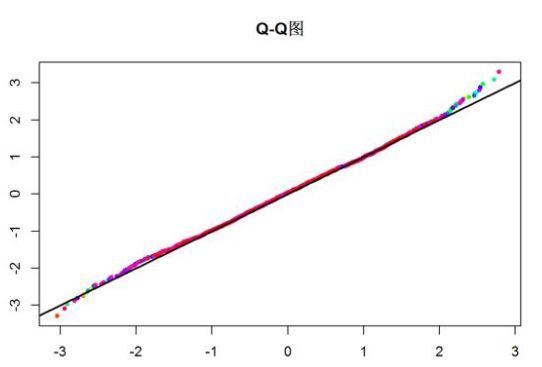
Q-Q图：如果Q-Q图中的散点数据主要分布于一条直线上，则可认为数据具有正态性。

图源1、图源2

在开始处理之前，我们还需要舍去原始数据中的异常数据；比如首屏时间10s以上、100ms以下的显然不合理，进一步观察发现，3000ms以上的各个时间段内的数据量都比较小，再结合项目实际情况，判断3000ms是一个比较合理的异常界线，故舍去大于3000ms的数据（舍去数据量小于10%）。

接下来将过滤后的数据导入SPSS进行验证，在SPSS中依次选择 分析->描述统计->探索，并在绘制选项中选择 正态检验 和 直方图，结果如下：

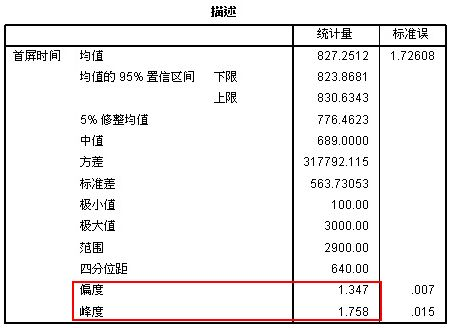
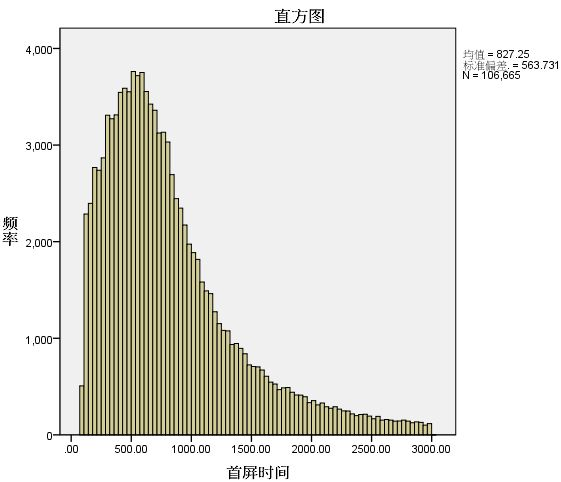
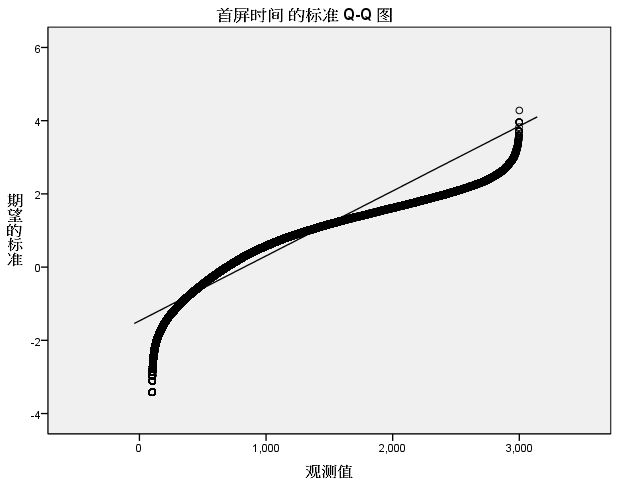
可以看到，峰度和偏度大于1，直方图程正偏态，Q-Q图也不在一条直线上。因此我们的原始数据正态性并不是很好，需要转换数据后再做验证。

数据转换

要将数据转换为正态分布，通常可以计算原始数据的SQRT（开方）、LN（自然对数）、LG（10为底的对数）、倒数，它们的转换力度依次增大；对于正偏态数据，可以直接转换，而负偏态数据需要先求出数据的最大值（max），然后对于每一项数据（x），以求LN为例，计算方式为 LN(max+1-x)。

可以多次交替、循环使用上述的转换方式，以达到更好的转换效果。

多次尝试过后，我采用了对原始数据开方三次的方式，也就是取1/8次方。将处理后的数据导入SPSS，分析结果如下：

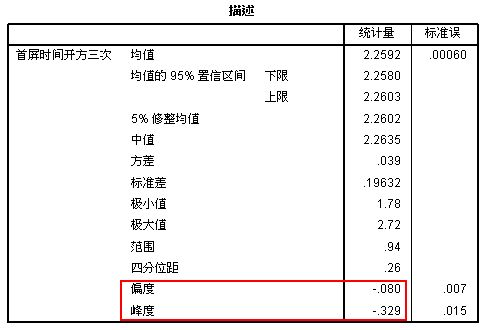
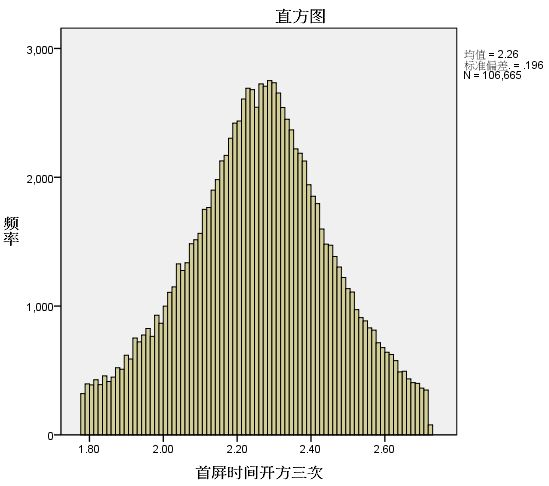
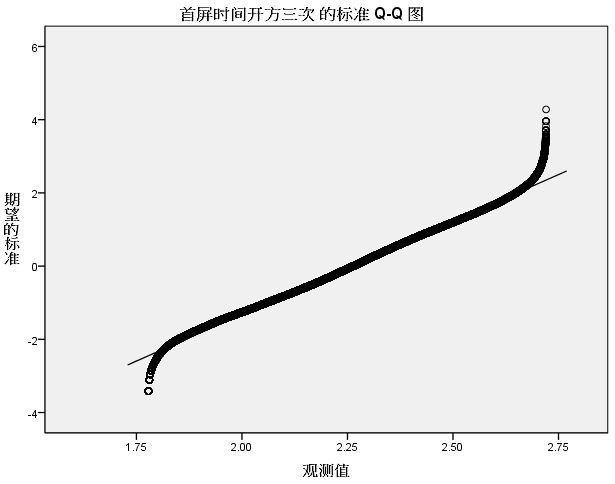
可以看到，相较于未转换的数据，正态性已经好了很多，峰度、偏度已经接近0，直方图比较对称，Q-Q图的大部分已经在一条直线上了。

需要指出的是，在传统的统计分析中，30个样本以上就算是大样本了，传统的正态检验方法并不适应于验证超大样本数据（如我这里有10万条数据），并且由于正态性检验较为敏感，因此我们可以不做严格的显著性检验，也就是不强制要求上述的 1.96倍标准，只是将峰度、偏度作为参考，越接近0越好，然后辅以直方图、Q-Q图的佐证。

另外根据中心极限定理，在样本容量很大时，总体参数的抽样分布是趋向于正态分布的，因此我们是可以使用正态分布来分析我们的数据的，当然，为了更好的效果，我们最好对原始数据进行转换。

这一篇文章，主要介绍了正态分布的概念、对原始数据的转换方式以及如何验证数据的正态性，下一篇文章将会使用正态分布来分析数据。