上一篇文章已经验证了，可以使用正态分布来分析我们的首屏时间（需转换为其值的1/8次方），接下来就进入分析部分。
计算首屏时间的正态函数
根据正态分布的概率密度函数：
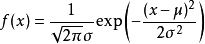
要描述一个正态分布，只需要知道其平均值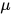（ ）和标准差（
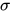）就行了，记作
。
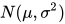首先将过滤后的数据开方三次（1/8次方），计算开方后数据的平均值为2.259，标准差为0.19632，也就是转换后的数据符合正态分布 。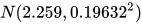
计算首屏时间的分布
对于任一正态总体 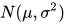，取值小于
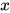的概率为
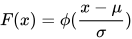
以上面得到的正态分布 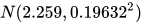为例，求首屏时间小于1000ms的概率，首先计算1000的1/8次方为2.37137，带入公式
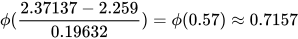
其中 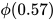的值通过查标准正态分布表得到。也就是说，首屏时间在1000ms以下的用户约占71.57%。
根据上述计算方式，统计首屏时间在各个时间段内的概率，并比较实际数据与转换前后的数据，结果如下：
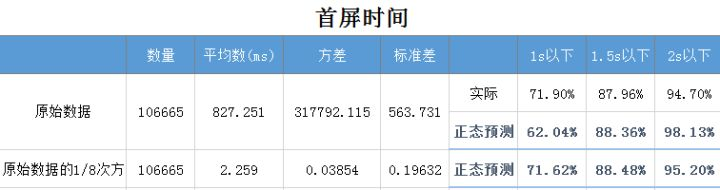
通过与实际数据对比，可以看到，未做数据转换时，对1s以下、2s以下用户占比的预测相对误差较大，而转换后的预测结果已经与实际数据非常接近了。
因为数据是在项目稳定运行期的一周内随机抽样得到的，比较有代表性，从而可以将这些数据作为样本（去除异常值后约10.5万条）推测总体（千万级）数据的首屏时间具有如下特征：
首屏时间的1/8次方满足正态分布 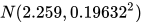，均值为827.251ms，标准差为563.731，分段占比分别为：1s以下71.62%，1.5秒以下88.48%，2秒以下95.20%。
并且我们可以将该正态分布作为基线用于衡量某一天的首屏时间是否有明显波动。
参数检验
上面已经得到了首屏时间的正态分布，当某次项目版本升级，我们如何知道上线前后的性能变化呢？或者我们想了解项目运行期间的性能波动情况，要怎么得到这些信息呢？答案就是参数检验。当总体分布已知时，可以使用参数检验判断两个样本之间的差异性。也就是，我们可以将某一天的数据与上面得到的基线做比较，判断两者是否有差异，有差异就说明有性能变化。
参数检验的过程可以简单地理解为，我们假设上线后性能没有差异，然后计算我们把这个假设拒绝掉，并且还拒绝错了的概率，记作P，也就是说，P越小，越能说明我们没有拒绝错，因此我们应该拒绝原假设，也就是上线前后性能有差异。可能有点绕，不过只需要记住，P越小，差异性越显著。
参数检验的方法有很多种，这里使用Z检验（也叫U检验），计算公式为：
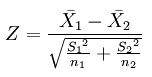
其中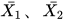， 是样本1、样本2的平均数，
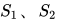是样本1、样本2的标准差，
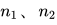为样本1、样本2的样本数量。
计算出的Z的绝对值和P值的关系如下：
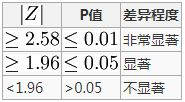
越大P值越小，当计算出的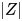
大于2.58时，P值小于0.01，两个样本差异非常显著。
我这里取某一天的首屏数据，同样的，去除异常值，开方三次，再计算平均值和方差，并结合基线正态分布计算Z值：
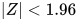，说明这一天的数据与基线差异性不明显，可以认为没有性能波动。
性能波动原因分析
如果有性能波动，该如何分析原因出在哪个部分呢？
首屏时间主要由网络耗时、前端耗时组成，但由于现代浏览器基本都是一边加载资源一边解析，所以首屏时间应该小于两者之和；网络耗时又可以简单分为DNS查询、TCP连接建立、加载资源等时间；前端耗时也就是DOM树构建，渲染树构建以及JS的执行，不过需要注意三者之间的阻塞关系。如果出现性能变化，只需要分析是哪部分变化导致的就行了。
同样，和统计首屏时间类似，也可以统计组成首屏时间的各个部分，不过，我们可能并不需要了解各个部分的具体分布，在去除异常值后，只需要简单地求均值以及方差就行了。首先计算样本数据中各个部分的均值、方差，当出现性能波动时，只需将波动数据与样本数据对应部分的均值、方差做简单的对比，基本就能找出具体是哪个部分波动较大了。
如果确实需要对首屏时间的各个组成部分做分析，和分析首屏时间的方式类似，如果能够转换成正态分布，就按照正态分布分析；对于不能转换成正态分布的部分，可以使用非参数检验（如秩和检验）判断数据之间的差异性。
另外，舍去的异常数据占比也可以作为一个参考值，比如上述的样本数据中异常值占8%左右，如果某次数据中异常值占比偏离这个值太多，也属于非正常情况。
总结
实际应用中，过程大概可以总结为：
- 统计项目稳定期一段时间内的数据，根据实际情况去除异常值
- 转换数据使其贴近正态分布，确定转换后数据所服从的正态分布函数
- 根据正态分布函数可以得到数据的分布情况
- 使用Z检验判断每天的数据与基线数据的差异性，监控性能变化
- 具体分析有显著差异的数据发生变化的原因
