一棵树,如图:
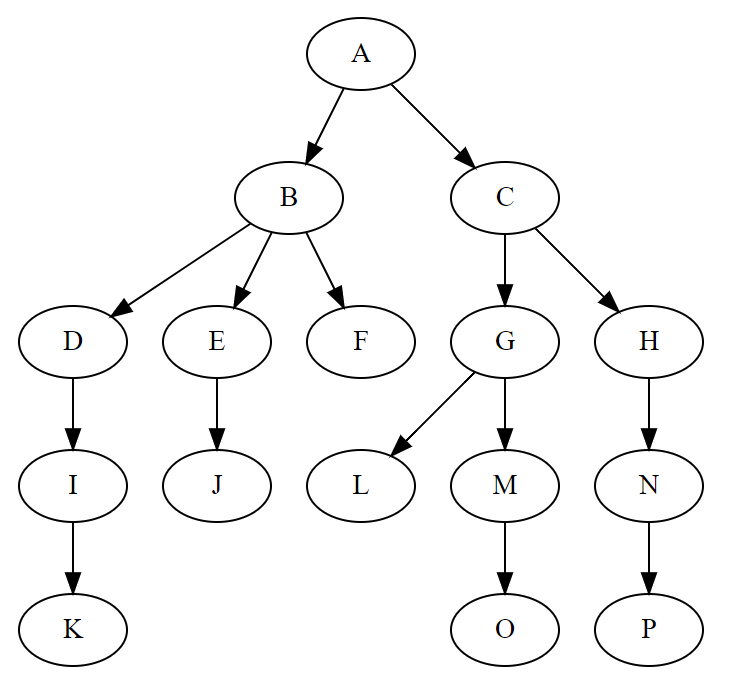
用来模拟具有树状结构性质的数据集合。
它是由n(n>0)个有限节点组成一个具有层次关系的集合。
特点:
每个节点有零个或多个子节点;
没有父节点的节点称为根节点;(A)
每一个非根节点有且只有一个父节点;
除了根节点外,每个子节点可以分为多个不相交的子树;
术语:
节点的度:一个节点含有的子树的个数称为该节点的度;(A的度为2)
树的度:一棵树中,最大的节点的度称为树的度;(树的度=B的度=3)
叶节点或终端节点:度为零的节点;(K、J、F、L、O、P、)
非终端节点或分支节点:度不为零的节点;(B、C、D、E、I、G、H、M、N)
父亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;(A为B的父节点)
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;(B为A的子节点)
兄弟节点:具有相同父节点的节点互称为兄弟节点;(B与C为兄弟节点)
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
深度:对于任意节点n,n的深度为从根到n的唯一路径长,根的深度为0;(K的深度为4)
高度:对于任意节点n,n的高度为从n到一片树叶的最长路径长,所有树叶的高度为0;(B的高度为3)
堂兄弟节点:父节点在同一层的节点互为堂兄弟;(E与G为堂兄弟节点)
节点的祖先:从根到该节点所经分支上的所有节点;(F的祖先为A、B)
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。(D的子孙为I、K)
森林:由m(m>=0)棵互不相交的树的集合称为森林;
树的种类
无序树:树中任意节点的子节点之间没有顺序关系,这种树称为无序树,也称为自由树;
有序树:树中任意节点的子节点之间有顺序关系,这种树称为有序树;
二叉树:二叉树的每个结点至多只有二棵子树(不存在度大于2的结点),二叉树的子树有左右之分,次序不能颠倒。二叉
树的第i层至多有2i-1个结点;深度为k的二叉树至多有2k-1个结点;对任何一棵二叉树T,如果其终端结点数为n0,度为
2的结点数为n2,则n0=n2+1。下图是一个二叉树
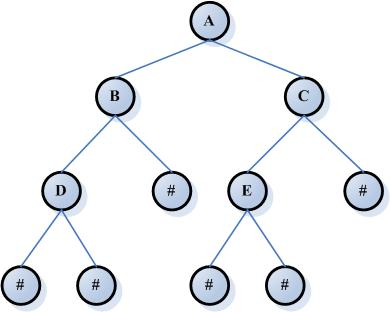
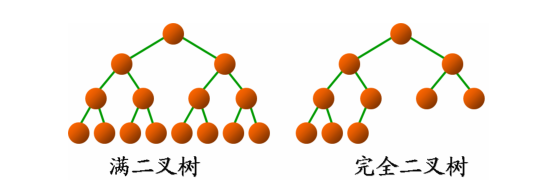
完全二叉树:对于一颗二叉树,假设其深度为d(d>1)。除了第d层外,其它各层的节点数目均已达最大值,且第d层
所有节点从左向右连续地紧密排列,这样的二叉树被称为完全二叉树;
满二叉树:所有叶节点都在最底层的完全二叉树;
平衡二叉树(AVL树):当且仅当任何节点的两棵子树的高度差不大于1的二叉树;
AVL树:解决了二叉查找树退化成链表的问题,把插入,查找,删除的时间复杂度最好情况和最坏情况都维持在O(logN)。
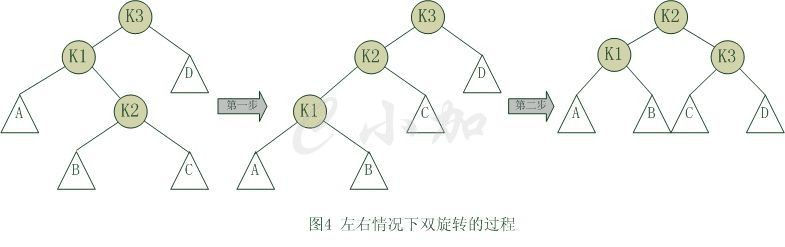
自平衡操作--旋转
单旋转
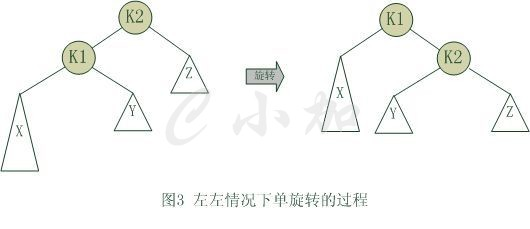
双旋转
红黑树
红黑树是每个节点都带有颜色属性的二叉查找树,颜色为红色或黑色。在二叉查找树强制的一般要求以外,对于
任何有效的红黑树我们增加了如下的额外要求:
性质1. 节点是红色或黑色。
性质2. 根是黑色。
性质3. 所有叶子都是黑色(叶子是NIL节点)。
性质4. 每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点。)
性质5. 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。

排序二叉树(二叉查找树(英语:Binary Search Tree)):也称二叉搜索树、有序二叉树;
霍夫曼树:带权路径最短的二叉树称为哈夫曼树或最优二叉树;
B树:一种对读写操作进行优化的自平衡的二叉查找树,能够保持数据有序,拥有多于两个子树。
B+树
B*树
Tire树称为字典树
以上是对树的一个大体认识,稍后会对每一个树做具体的说明,以及他们在Java中的具体实现,和源码分析。