由散列表到BitMap的概念与应用（二）在前一篇文章中我们介绍了散列表和BitMap的相关概念与部分应用。本文将会具体讲

在前一篇文章中我们介绍了散列表和BitMap的相关概念与部分应用。本文将会具体讲解BitMap的扩展：布隆过滤器（Bloom filter）。

概念

Hash表实际上为每一个可能出现的数字提供了一个一一映射的关系，每个元素都相当于有了自己的独享的一份空间，这个映射由散列函数来提供。Hash表甚至还能记录每个元素出现的次数，利用这一点可以实现更复杂的功能。我们的需求是集合中每个元素有一个独享的空间并且能找到一个到这个空间的映射方法。独享的空间对于我们的问题来说，一个Boolean就够了，或者说，1个bit就够了，我们只想知道某个元素出现过没有。如果为每个所有可能的值分配1个bit，这就是BitMap所要完成的工作。然而当数据量大到一定程度，所需要的存储空间将会超出可承受的范围，如写64bit类型的数据，需要大概2EB存储。

布隆过滤器（Bloom Filter）是1970年由布隆提出的。布隆过滤器可以用于检索一个元素是否在一个集合中。布隆过滤器是一种空间效率极高的概率型算法和数据结构，它实际上是一个很长的二进制向量和一系列随机映射函数。BitMap对于每一个可能的整型值，通过直接寻址的方式进行映射，相当于使用了一个哈希函数，而布隆过滤器就是引入了k(k>1)个相互独立的哈希函数，保证在给定的空间、误判率下，完成元素判重的过程。

算法描述

集合表示与元素查询

具体来看Bloom Filter是如何用位数组表示集合的。初始状态时，Bloom Filter是一个包含m位的位数组，每一位都置为0。

Bloom Filter使用k个相互独立的哈希函数（Hash Function），它们分别将集合中的每个元素映射到{1,…,m}的范围中。对任意一个元素x，第i个哈希函数映射的位置hash_i(x)就会被置为1（1≤i≤k）。

当一个元素被加入集合中时，通过k各散列函数将这个元素映射成一个位数组中的k个点，并将这k个点全部置为1。下图是k=3时的布隆过滤器。

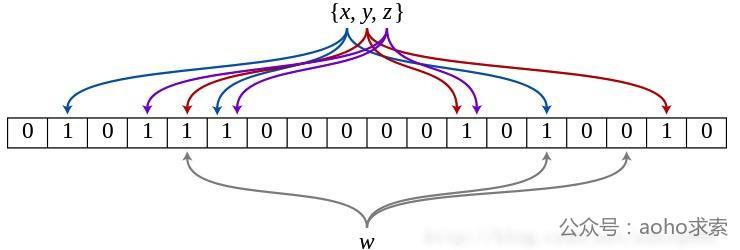
x、y、z经由哈希函数映射将各自在Bitmap中的3个位置置为1，当w出现时，仅当3个标志位都为1时，才表示w在集合中。图中所示的情况，布隆过滤器将判定w不在集合中。

错误率

Bloom Filter有一定的误判率。在判断一个元素是否属于某个集合时，有可能会把不属于这个集合的元素误判为属于这个集合。因此，它不适合那些"零误判"的应用场合。在能容忍低误判的应用场景下，布隆过滤器通过极少的误判换区了存储空间的极大节省。

那么布隆过滤器的误差有多少？我们假设所有哈希函数散列足够均匀，散列后落到Bitmap每个位置的概率均等。Bitmap的大小为m、原始数集大小为n、哈希函数个数为k：

k个相互独立的散列函数，接收一个元素时Bitmap中某一位置为0的概率为：

假设原始集合中，所有元素都不相等（最严格的情况），将所有元素都输入布隆过滤器，此时某一位置仍为0的概率为：

某一位置为1的概率为：

当我们对某个元素进行判重时，误判即这个元素对应的k个标志位不全为1，但所有k个标志位都被置为1，误判率ε约为：

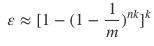
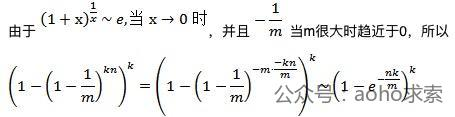
场景

布隆过滤器的最大的用处就是，能够迅速判断一个元素是否在一个集合中。因此他有如下三个使用场景:

网页爬虫对URL的去重，避免爬取相同的URL地址
反垃圾邮件，从数十亿个垃圾邮件列表中判断某邮箱是否垃圾邮箱（同理，垃圾短信）
缓存击穿，将已存在的缓存放到布隆过滤器中，当黑客访问不存在的缓存时迅速返回避免缓存及DB挂掉。

缓存系统中，按照KEY去查询VALUE,当KEY对应的VALUE一定不存在的时候并对KEY并发请求量很大的时候，就会对后端造成很大的压力。如果缓存集中在一段时间内失效，发生大量的缓存穿透，所有的查询都落在数据库上，造成了缓存雪崩。

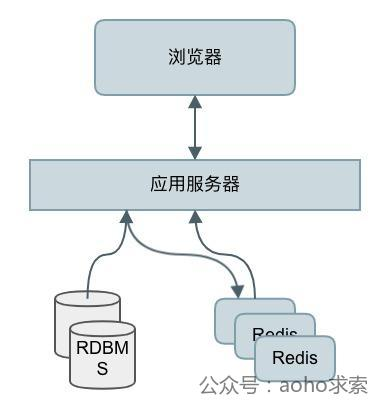
由于缓存不命中，每次都要查询持久层。从而失去缓存的意义。
这里只要增加一个bloom算法的服务，服务端插入一个key时，在这个服务中设置一次。需要查询服务端时，先判断key在后端是否存在，这样就能避免服务端的压力。

实现与应用

下面我们介绍使用Google实现的BloomFilter。

引入依赖

        <dependency>
            <groupId>com.google.guava</groupId>  
            <artifactId>guava</artifactId>  
        </dependency>

查找某个元素

  private static int size = 1000000;

  private static BloomFilter<Integer> bloomFilter =
      BloomFilter.create(Funnels.integerFunnel(), size);

  @Test
  public void consumeTest() {
    for (int i = 0; i < size; i++) {
      bloomFilter.put(i);
    }
    long startTime = System.nanoTime(); // 获取开始时间

    // 判断这一百万个数中是否包含29999这个数

    if (bloomFilter.mightContain(29999)) {
      System.out.println("命中了");
    }
    long endTime = System.nanoTime(); // 获取结束时间
    System.out.println("程序运行时间： " + (endTime - startTime) + "纳秒");
  }

使用BloomFilter查找一个元素29999，非常快速。

误判率

  private static int size = 1000000;

  private static BloomFilter<Integer> bloomFilter =
      BloomFilter.create(Funnels.integerFunnel(), size);

  @Test
  public void errorTest() {

    for (int i = 0; i < size; i++) {
      bloomFilter.put(i);
    }

    List<Integer> list = new ArrayList<>(1000);
    // 取10000个不在过滤器里的值，看看有多少个会被认为在过滤器里
    for (int i = size + 10000; i < size + 20000; i++) {
      if (bloomFilter.mightContain(i)) {
        list.add(i);
      }
    }
    System.out.println("误判的数量：" + list.size());
  }

上述代码所示，我们取10000个不在过滤器里的值，却还有330个被认为在过滤器里，这说明了误判率为0.03。即，在不做任何设置的情况下，默认的误判率为0.03。 BloomFilter默认的构造函数如下：

    @CheckReturnValue
    public static <T> BloomFilter<T> create(Funnel<? super T> funnel, long expectedInsertions) {
        return create(funnel, expectedInsertions, 0.03D);
    }

当然我们可以通过如下的构造函数，手动设置误判率。

private static BloomFilter<Integer> bloomFilter = BloomFilter.create(Funnels.integerFunnel(), size,0.01);

实际应用

  static int sizeOfNumberSet = Integer.MAX_VALUE >> 4;

  static Random generator = new Random();

  @Test
  public void actualTest() {
    int error = 0;
    HashSet<Integer> hashSet = new HashSet<Integer>();
    BloomFilter<Integer> filter = BloomFilter.create(Funnels.integerFunnel(), sizeOfNumberSet);
    System.out.println(sizeOfNumberSet);
    for (int i = 0; i < sizeOfNumberSet; i++) {
      int number = generator.nextInt();
      if (filter.mightContain(number) != hashSet.contains(number)) {
        error++;
      }
      filter.put(number);
      hashSet.add(number);
    }

    System.out.println(
        "Error count: "
            + error
            + ", error rate = "
            + String.format("%f", (float) error / (float) sizeOfNumberSet));
  }

BloomFilter实际的应用类似如上所示，换成redis客户端调用即可，用于redis缓存击穿等场景。

总结

本文主要讲了布隆过滤器相关概念、算法描述、错误率统计和布隆过滤器的实现与应用。布隆过滤器是BitMap的一种工业实现，解决了使用BitMap时当数据量大到一定程度，所需要的存储空间将会超出可承受的范围的问题。

布隆过滤器就是引入了k(k>1)个相互独立的哈希函数，保证在给定的空间、误判率下，完成元素判重的过程。布隆过滤器有一个误判率的概念，误判率越低，则数组越长，所占空间越大。误判率越高则数组越小，所占的空间越小。最后，我们通过Google实现的BloomFilter，介绍如何使用布隆过滤器并自定义调整误判率。

相比于其它的数据结构，布隆过滤器在空间和时间方面都有巨大的优势。布隆过滤器存储空间和插入/查询时间都是常数（O(k)）。哈希表也能用于判断元素是否在集合中，但是布隆过滤器只需要哈希表的1/8或1/4的空间复杂度就能完成同样的问题。

布隆过滤器的缺点除了误算率之外（随着存入的元素数量增加，误算率随之增加。但是如果元素数量太少，则使用散列表足矣），不能从布隆过滤器中删除元素。我们很容易想到把位数组变成整数数组，每插入一个元素相应的计数器加1, 这样删除元素时将计数器减掉就可以了。然而要保证安全地删除元素并非如此简单。首先我们必须保证删除的元素的确在布隆过滤器里面。这一点单凭这个过滤器是无法保证的。

最后，欢迎购买笔者的新书《Spring Cloud微服务架构进阶》。

由散列表到BitMap的概念与应用（二）

概念