目的

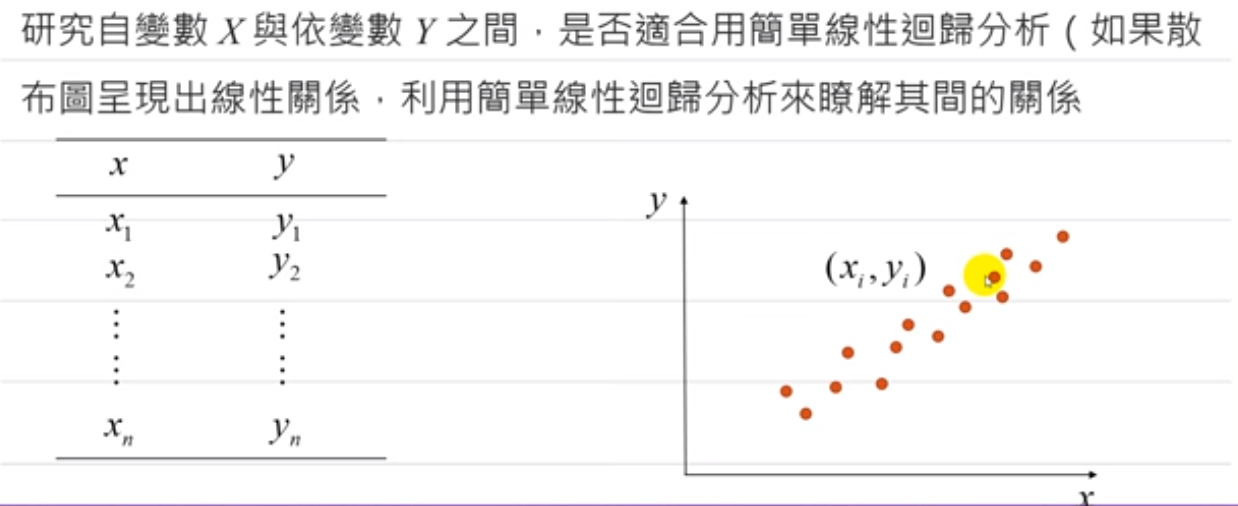
散布图及建立回归模型
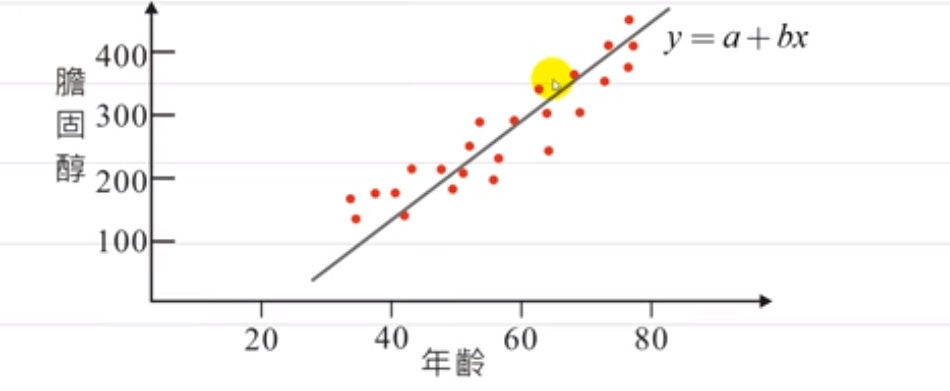
直线统计模型

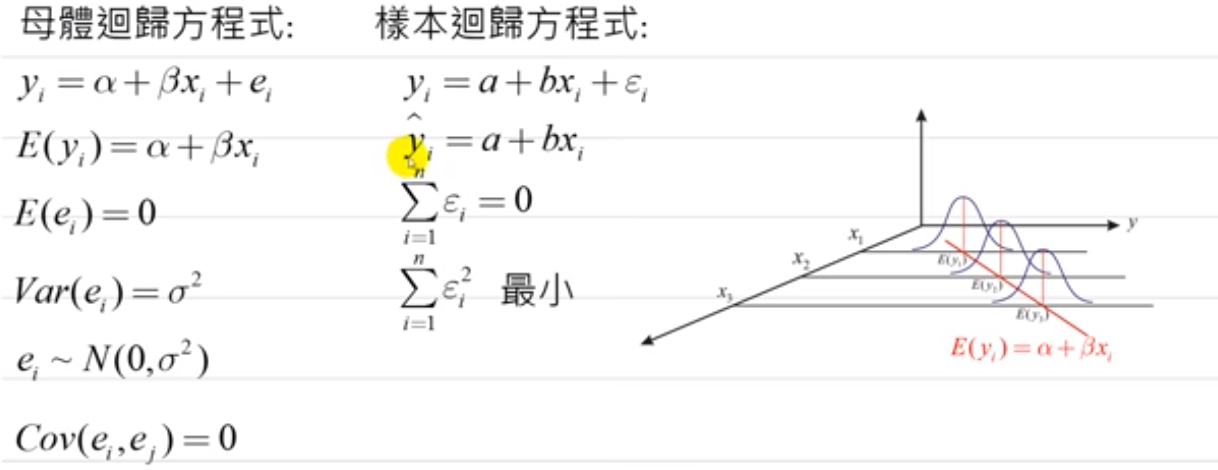
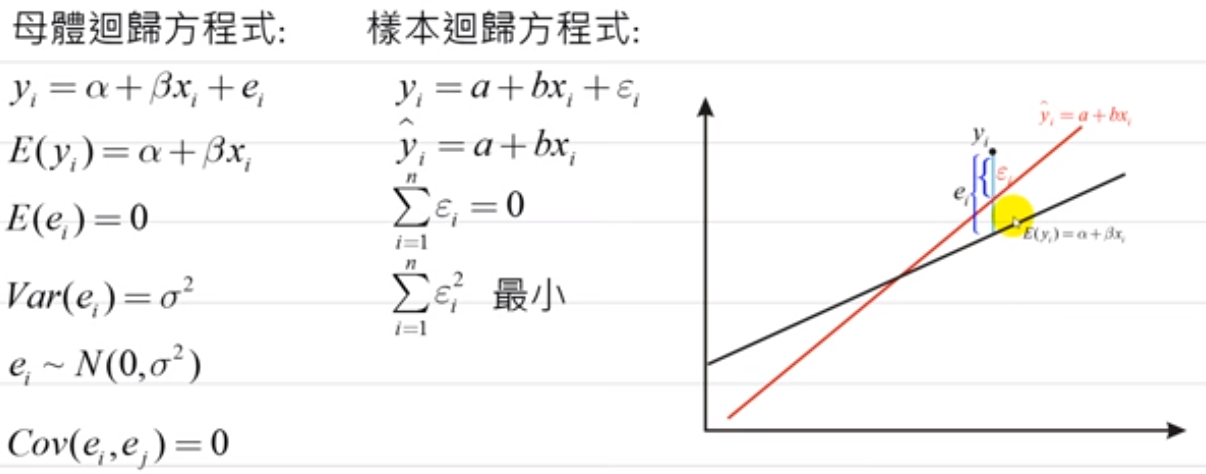
基本假设
散布图(SCATTER DIAGRAM)
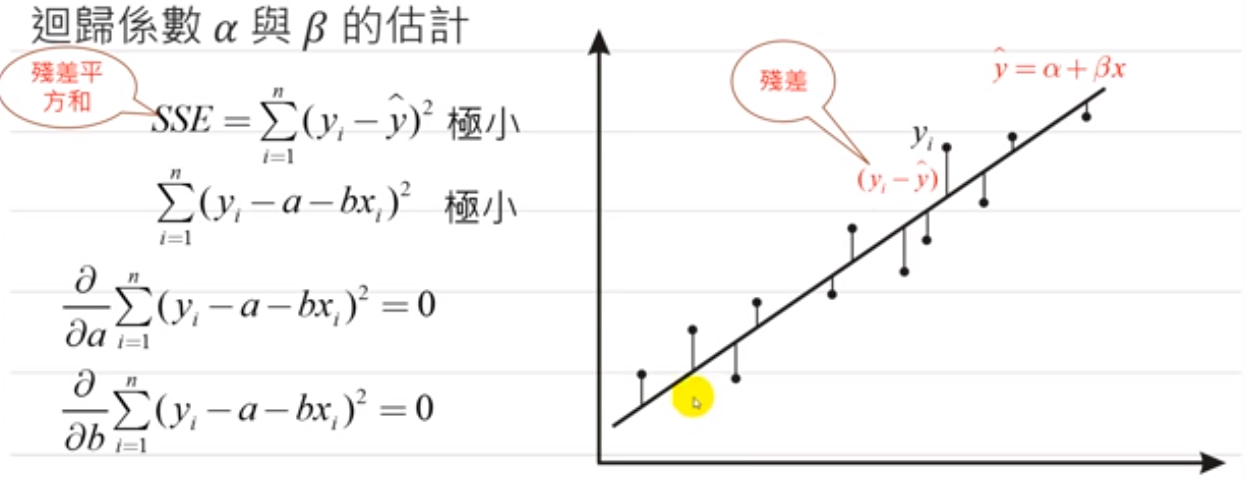
回归分析的目的:
建立方程式(模型),对已知自变量可以预估因变量
若因变量y仅受到自变量x的影响,不受其他因素的影响,称为确定模式(数学函数)
回归模型往往不只是受其他因素的影响。
数学模式就是当已知一个自变量的时候,因变量就确定了,一分一毫都不差。
在回归模型里面已知自变量后,因变量也只是一个大概的范围,不是一个真实的值,而是一个估计值。
最小平方法(OLS)
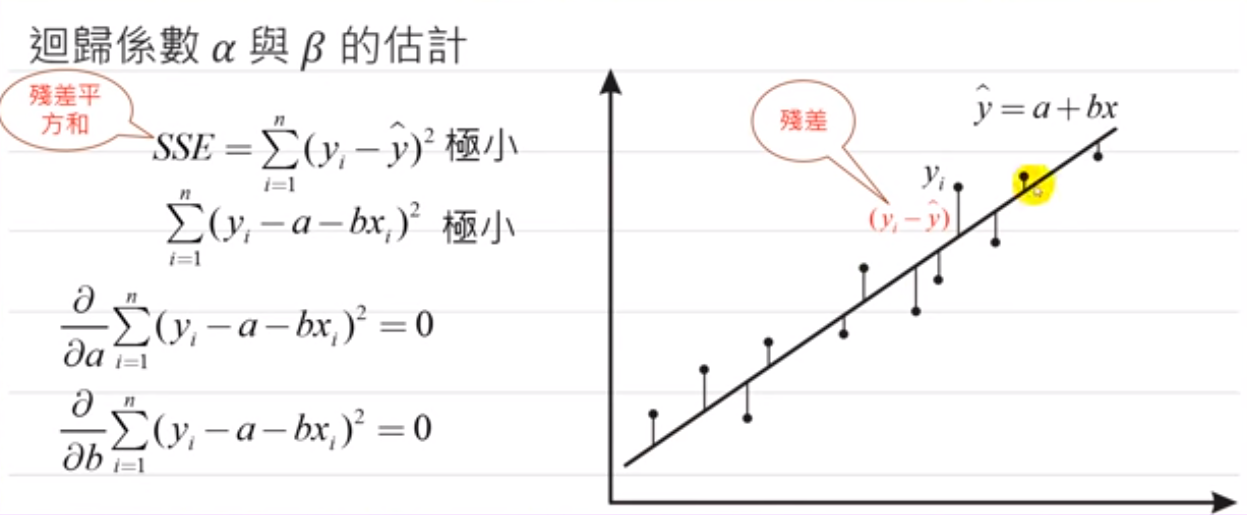
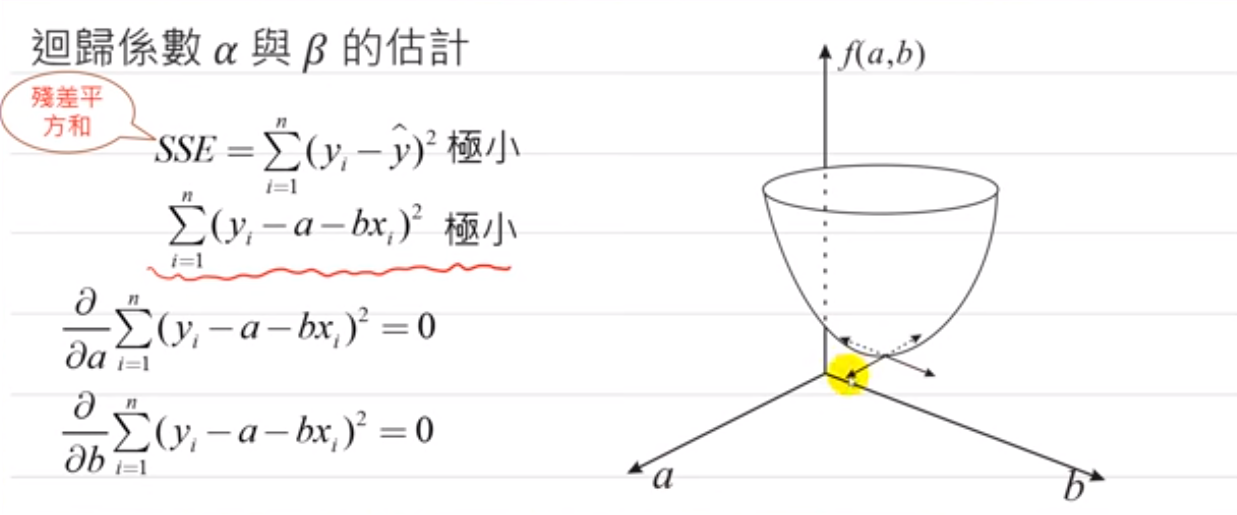
标准方程式(NORMAL EQUATIONS)
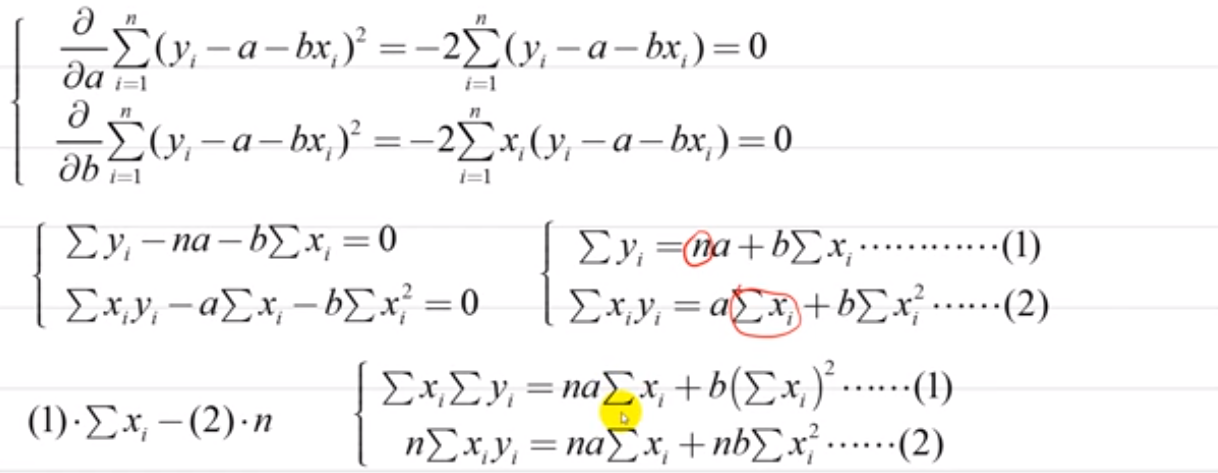

符号记忆公式

回归方程式的例子1

回归方程式的例子2
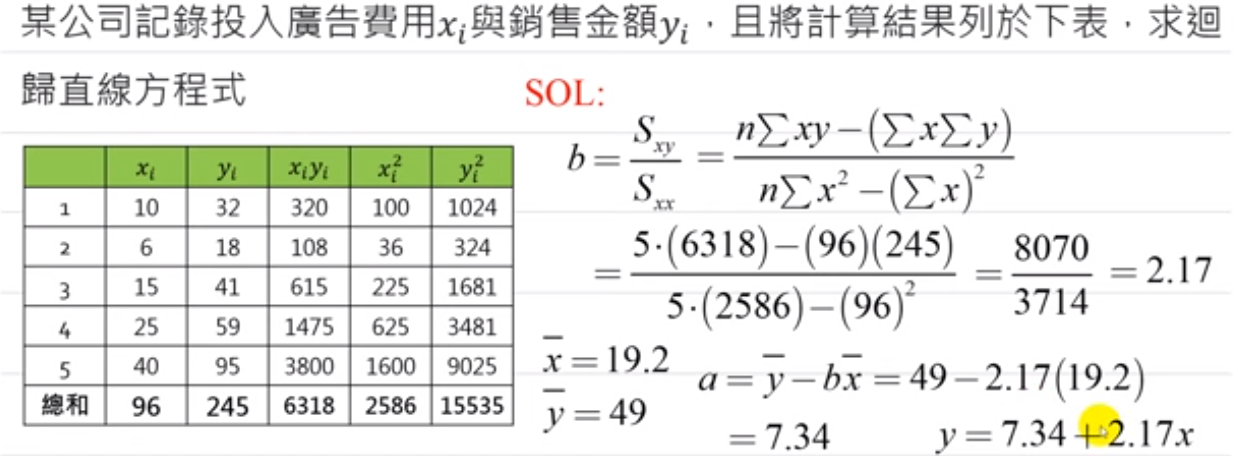
内容归纳
回归方程式的建立技巧
利用最小平方法得到
最小平方法依据
- 残差总和为0
- 残差平方总和最小
- 残差与变数共变数为0
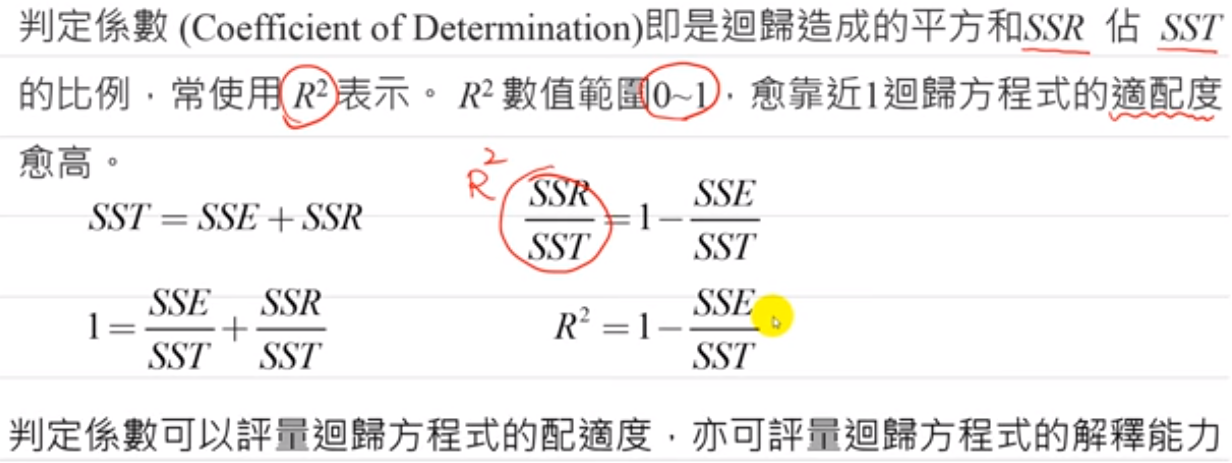
回归模型之适合度
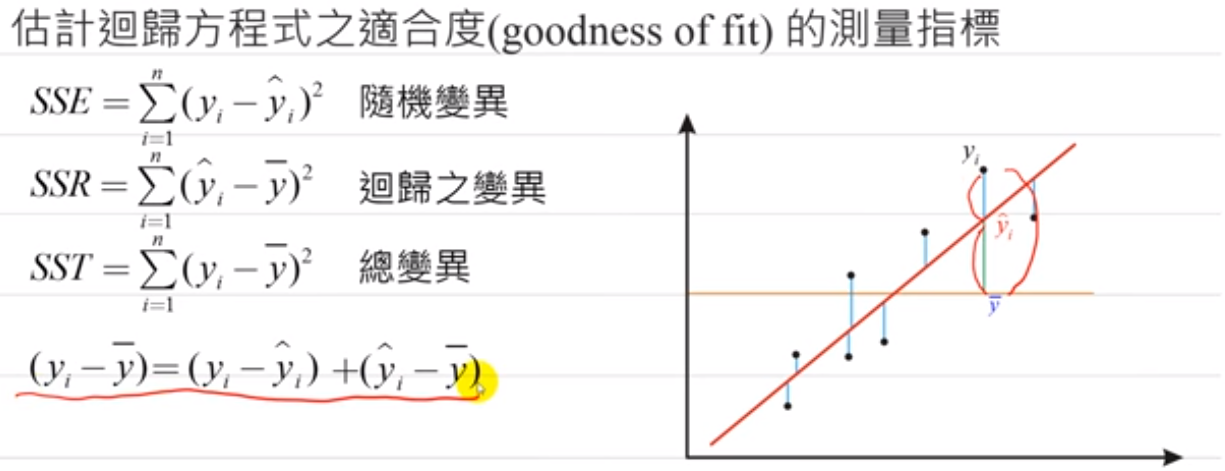

判定系数
SSE的其他表达方法
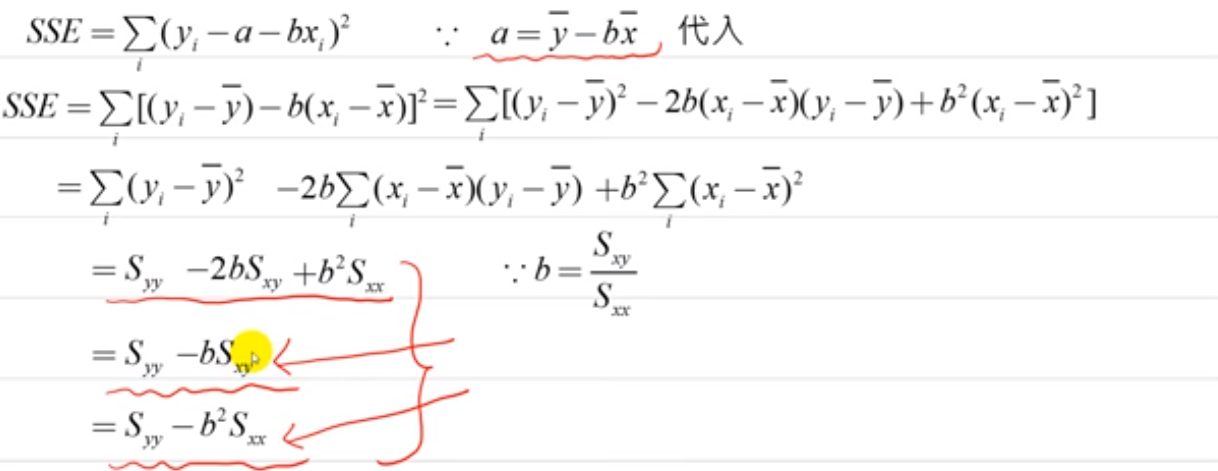
判定系数例题

内容归纳
若是判定系数不是很高,研究者应判断是否有残差很大的离群值(outlier)?若有,可将其排除后再重计算一次回归,可求得更合适的回归方程式(若有必要应解释离群值)
显著性检定

基本假设

变异数的估计

回归系数b之期望值

回归系数b之变异数
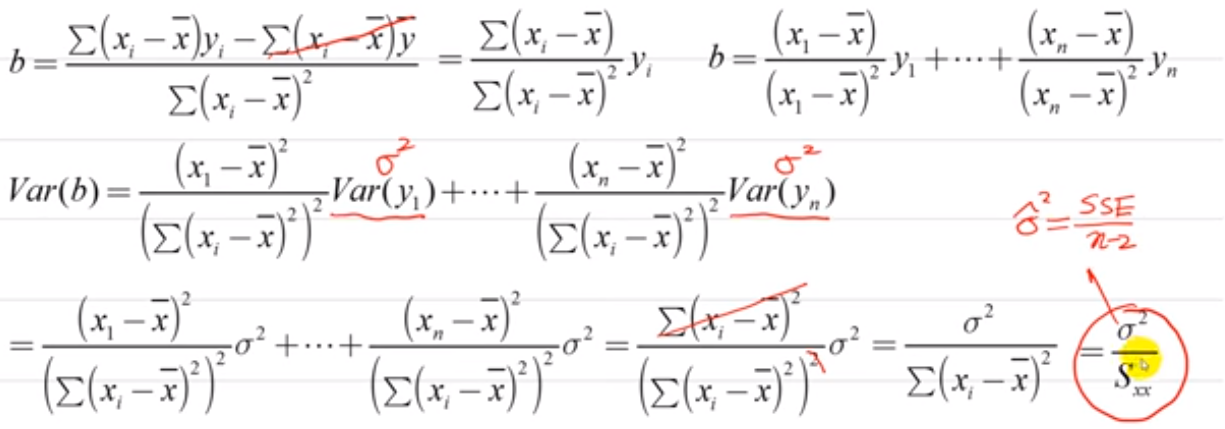
回归系数a之系数

回归系数之抽样分配

回归模型变异数估计示例
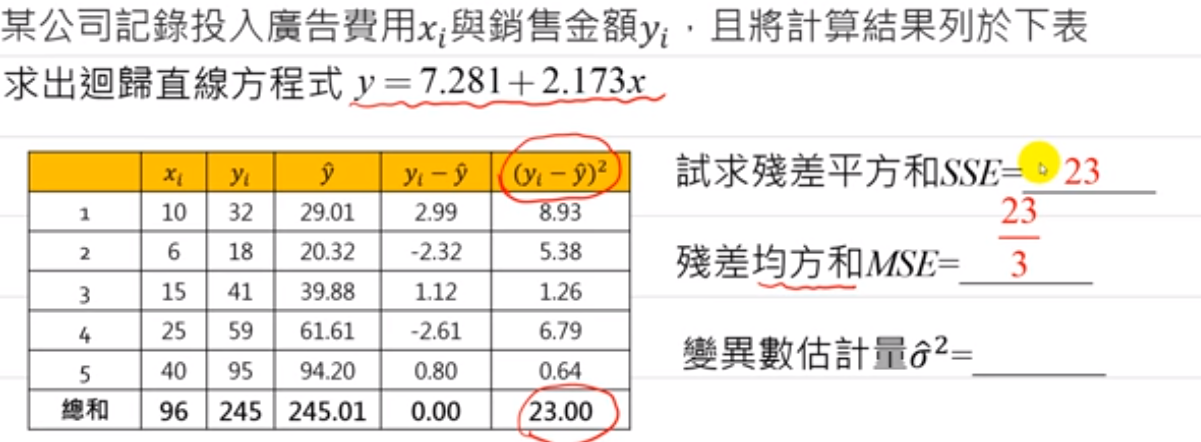
内容归纳
回归模型除了由判定系数判定模型的适合度外还需要检定模式的显著性。
