前言
推出一个新系列,《看图轻松理解数据结构和算法》,主要使用图片来描述常见的数据结构和算法,轻松阅读并理解掌握。本系列包括各种堆、各种队列、各种列表、各种树、各种图、各种排序等等几十篇的样子。
关于LSM树
LSM树,即日志结构合并树(Log-Structured Merge-Tree)。其实它并不属于一个具体的数据结构,它更多是一种数据结构的设计思想。大多NoSQL数据库核心思想都是基于LSM来做的,只是具体的实现不同。所以本来不打算列入该系列,但是有朋友留言了好几次让我讲LSM树,那么就说一下LSM树。
LSM树诞生背景
传统关系型数据库使用btree或一些变体作为存储结构,能高效进行查找。但保存在磁盘中时它也有一个明显的缺陷,那就是逻辑上相离很近但物理却可能相隔很远,这就可能造成大量的磁盘随机读写。随机读写比顺序读写慢很多,为了提升IO性能,我们需要一种能将随机操作变为顺序操作的机制,于是便有了LSM树。LSM树能让我们进行顺序写磁盘,从而大幅提升写操作,作为代价的是牺牲了一些读性能。
关于磁盘IO
磁盘读写时涉及到磁盘上数据查找,地址一般由柱面号、盘面号和块号三者构成。也就是说移动臂先根据柱面号移动到指定柱面,然后根据盘面号确定盘面的磁道,最后根据块号将指定的磁道段移动到磁头下,便可开始读写。
整个过程主要有三部分时间消耗,查找时间(seek time) +等待时间(latency time)+传输时间(transmission time) 。分别表示定位柱面的耗时、将块号指定磁道段移到磁头的耗时、将数据传到内存的耗时。整个磁盘IO最耗时的地方在查找时间,所以减少查找时间能大幅提升性能。
LSM树原理
LSM树由两个或以上的存储结构组成,比如在论文中为了方便说明使用了最简单的两个存储结构。一个存储结构常驻内存中,称为C0 tree,具体可以是任何方便健值查找的数据结构,比如红黑树、map之类,甚至可以是跳表。另外一个存储结构常驻在硬盘中,称为C1 tree,具体结构类似B树。C1所有节点都是100%满的,节点的大小为磁盘块大小。
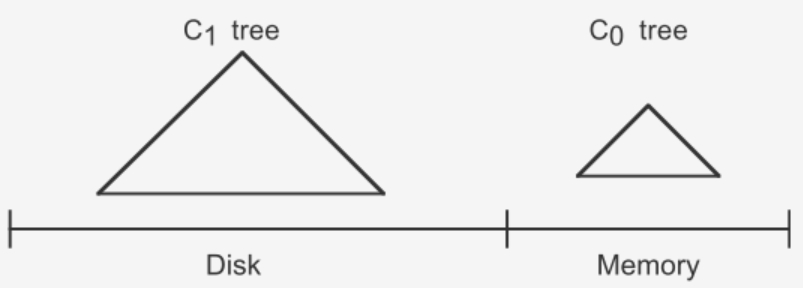
插入步骤
大体思路是:插入一条新纪录时,首先在日志文件中插入操作日志,以便后面恢复使用,日志是以append形式插入,所以速度非常快;将新纪录的索引插入到C0中,这里在内存中完成,不涉及磁盘IO操作;当C0大小达到某一阈值时或者每隔一段时间,将C0中记录滚动合并到磁盘C1中;对于多个存储结构的情况,当C1体量越来越大就向C2合并,以此类推,一直往上合并Ck。
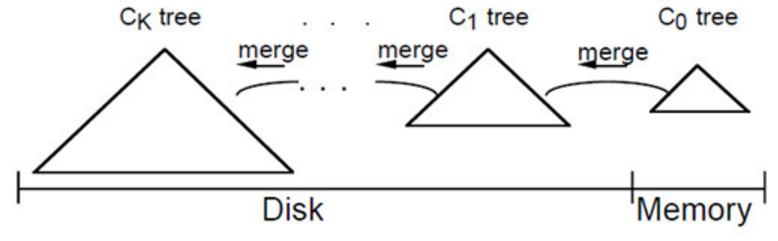
合并步骤
合并过程中会使用两个块:emptying block和filling block。
- 从C1中读取未合并叶子节点,放置内存中的emptying block中。
- 从小到大找C0中的节点,与emptying block进行合并排序,合并结果保存到filling block中,并将C0对应的节点删除。
- 不断执行第2步操作,合并排序结果不断填入filling block中,当其满了则将其追加到磁盘的新位置上,注意是追加而不是改变原来的节点。合并期间如故宫emptying block使用完了则再从C1中读取未合并的叶子节点。
- C0和C1所有叶子节点都按以上合并完成后即完成一次合并。
关于优化措施
本文用图阐述LSM的基本原理,但实际项目中其实有很多优化策略,而且有很多针对LSM树优化的paper。比如使用布隆过滤器快速判断key是否存在,还有做一些额外的索引以帮助更快找到记录等等。
插入操作
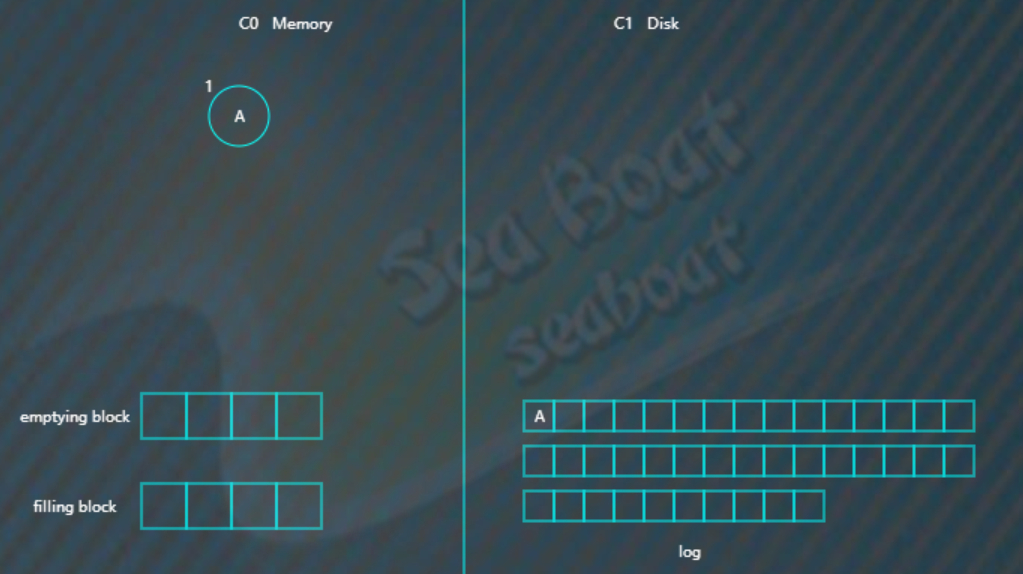
向LSM树中插入A E L R U,首先会插入到内存中的C0树上,这里使用AVL树,插入“A”,先项磁盘日志文件追加记录,然后再插入C0,
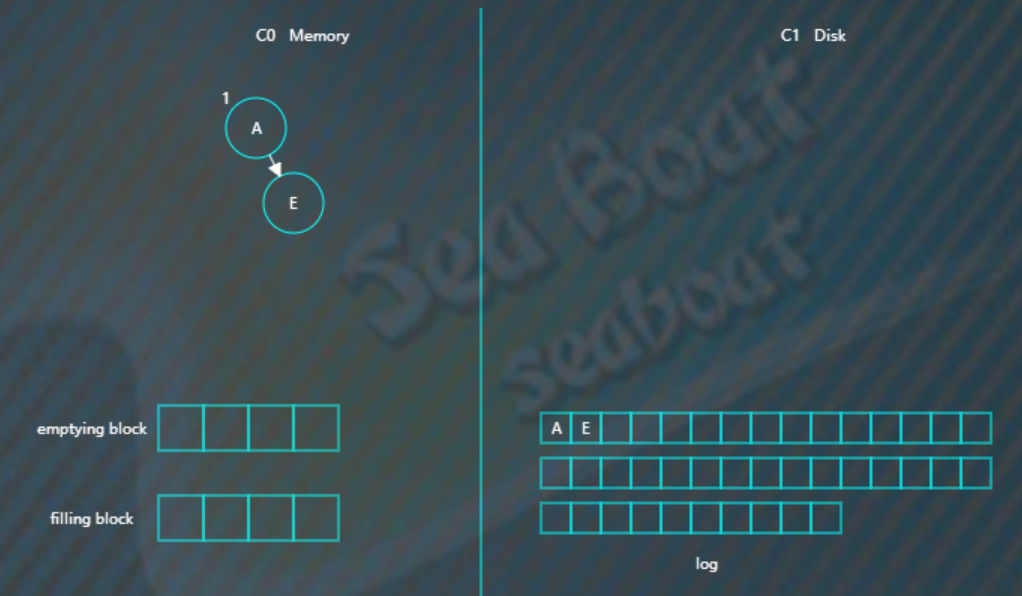
插入“E”,同样先追加日志再写内存,
继续插入“L”,旋转后如下,
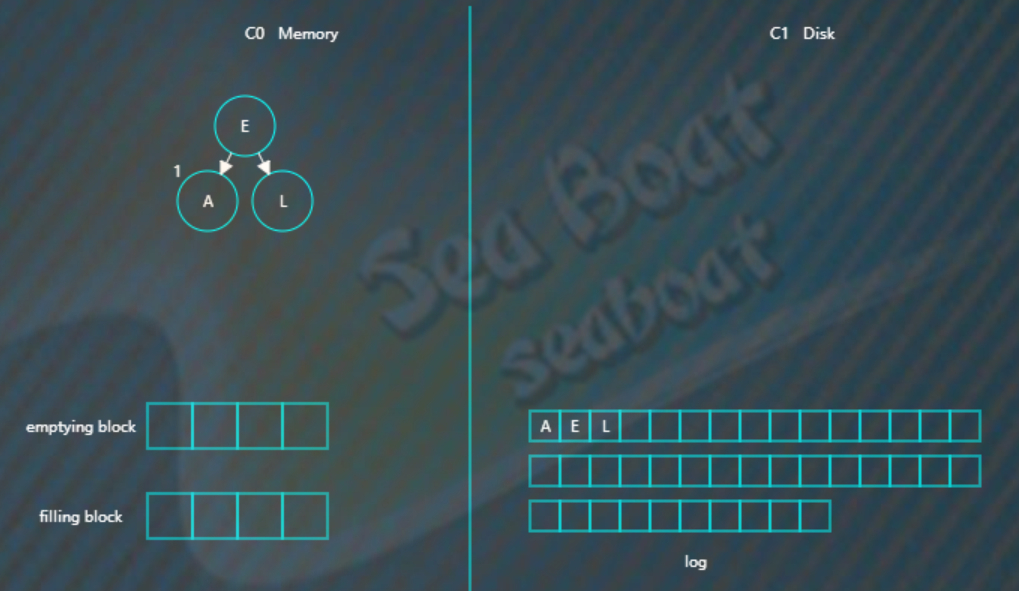
插入“R”“U”,旋转后最终如下。
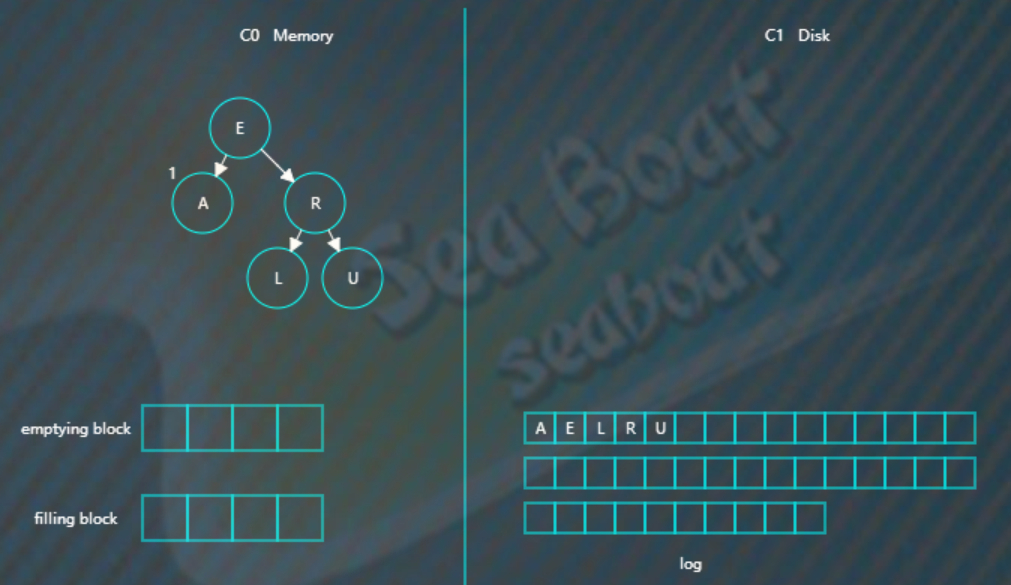
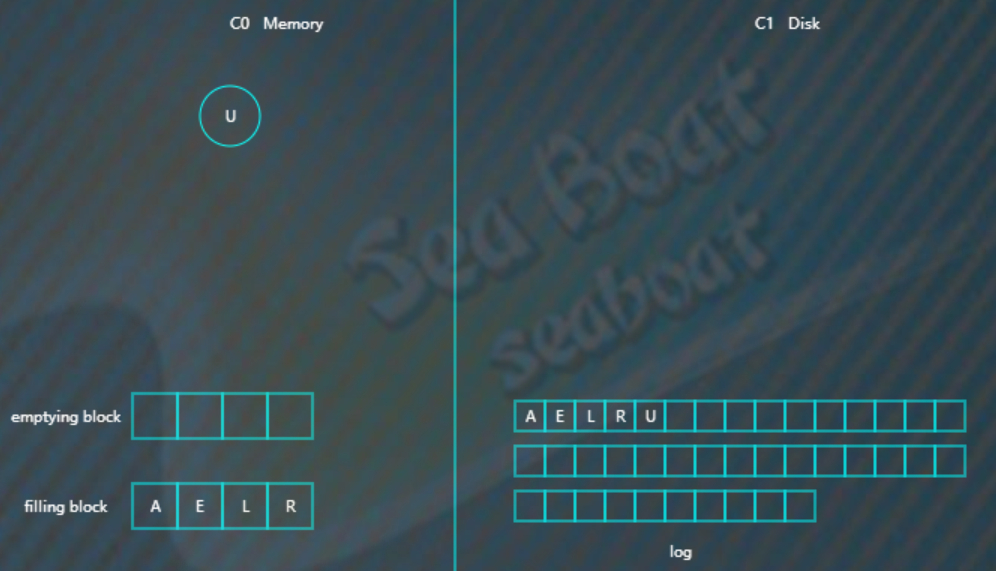
假设此时触发合并,则因为C1还没有树,所以emptying block为空,直接从C0树中依次找最小的节点。filling block长度为4,这里假设磁盘块大小为4。
开始找最小的节点,并放到filling block中,
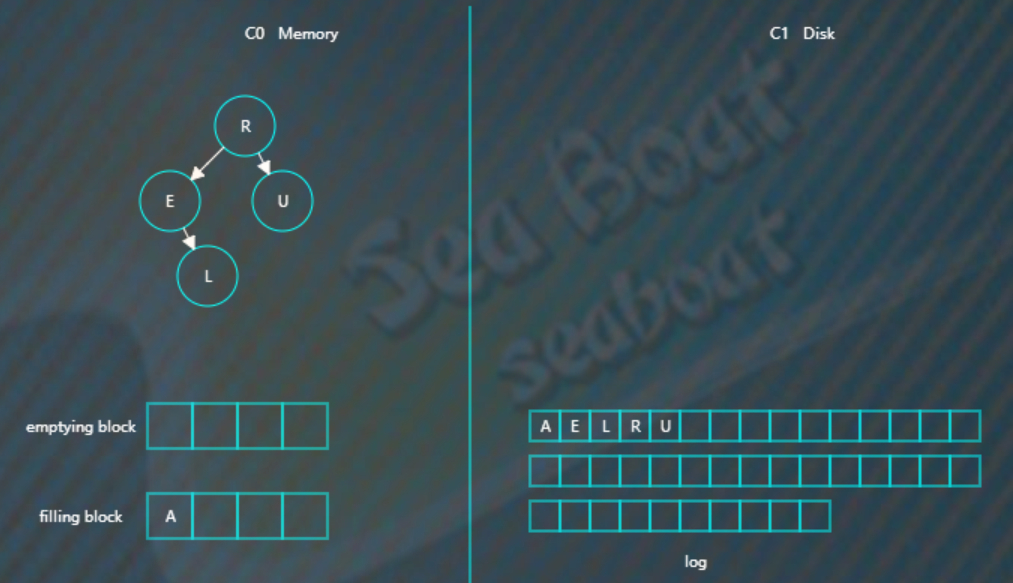
继续找第二个节点,
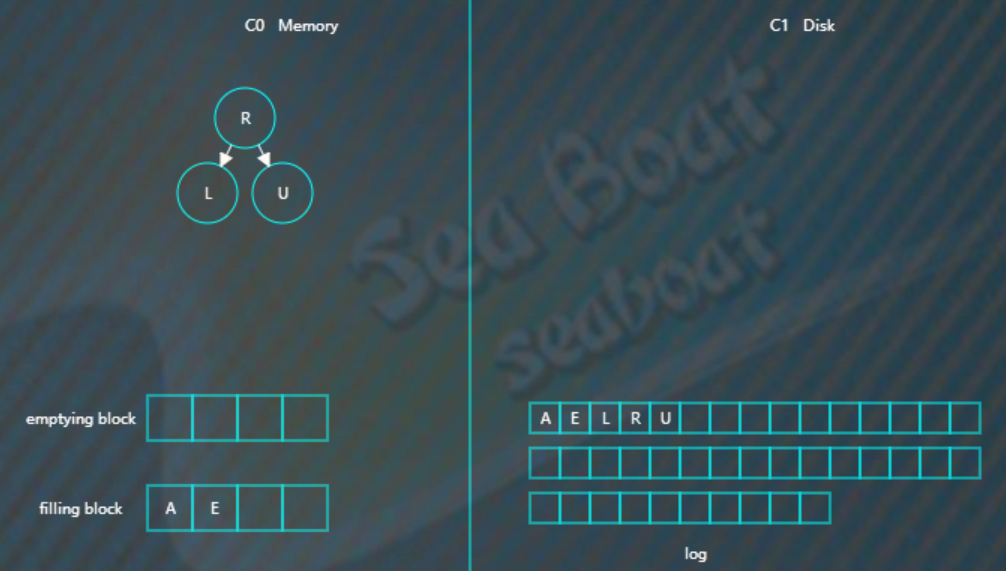
以此类推,填满filling block,
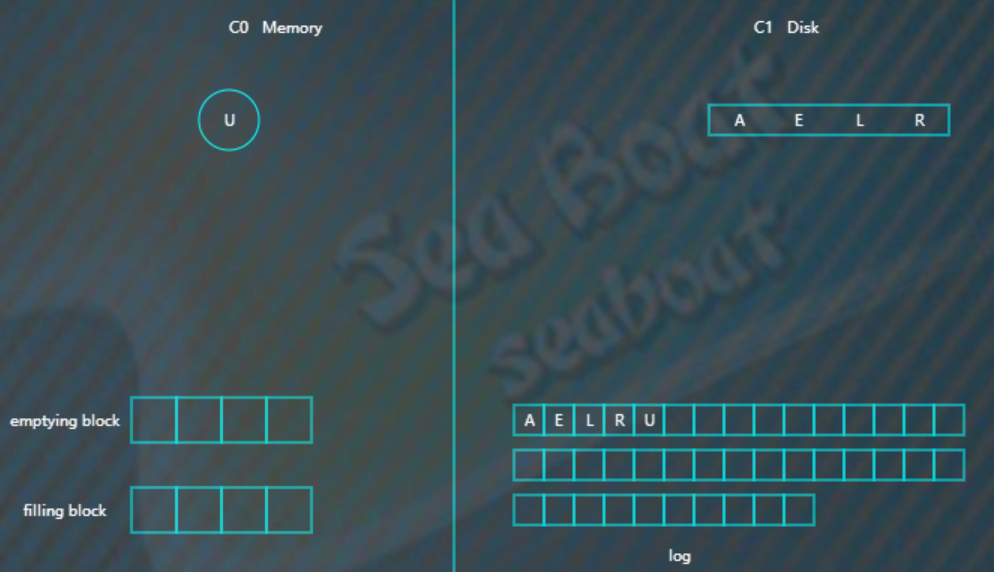
开始写入磁盘,C1树,
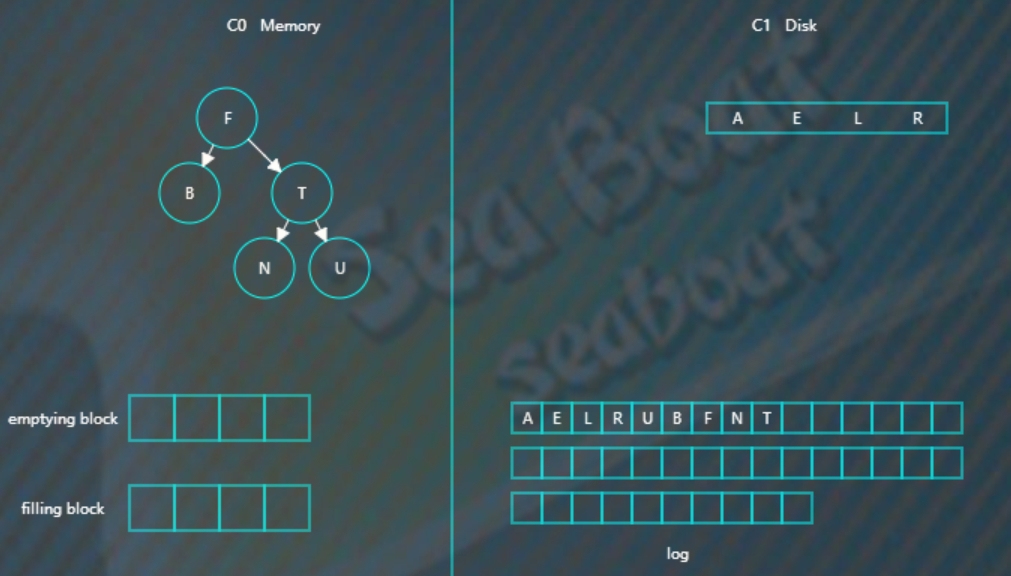
继续插入B F N T,先分别写日志,然后插入到内存的C0树中,
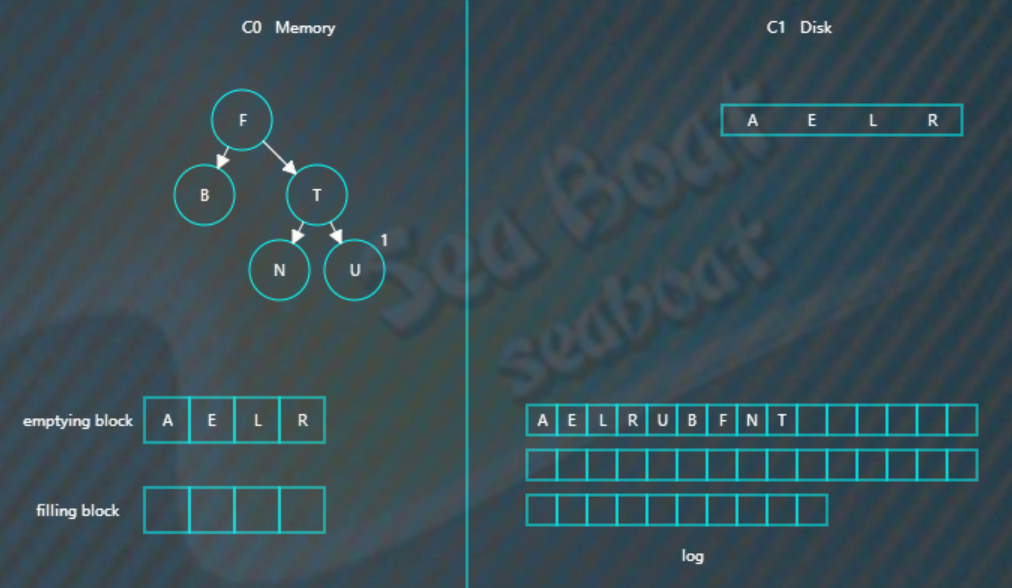
假如此时进行合并,先加载C1的最左边叶子节点到emptying block,
接着对C0树的节点和emptying block进行合并排序,首先是“A”进入filling block,
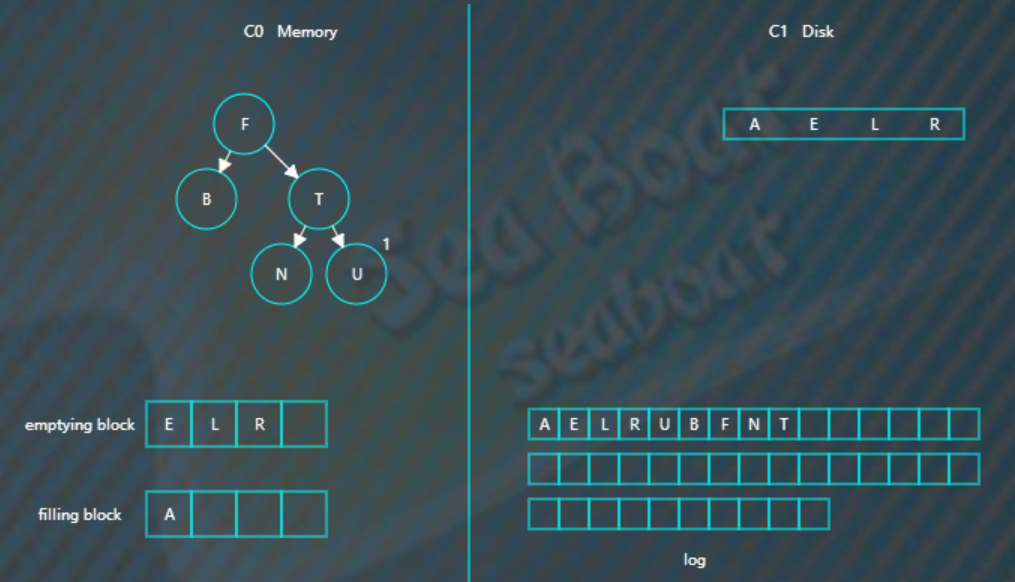
然后是“B”,
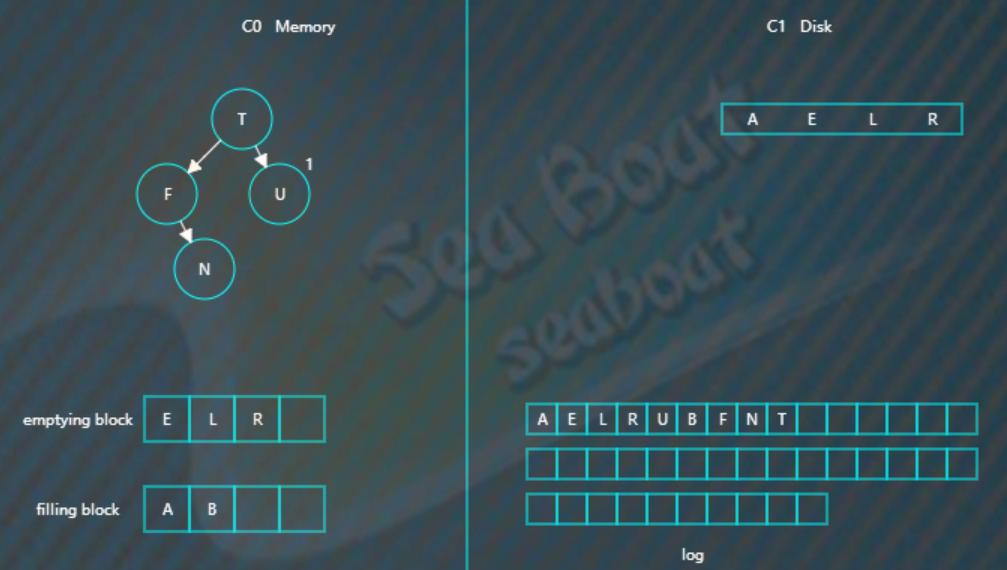
合并排序最终结果为,
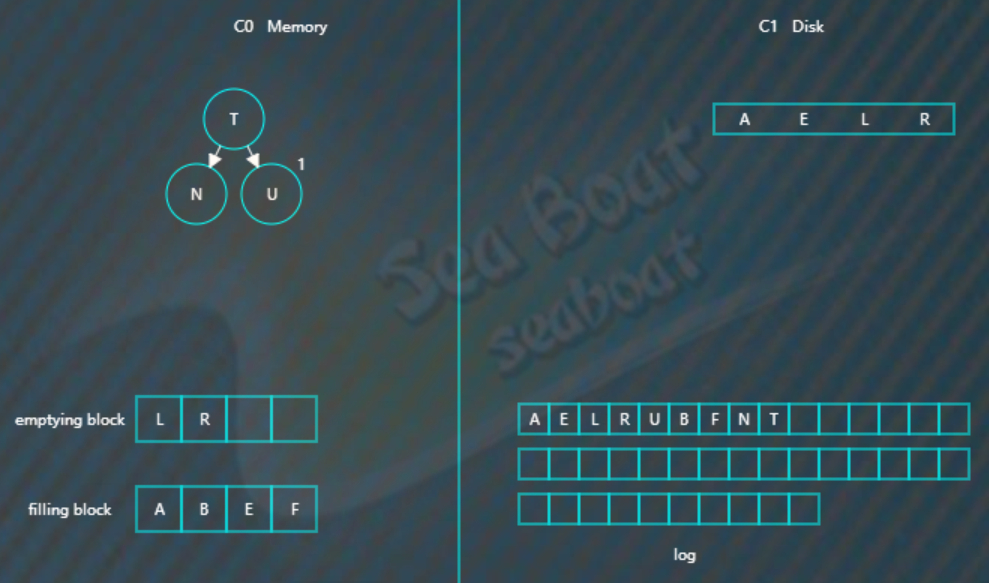
将filling block追加到磁盘的新位置,将原来的节点删除掉,
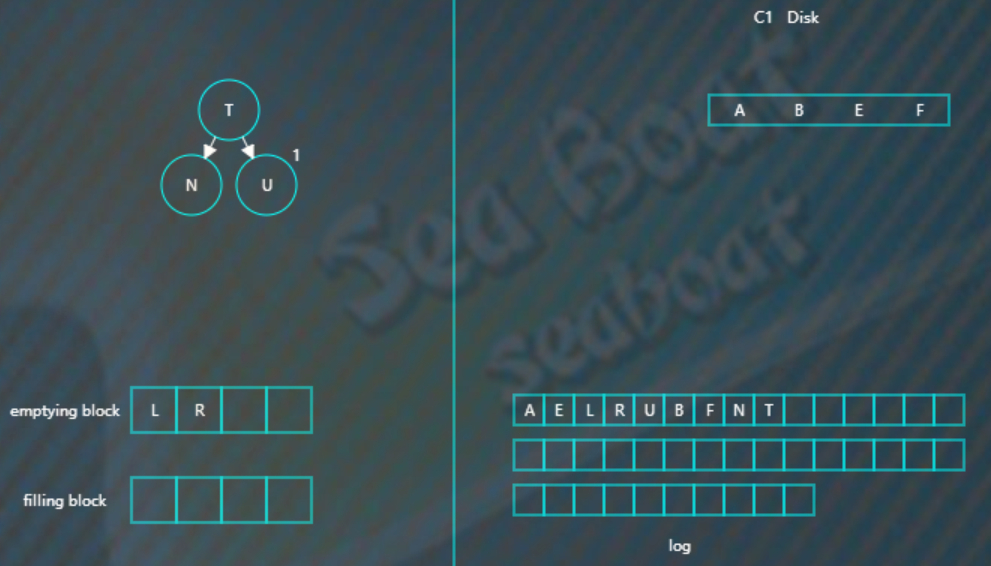
继续合并排序,再次填满filling block,
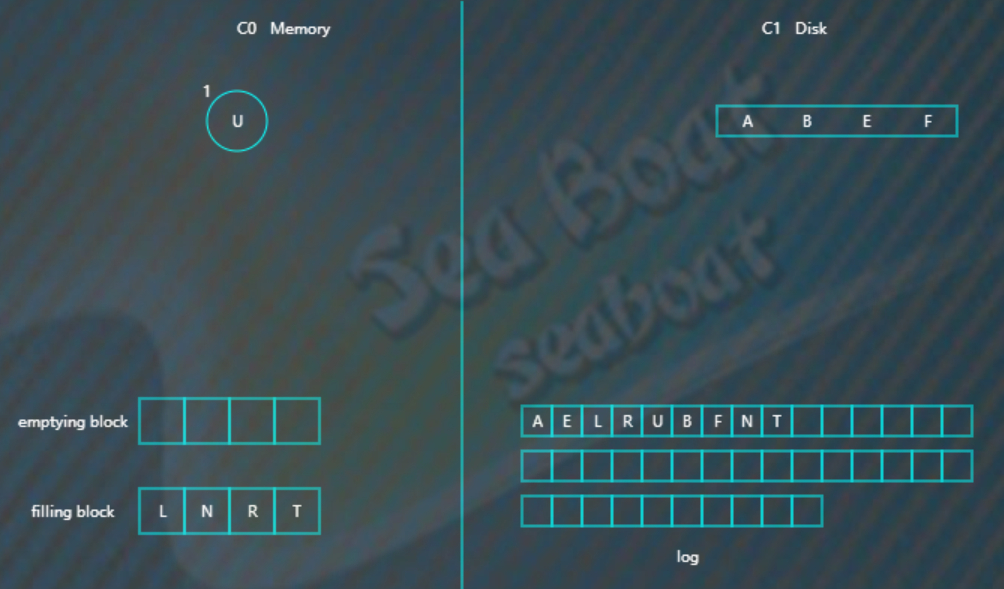
将filling block追加到磁盘的新位置,上一层的节点也要以磁盘块(或多个磁盘块)大小写入,尽量避开随机写。另外由于合并过程可能会导致上层节点的更新,可以暂时保存在内存,后面在适当时机写入。
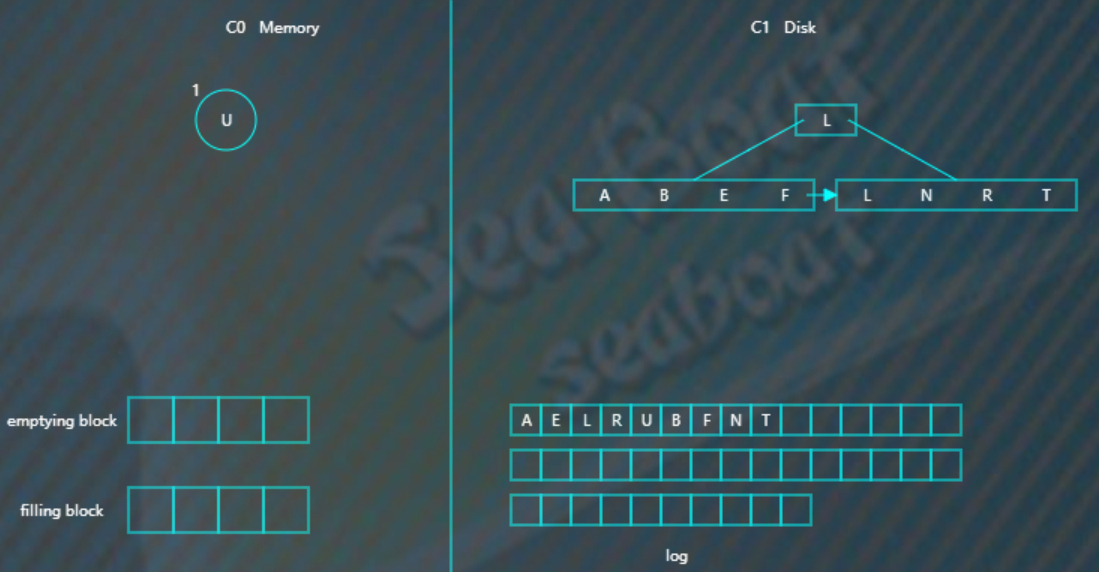
查找操作
查找总体思想是先找内存的C0树,找不到则找磁盘的C1树,然后是C2树,以此类推。
假如要找“B”,先找C0树,没找到。
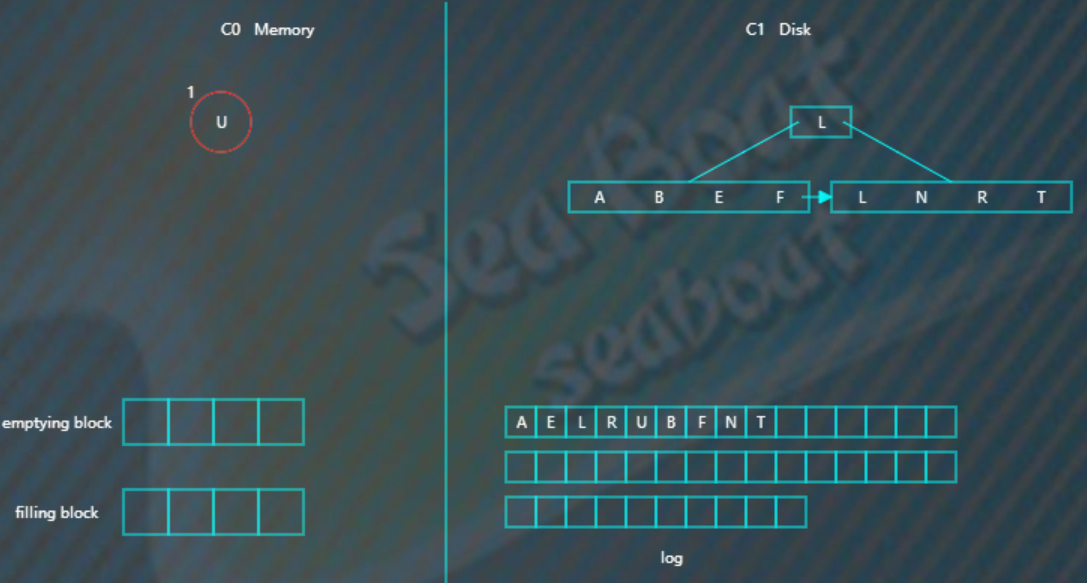
接着找C1树,从根节点开始,
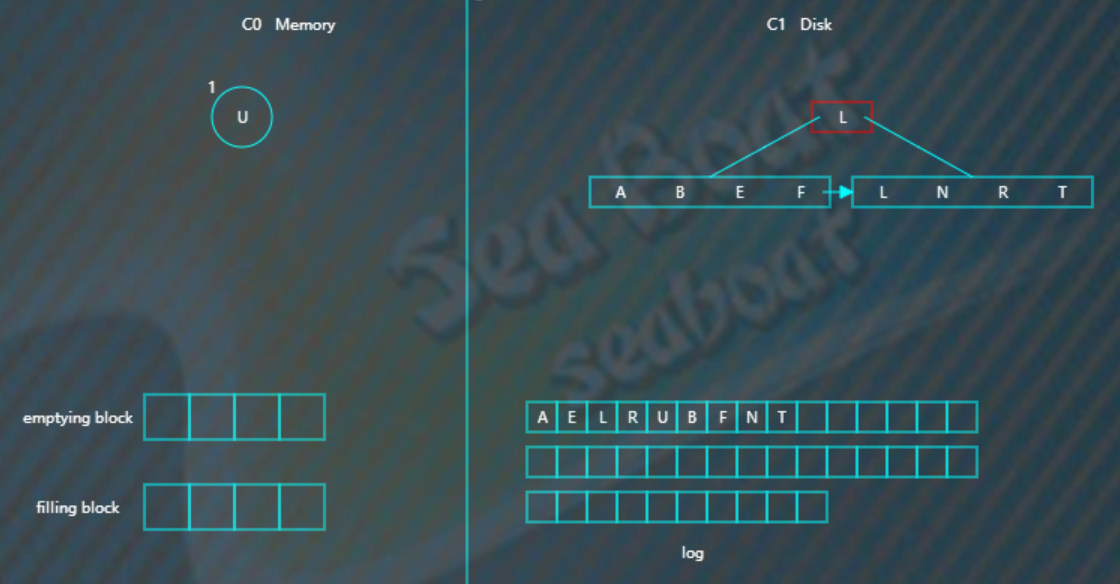
找到“B”。
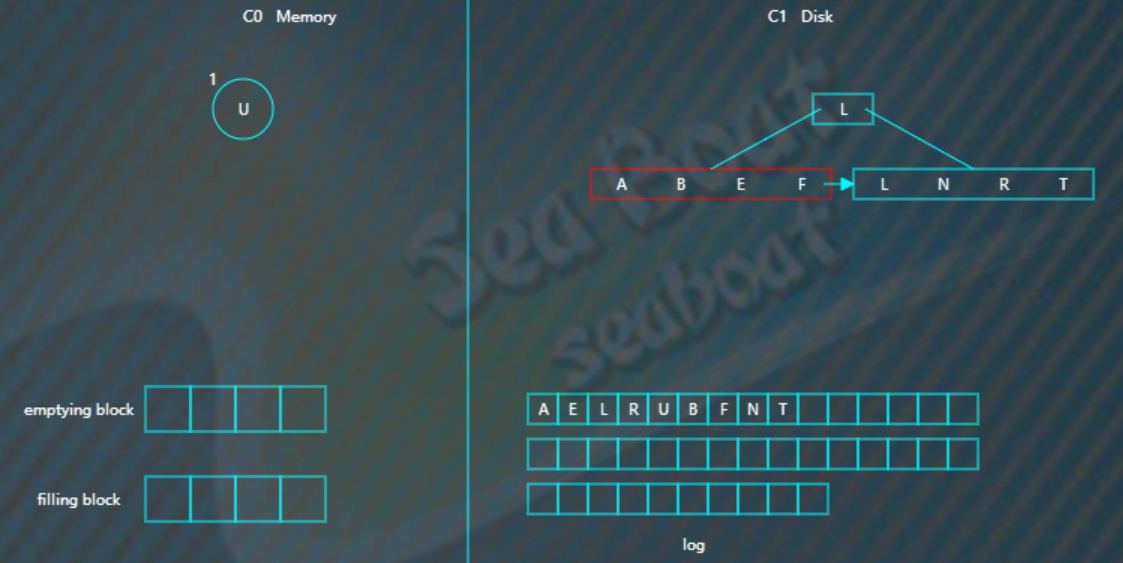
删除操作
删除操作为了能快速执行,主要是通过标记来实现,在内存中将要删除的记录标记一下,后面异步执行合并时将相应记录删除。
比如要删除“U”,假设标为#的表示删除,则C0树的“U”节点变为,
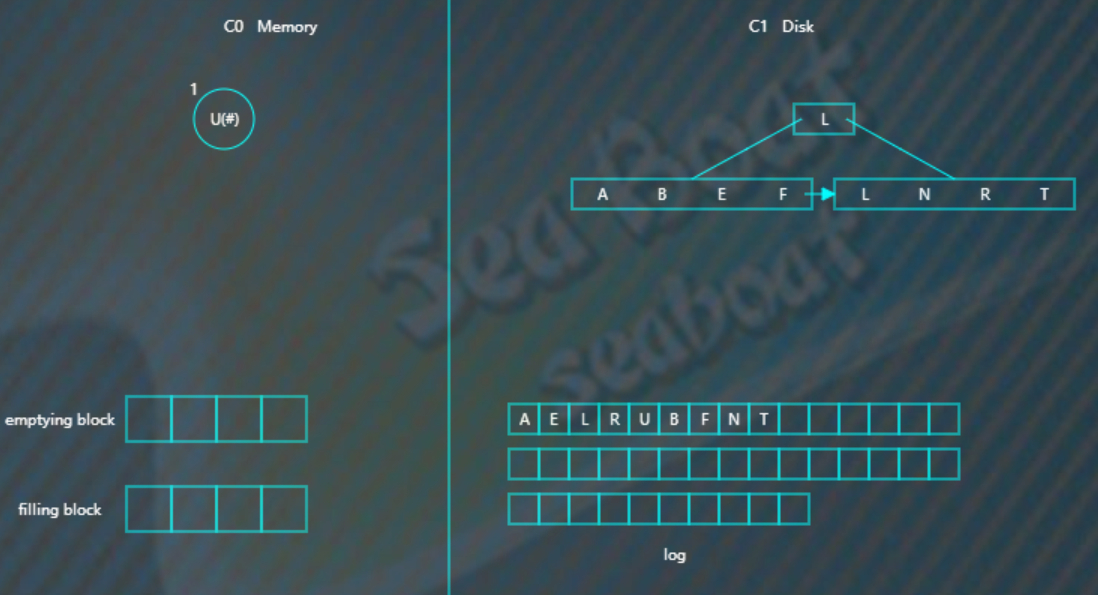
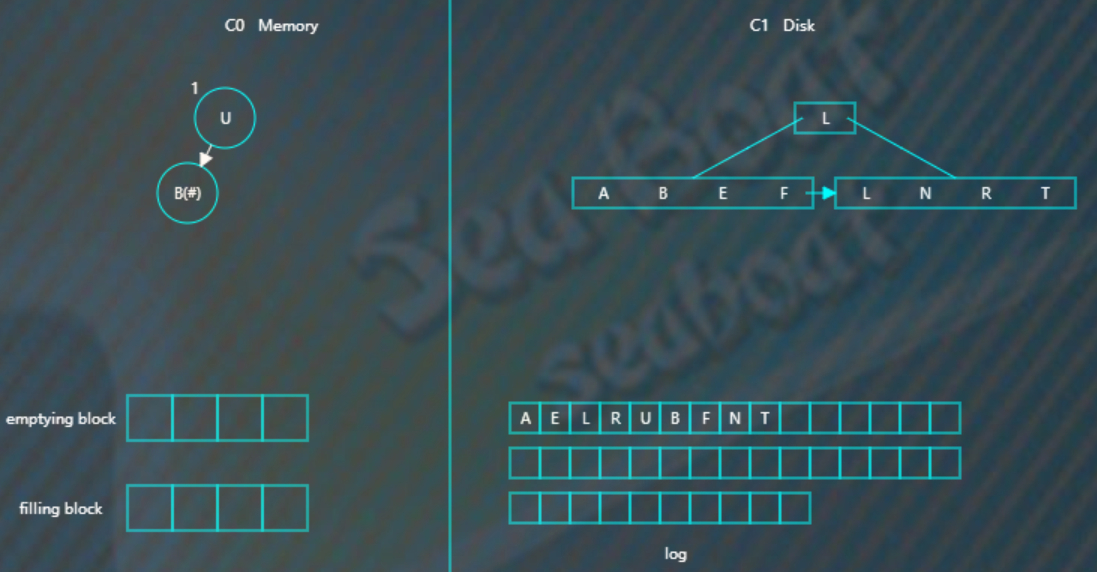
而如果C0树不存在的记录,则在C0树中生成一个节点,并标为#,查找时就能再内存中得知该记录已被删除,无需去磁盘找了。比如要删除“B”,那么没有必要去磁盘执行删除操作,直接在C0树中插入一个“B”节点,并标为#。
-------------推荐阅读------------
我的开源项目汇总(机器&深度学习、NLP、网络IO、AIML、mysql协议、chatbot)
跟我交流,向我提问:

欢迎关注:
