矩阵

自闭
382 阅读7分钟
原文链接： www.cnblogs.com

目录

 

update in 9.17

回到顶部

矩阵

并不想扯什么高端线代的内容因为我也不会

定义

由n \times m个数a_{ij}排成的 n行 m列的数表称为n行m列的矩阵，简称 n \times m矩阵。

A =⎡ ⎣⎢ ⎢⎢ a 11 a 21 , a 31 , a 41 a 12 … … … … a 1 m … … a n m ⎤ ⎦⎥ ⎥⎥ A=[a11a12…a1ma21,……a31,……a41…anm]

运算

这里只讲加法减法和乘法，其他的例如矩阵求逆等与本文内容出入较大，有兴趣的可以自己学习

加法

注意，只有行列均相同的矩阵才有加法！

运算也比较简单，把对应位置的数相加得到一个新的矩阵，即为答案

例如

[ 1 1 1 0 2 1 ] +[ 2 3 3 3 3 2 ] =[ 3 4 4 3 5 3 ] [112101]+[233332]=[345433]

加法满足以下运算律

A + B = B + A

(A + B) + C = A + (B + C)

减法

与加法同理。

乘法

这才是重点！！

两个矩阵能进行乘法的前提条件是：一个矩阵的行数等于另一个矩阵的列数

形式化的来说，若A是i \times k的矩阵，那么 B必须是 k \times j的矩阵！

他们相乘得到的C是i \times j的矩阵

其中C_{ij} = \sum_{i = 1}^n A_{ik} * B_{kj}

比如

[ 1 2 2 3 ] ×[ 2 3 4 4 5 3 ] =[ 8 13 12 20 11 19 ] [1223]×[245343]=[81211132019]

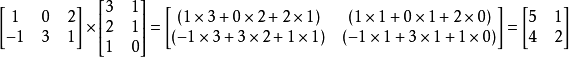
乘法满足结合律，左分配律，右分配律，即

(A \times B) \times C = A \times (B \times C)

(A + B) \times C = A \times C + B \times C

C(A + B) = C \times A + C \times B

千万注意！矩阵乘法不满足交换律！(很多情况下交换之后都不能相乘)

 

回到顶部

矩阵快速幂

因为矩阵有结合律，因此我们可以把整数的快速幂推广的矩阵上面

题目链接

同样是利用二进制倍增的思想，不难得到以下代码

其中的base，代表的是单位矩阵，也就是除了对角线全为1，其他位置都为0的矩阵，可以证明任意矩阵乘单位矩阵都等于自身

显然矩阵快速幂的复杂度为O(n^3 log k)

#include<cstdio>
#define LL long long 
using namespace std;
const int mod = 1e9 + 7;
int N;
LL K;
struct Matrix {
    int m[101][101];
    Matrix operator * (const Matrix &rhs) const {
        Matrix ans = {};
        for(int k = 1; k <= N; k++) 
            for(int i = 1; i <= N; i++) 
                for(int j = 1; j <= N; j++) 
                    (ans.m[i][j] += 1ll * m[i][k] * rhs.m[k][j] % mod) %= mod;
        return ans;
    }
};
Matrix fastpow(Matrix a, LL p) {
    Matrix base;
    for(int i = 1; i <= N; i++) base.m[i][i] = 1;//构造单位矩阵
    while(p) {
        if(p & 1) base = base * a;
        a = a * a; p >>= 1;
    }
    return base;
}
int main() {
    scanf("%d %lld", &N, &K);
    Matrix a; 
    for(int i = 1; i <= N; i++)    
        for(int j = 1; j <= N; j++)
            scanf("%d", &a.m[i][j]);
    a = fastpow(a, K);
    for(int i = 1; i <= N; i++, puts("")) 
        for(int j = 1; j <= N; j++)
            printf("%d ", a.m[i][j]);
    
    return 0;
}

 

回到顶部

应用

斐波那契数列第n项

矩阵快速幂最常见的应用就是优化递推啦

还是从最常见的斐波那契数列说起吧。

众周所知，斐波那契数列的递推公式为

f n =f n −1 +f n −2 ,f 1 =1 ,f 2 =1 fn=fn−1+fn−2,f1=1,f2=1

一般来说，这种看起来长得很萌简单，只与自身的函数值有关(可能带几个常数)的式子，一般都可以用矩阵快速幂来加速。

当然，如果你想找刺激，可以学一下这玩意儿

矩阵快速幂具体是怎么加速递推的呢？

首先我们把斐波那契数列写成矩阵的形式，因为f_n的取值与f_{n - 1}, f_{n - 2}这两项有关，因此我们需要同时保留这两项的值，我们不难得到一个 2 \times 1的矩阵

[ f n f n −1 ] [fnfn−1]

现在我们要进行递推，也就是得到这样一个矩阵

[ f n +1 f n ] [fn+1fn]

展开

[ f n +f n −1 f n ] [fn+fn−1fn]

观察一下，上面的一项需要用到f_{n}和f_{n - 1}，下面的一项只需要用到 f_n

同时结合上面的矩阵乘法的定义，我们不难得到一个转移矩阵

[ 1 1 1 0 ] [ f n f n −1 ] =[ f n +f n −1 f n ] [1110][fnfn−1]=[fn+fn−1fn]

这样我们乘一次即可递推到下一项。

但是这样好像并没有什么卵用啊，复杂度上还多了个矩阵相乘

嘿嘿

不要忘了，我们前面可以讲过矩阵有结合律的！

这样的话我们只需要把转移矩阵自乘n - 1次，然后再与初始矩阵相乘，就能得到答案矩阵啦！

题目链接

// luogu-judger-enable-o2
#include<cstdio>
#include<cstring>
#define LL long long 
using namespace std;
const int mod = 1e9 + 7;
LL K;
struct Matrix {
    int m[101][101], N;
    Matrix() {
        memset(m, 0, sizeof(m));
        N = 2;
    }
    Matrix operator * (const Matrix &rhs) const {
        Matrix ans;
        for(int k = 1; k <= N; k++) 
            for(int i = 1; i <= N; i++) 
                for(int j = 1; j <= N; j++) 
                    (ans.m[i][j] += 1ll * m[i][k] * rhs.m[k][j] % mod) %= mod;
        return ans;
    }
};
Matrix fastpow(Matrix a, LL p) {
    Matrix base; 
    for(int i = 1; i <= base.N; i++) base.m[i][i] = 1;//鏋勯€犲崟浣嶇煩闃?
    while(p) {
        if(p & 1) base = base * a;
        a = a * a; p >>= 1;
    }
    return base;
}
int main() {
    scanf("%lld", &K);
    Matrix a;
    a.m[1][1] = 1; a.m[1][2] = 1;
    a.m[2][1] = 1; a.m[2][2] = 0;
    a = fastpow(a, K - 1);
    printf("%d", a.m[1][1]);
    return 0;
}
代码

路径计数问题

https://www.nowcoder.com/acm/contest/185/B

给出一个 n * n 的邻接矩阵A. A是一个01矩阵 . A[i][j]=1表示i号点和j号点之间有长度为1的边直接相连. 求出从 1 号点 到 n 号点长度为k的路径的数目.

做法：直接对给出的矩阵快速幂k次，输出A[1][N]

解释：考虑矩阵相乘的过程，我们对于要计算的(i, j)位置，我们相当于是枚举了一个中间节点 k，来计算(i, k) * (k, j)

其他的常见矩阵推导

G i =a ×G i −1 +b ×G i −2 Gi=a×Gi−1+b×Gi−2

[ a 1 b 0 ] i −1 ×[ G 1 G 0 ] =[ a 1 b 0 ] ×[ G i −1 G i −2 ] =[ G i G i −1 ] [ab10]i−1×[G1G0]=[ab10]×[Gi−1Gi−2]=[GiGi−1]

 

G i =a ×G i −1 +i 2 Gi=a×Gi−1+i2

⎡ ⎣⎢ ⎢⎢ a 0 0 0 1 1 0 0 0 2 1 0 0 1 1 1 ⎤ ⎦⎥ ⎥⎥ i ×⎡ ⎣⎢ ⎢⎢ G 0 1 1 1 ⎤ ⎦⎥ ⎥⎥ =⎡ ⎣⎢ ⎢⎢ a 0 0 0 1 1 0 0 0 2 1 0 0 1 1 1 ⎤ ⎦⎥ ⎥⎥ ×⎡ ⎣⎢ ⎢⎢ G i −1 i 2 i 1 ⎤ ⎦⎥ ⎥⎥ =⎡ ⎣⎢ ⎢⎢ ⎢ G i ( i+ 1) 2 i +1 1 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ [a100012100110001]i×[G0111]=[a100012100110001]×[Gi−1i2i1]=[Gi(i+1)2i+11]

 

G i =a ×G i −1 +i 3 Gi=a×Gi−1+i3

⎡ ⎣⎢ ⎢⎢ ⎢⎢ ⎢ a 0 0 0 0 1 1 0 0 0 0 3 1 0 0 0 3 2 1 0 0 1 1 1 1 ⎤ ⎦⎥ ⎥⎥ ⎥⎥ ⎥ i ∗⎡ ⎣⎢ ⎢⎢ ⎢⎢ ⎢ G 0 1 1 1 1 ⎤ ⎦⎥ ⎥⎥ ⎥⎥ ⎥ =⎡ ⎣⎢ ⎢⎢ ⎢⎢ ⎢ a 0 0 0 0 1 1 0 0 0 0 3 1 0 0 0 3 2 1 0 0 1 1 1 1 ⎤ ⎦⎥ ⎥⎥ ⎥⎥ ⎥ × ⎡ ⎣⎢ ⎢⎢ ⎢⎢ ⎢ G i −1 i 3 i 2 i 1 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ = ⎡ ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ G i ( i + 1 ) 3 ( i + 1 ) 2 i + 1 1 ⎤ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ [ a 1 0 0 0 0 1 3 3 1 0 0 1 2 1 0 0 0 1 1 0 0 0 0 1 ] i ∗ [ G 0 1 1 1 1 ] = [ a 1 0 0 0 0 1 3 3 1 0 0 1 2 1 0 0 0 1 1 0 0 0 0 1 ] × [ G i − 1 i 3 i 2 i 1 ] = [ G i ( i + 1 ) 3 ( i + 1 ) 2 i + 1 1 ]

 

 

G i =a ×G i −1 +b i Gi=a×Gi−1+bi

[ a 0 1 b ] i ×[ G 0 b ] =[ a 0 1 b ] ×[ G i −1 b i ] =[ G i b i +1 ] [a10b]i×[G0b]=[a10b]×[Gi−1bi]=[Gibi+1]

 

 

回到顶部

参考资料

《深入浅出矩阵快速幂及其简单应用》

    作者：自为风月马前卒 个人博客attack204.com// 出处：zwfymqz.cnblogs.com/本文版权归作者和博客园共有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利。
avatar
文章
阅读
粉丝