为什么样本方差的分母是 n-1

2018-09-13 1,370 阅读2分钟

为什么样本方差的分母是 n-1

按照方差的定义，直观上我们可能会这样子计算方差：

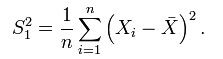
但是，在所有的书中，都将方差的计算公式定义为：

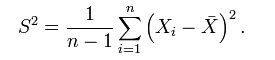
为什么是除以n-1而不是n呢？这就是这里要讨论的问题。

1、除n-1会带来什么问题

或许答案你已经知道了：为了保证方差估计的无偏性，我们通常要除以n-1，而不是n.如果是除以n，会使得估计的方差比实际方差要小。这是为什么呢？我们下面就来讨论讨论

1.1 现实生活中面临的问题

加入我们要调查全国人民的收入水平，并且已经知道了全国人民的平均收入水平问 $\mu$ （别问我为什么知道的，上帝告诉我的）。这时我们对总体进行抽样，记每个样本问 $X_{i}$ ，根据的定义，我们可以得到全国人民收入水平的方差为:

\mathbb{E}\Big[\frac{1}{n} \sum_{i=1}^n\Big(X_i -\mu\Big)^2 \Big]=\sigma^2

但问题是，现实生活中， $\mu$ 是无法确定的(你不可能调查到所有人的收入水平)。这时候，我们就会用样本的均值 $\bar{X}$ 去代替 $\mu$ 。但是！

如果直接使用 $\frac{1}{n} \sum_{i=1}^n\Big(X_i -\bar{X}\Big)^2$ 作为方差的估计，那么计算出来的结果会低于实际的方差！

这是因为：

\begin{eqnarray}\frac{1}{n}\sum_{i=1}^n(X_i-\bar{X})^2 &=&\frac{1}{n}\sum_{i=1}^n\Big[(X_i-\mu) + (\mu -\bar{X}) \Big]^2\\&=&\frac{1}{n}\sum_{i=1}^n(X_i-\mu)^2 +\frac{2}{n}\sum_{i=1}^n(X_i-\mu)(\mu -\bar{X})+\frac{1}{n}\sum_{i=1}^n(\mu -\bar{X})^2 \\&=&\frac{1}{n}\sum_{i=1}^n(X_i-\mu)^2 +2(\bar{X}-\mu)(\mu -\bar{X})+(\mu -\bar{X})^2 \\&=&\frac{1}{n}\sum_{i=1}^n(X_i-\mu)^2 -(\mu -\bar{X})^2 \end{eqnarray}

换言之，除非正好 $\bar{X}=\mu$ ，否则我们一定有

\frac{1}{n}\sum_{i=1}^n(X_i-\bar{X})^2 <\frac{1}{n}\sum_{i=1}^n(X_i-\mu)^2

而不等式右边的那位才是的对方差的“正确”估计！这个不等式说明了，为什么直接使用 $\frac{1}{n} \sum_{i=1}^n\Big(X_i -\bar{X}\Big)^2$ 会导致对方差的低估。

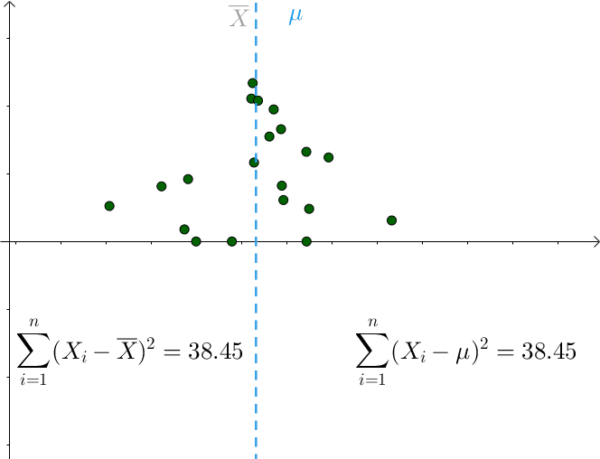
我们通过一个gif来看一下， $\bar{X}$ 和 $\mu$ 的实际偏差越大，对估计的影响就越大！

1.2 如何解决这个问题

那么，在不知道随机变量真实数学期望的前提下，如何“正确”的估计方差呢？答案是把上式中的分母 $n$ ，通过这种方法把原来的偏小的估计“放大”一点点，我们就能获得对方差的正确估计了：

\mathbb{E}\Big[\frac{1}{n-1} \sum_{i=1}^n\Big(X_i -\bar{X}\Big)^2\Big]=\mathbb{E}\Big[\frac{1}{n} \sum_{i=1}^n\Big(X_i -\mu\Big)^2 \Big]=\sigma^2.

至于为什么分母是n-1而不是n-2或者别的什么数呢？这就是我们接下来要证明的事情。

2、调整分母得到无偏估计

设 $S^{2}$ 为我们估计的方差，则

{\displaystyle {\begin{aligned} \operatorname {E} [S^{2}]& =\operatorname {E} \left[{\frac{1}{n}}\sum _{i=1}^{n}{\big (}X_{i}-{\overline{X}}{\big )}^{2}\right]=\operatorname {E} {\bigg[}{\frac{1}{n}}\sum _{i=1}^{n}{\bigg(}(X_{i}-\mu )-({\overline{X}}-\mu ){\bigg)}^{2}{\bigg]}\\[8pt]& =\operatorname {E} {\bigg[}{\frac{1}{n}}\sum _{i=1}^{n}{\bigg(}(X_{i}-\mu )^{2}-2({\overline{X}}-\mu )(X_{i}-\mu )+({\overline{X}}-\mu )^{2}{\bigg)}{\bigg]}\\[8pt]& =\operatorname {E} {\bigg[}{\frac{1}{n}}\sum _{i=1}^{n}(X_{i}-\mu )^{2}-{\frac{2}{n}}({\overline{X}}-\mu )\sum _{i=1}^{n}(X_{i}-\mu )+{\frac{1}{n}}({\overline{X}}-\mu )^{2}\sum _{i=1}^{n}1{\bigg]}\\[8pt]& =\operatorname {E} {\bigg[}{\frac{1}{n}}\sum _{i=1}^{n}(X_{i}-\mu )^{2}-{\frac{2}{n}}({\overline{X}}-\mu )\sum _{i=1}^{n}(X_{i}-\mu )+{\frac{1}{n}}({\overline{X}}-\mu )^{2}\cdot n{\bigg]}\\[8pt]& =\operatorname {E} {\bigg[}{\frac{1}{n}}\sum _{i=1}^{n}(X_{i}-\mu )^{2}-{\frac{2}{n}}({\overline{X}}-\mu )\sum _{i=1}^{n}(X_{i}-\mu )+({\overline{X}}-\mu )^{2}{\bigg]}\\[8pt]\end{aligned}}}

其中：

{\displaystyle {\begin{aligned} {\overline{X}}-\mu ={\frac{1}{n}}\sum _{i=1}^{n}X_{i}-\mu ={\frac{1}{n}}\sum _{i=1}^{n}X_{i}-{\frac{1}{n}}\sum _{i=1}^{n}\mu \ ={\frac{1}{n}}\sum _{i=1}^{n}(X_{i}-\mu ).\\[8pt]\end{aligned}}}

所以我们接着算下去：

{\displaystyle {\begin{aligned} \operatorname {E} [S^{2}]& =\operatorname {E} {\bigg[}{\frac{1}{n}}\sum _{i=1}^{n}(X_{i}-\mu )^{2}-{\frac{2}{n}}({\overline{X}}-\mu )\sum _{i=1}^{n}(X_{i}-\mu )+({\overline{X}}-\mu )^{2}{\bigg]}\\[8pt]& =\operatorname {E} {\bigg[}{\frac{1}{n}}\sum _{i=1}^{n}(X_{i}-\mu )^{2}-{\frac{2}{n}}({\overline{X}}-\mu )\cdot n\cdot ({\overline{X}}-\mu )+({\overline{X}}-\mu )^{2}{\bigg]}\\[8pt]& =\operatorname {E} {\bigg[}{\frac{1}{n}}\sum _{i=1}^{n}(X_{i}-\mu )^{2}-2({\overline{X}}-\mu )^{2}+({\overline{X}}-\mu )^{2}{\bigg]}\\[8pt]& =\operatorname {E} {\bigg[}{\frac{1}{n}}\sum _{i=1}^{n}(X_{i}-\mu )^{2}-({\overline{X}}-\mu )^{2}{\bigg]}\\[8pt]& =\operatorname {E} {\bigg[}{\frac{1}{n}}\sum _{i=1}^{n}(X_{i}-\mu )^{2}{\bigg]}-\operatorname {E} {\bigg[}({\overline{X}}-\mu )^{2}{\bigg]}\\[8pt]& =\sigma ^{2}-\operatorname {E} \left[({\overline{X}}-\mu )^{2}\right]\end{aligned}}}

其中(证明见：这里)：

\operatorname {E} \left[({\overline{X}}-\mu )^{2}\right]=\frac{1}{n}\sigma^{2}

所以：

E[\frac{1}{n}\sum _{i=1}^{n}(X_ i-\overline{X})^2]=\sigma ^{2}-{\frac{1}{n}}\sigma ^{2}=\frac{n-1}{n}\sigma ^{2}

也就是说，低估了 $\displaystyle {\frac{1}{n}}\sigma ^{2}$ ，进行一下调整：

\frac{n}{n-1}E[\frac{1}{n}\sum _{i=1}^{n}(X_ i-\overline{X})^2]=E[\frac{1}{n-1}\sum _{i=1}^{n}(X_ i-\overline{X})^2]=\sigma ^{2}

因此使用下面这个式子进行估计，得到的就是无偏估计：

S^2=\frac{1}{n-1}\sum _{i=1}^{n}(X_ i-\overline{X})^2