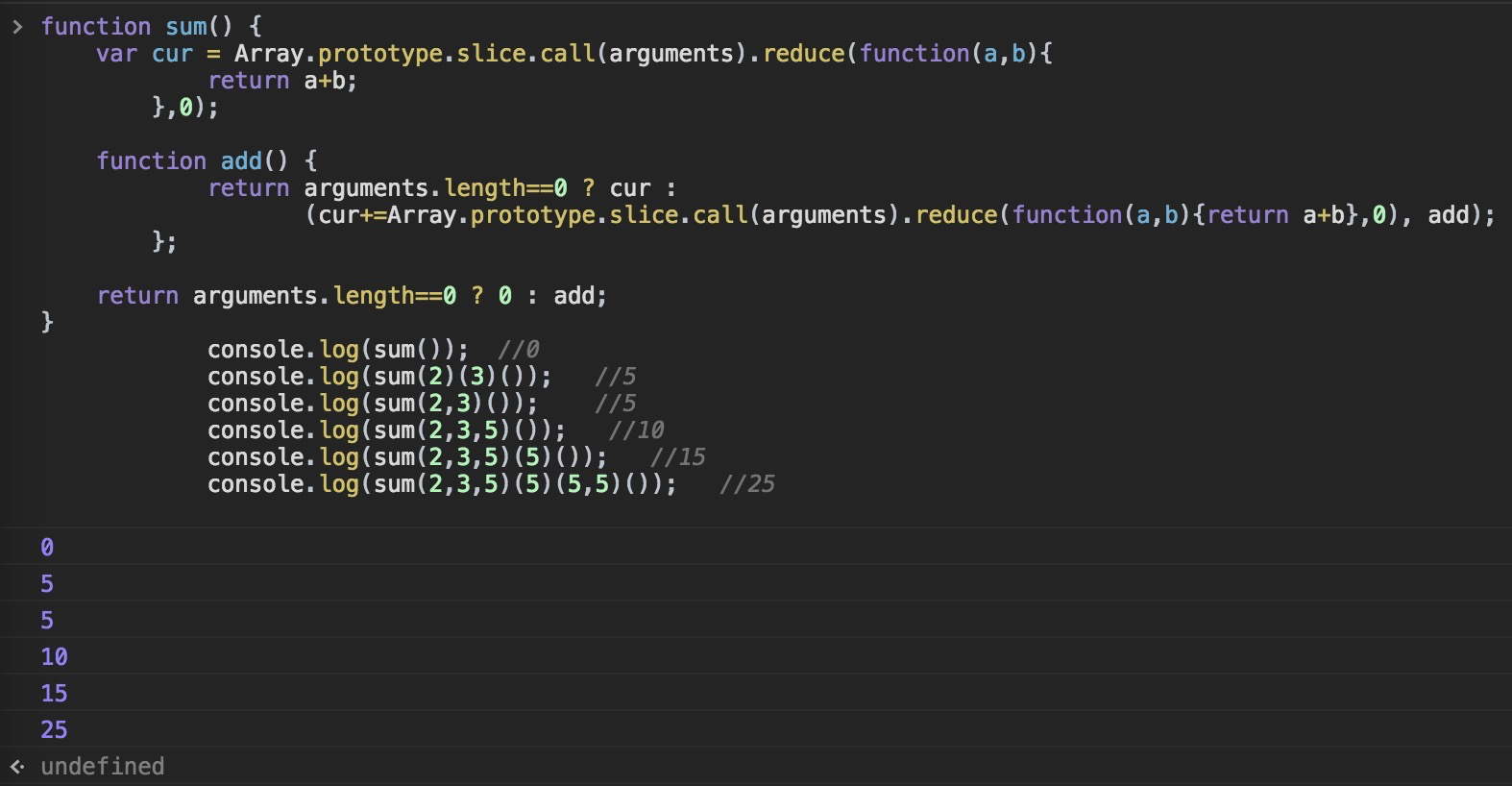
题目1:
有时候我们需要访问一个对象较深的层次,但是如果这个对象某个属性不存在的话就会报错,例如:
var data = { a: { b: { c: 'ScriptOJ' } } }
data.a.b.c // => scriptoj
data.a.b.c.d // => 报错,代码停止执行console.log('ScriptOJ') // => 不会被执行
请你完成一个 safeGet 函数,可以安全的获取无限多层次的数据,一旦数据不存在不会报错,会返回 undefined,
例如:
var data = { a: { b: { c: 'ScriptOJ' } } }
safeGet(data, 'a.b.c') // => scriptoj
safeGet(data, 'a.b.c.d') // => 返回 undefined
safeGet(data, 'a.b.c.d.e.f.g') // => 返回 undefinedconsole.log('ScriptOJ') // => 打印 ScriptOJ
答案:
const safeGet = (o, path) => {
try {
return path.split('.').reduce((o, k) => o[k], o)
} catch (e) {
return void 666
}
}
转载自从一道面试题认识函数柯里化
题目2
如何实现 multi(2)(3)(4)=24?
首先来分析下这道题,实现一个 multi 函数并依次传入参数执行,得到最终的结果。通过题目很容易得到的结论是,把传入的参数相乘就能够得到需要的结果,也就是 2X3X4 = 24。
简单的实现
那么如何实现 multi 函数去计算出结果值呢?脑海中首先浮现的解决方案是,闭包。
function multi(a) {
return function(b) {
return function(c) {
return a * b * c;
}
}
}
复制代码利用闭包的原则,multi 函数执行的时候,返回 multi 函数中的内部函数,再次执行的时候其实执行的是这个内部函数,这个内部函数中接着又嵌套了一个内部函数,用于计算最终结果并返回。
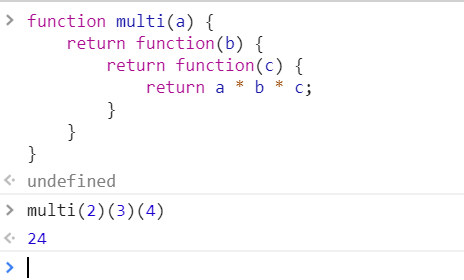
单纯从题面来说,似乎是已经实现了想要的结果,但仔细一想就会发现存在问题。
上面的实现方案存在的缺陷:
- 代码不够优雅,实现步骤需要一层一层的嵌套函数。
- 可扩展性差,假如是要实现 multi(2)(3)(4)...(n) 这样的功能,那就得嵌套 n 层函数。
那么有没有更好的解决方案,答案是,使用函数式编程中的函数柯里化实现。
函数柯里化
在函数式编程中,函数是一等公民。那么函数柯里化是怎样的呢?
函数柯里化指的是将能够接收多个参数的函数转化为接收单一参数的函数,并且返回接收余下参数且返回结果的新函数的技术。
函数柯里化的主要作用和特点就是参数复用、提前返回和延迟执行。
例如:封装兼容现代浏览器和 IE 浏览器的事件监听的方法,正常情况下封装是这样的。
var addEvent = function(el, type, fn, capture) {
if(window.addEventListener) {
el.addEventListener(type, function(e) {
fn.call(el, e);
}, capture);
}else {
el.attachEvent('on' + type, function(e) {
fn.call(el, e);
})
}
}
复制代码该封装的方法存在的不足是,每次写监听事件的时候调用 addEvent 函数,都会进行 if else 的兼容性判断。事实上在代码中只需要执行一次兼容性判断就可以了,后续的事件监听就不需要再去判断兼容性了。那么怎么用函数柯里化优化这个封装函数。
var addEvent = (function() {
if(window.addEventListener) {
return function(el, type, fn, capture) {
el.addEventListener(type, function(e) {
fn.call(el, e);
}, capture);
}
}else {
return function(ele, type, fn) {
el.attachEvent('on' + type, function(e) {
fn.call(el, e);
})
}
}
})()
复制代码js 引擎在执行该段代码的时候就会进行兼容性判断,并且返回需要使用的事件监听封装函数。这里使用了函数柯里化的两个特点:提前返回和延迟执行。
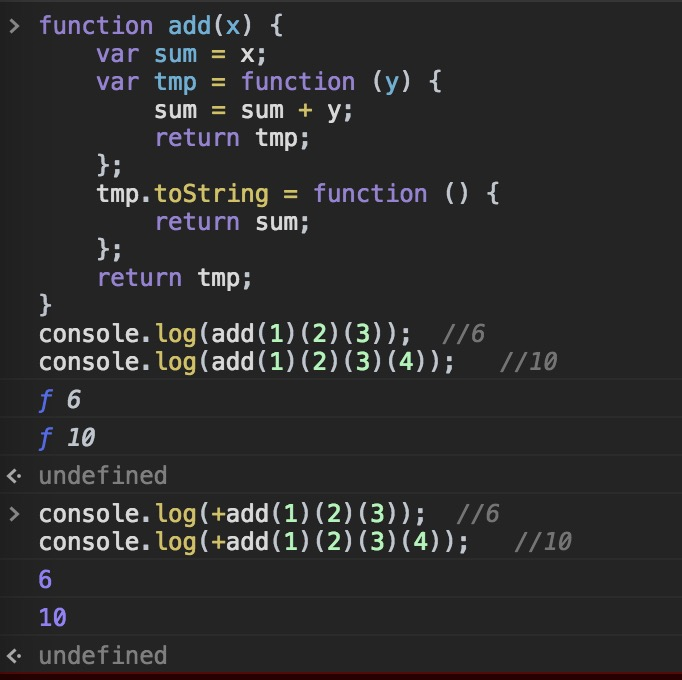
柯里化另一个典型的应用场景就是 bind 函数的实现。使用了函数柯里化的两个特点:参数复用和提前返回。
Function.prototype.bind = function(){
var fn = this;
var args = Array.prototye.slice.call(arguments);
var context = args.shift();
<span class="hljs-keyword">return</span> <span class="hljs-function"><span class="hljs-keyword">function</span>(<span class="hljs-params"></span>)</span>{
<span class="hljs-keyword">return</span> fn.apply(context, args.concat(<span class="hljs-built_in">Array</span>.prototype.slice.call(<span class="hljs-built_in">arguments</span>)));
};
};
复制代码
柯里化的实现
那么如何通过函数柯里化实现面试题的功能呢?
通用版
function curry(fn) {
var args = Array.prototype.slice.call(arguments, 1);
return function() {
var newArgs = args.concat(Array.prototype.slice.call(arguments));
return fn.apply(this, newArgs);
}
}
复制代码curry 函数的第一个参数是要动态创建柯里化的函数,余下的参数存储在 args 变量中。
执行 curry 函数返回的函数接收新的参数与 args 变量存储的参数合并,并把合并的参数传入给柯里化了的函数。
function multiFn(a, b, c) {
return a * b * c;
}
var multi = curry(multiFn);
multi(2,3,4);
复制代码结果:

虽然得到的结果是一样的,但是很容易发现存在问题,就是代码相对于之前的闭包实现方式较复杂,而且执行方式也不是题目要求的那样 multi(2)(3)(4)。那么下面就来改进这版代码。
改进版
就题目而言,是需要执行三次函数调用,那么针对柯里化后的函数,如果传入的参数没有 3 个的话,就继续执行 curry 函数接收参数,如果参数达到 3 个,就执行柯里化了的函数。
function curry(fn, args) {
var length = fn.length;
var args = args || [];
return function(){
newArgs = args.concat(Array.prototype.slice.call(arguments));
if(newArgs.length < length){
return curry.call(this,fn,newArgs);
}else{
return fn.apply(this,newArgs);
}
}
}
function multiFn(a, b, c) {
return a * b * c;
}
var multi = curry(multiFn);
multi(2)(3)(4);
multi(2,3,4);
multi(2)(3,4);
multi(2,3)(4);
复制代码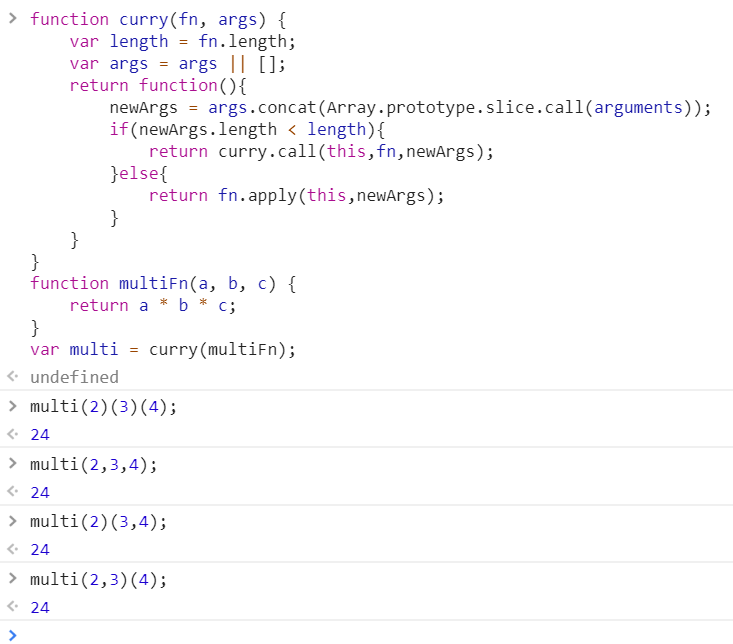
可以看到,通过改进版的柯里化函数,已经将题目定的实现方式扩展到好几种了。这种实现方案的代码扩展性就比较强了,但是还是有点不足,就是必须事先知道求值的参数个数,那能不能让代码更灵活点,达到随意传参的效果,例如: multi(2)(3)(4),multi(5)(6)(7)(8)(9) 这样的。
优化版
function multi() {
var args = Array.prototype.slice.call(arguments);
var fn = function() {
var newArgs = args.concat(Array.prototype.slice.call(arguments));
return multi.apply(this, newArgs);
}
fn.toString = function() {
return args.reduce(function(a, b) {
return a * b;
})
}
return fn;
}
复制代码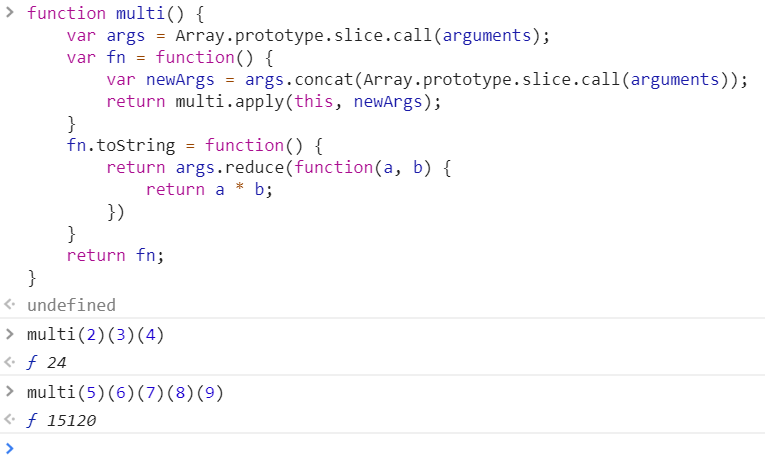
这样的解决方案就可以灵活的使用了。不足的是返回值是 Function 类型。

总结
- 就题目本身而言,是存在多种实现方式的,只要理解并充分利用闭包的强大。
- 可能在实际应用场景中,很少使用函数柯里化的解决方案,但是了解认识函数柯里化对自身的提升还是有帮助的。
- 理解闭包和函数柯里化之后,如果在面试中遇到类似的题型,应该就可以迎刃而解了。
后记
本着学习和总结的态度写的技术输出,文中有任何错误和问题,请大家指出。更多的技术输出可以查看我的 github博客。
整理了一些前端的学习资源,希望能够帮助到有需要的人,地址: 学习资源汇总。