循环神经网络RNN介绍1：什么是RNN、为什么需要RNN、前后向传播详解、Keras实现该文章的主要内容来自：Funda

该文章的主要内容来自：Fundamentals of Deep Learning – Introduction to Recurrent Neural Networks，笔者对该文章进行了翻译、注释、纠错、修改、公式编辑等，使文章更容易理解。

简介

让我们从一个问题开始，你能理解下面这句英文的意思吗？“working love learning we on deep”，答案显然是无法理解。那么下面这个句子呢？“We love working on deep learning”，整个句子的意思通顺了！我想说的是，一些简单的词序混乱就可以使整个句子不通顺。那么，我们能期待传统神经网络使语句变得通顺吗？不能！如果人类的大脑都感到困惑，我认为传统神经网络很难解决这类问题。

在日常生活中有许多这样的问题，当顺序被打乱时，它们会被完全打乱。例如，

我们之前看到的语言——单词的顺序定义了它们的意义
时间序列数据——时间定义了事件的发生
基因组序列数据——每个序列都有不同的含义

有很多这样的情况，序列的信息决定事件本身。如果我们试图使用这类数据得到有用的输出，就需要一个这样的网络：能够访问一些关于数据的先前知识（prior knowledge），以便完全理解这些数据。因此，循环神经网络（RNN）粉墨登场。

在这篇文章中，我假设读者了解神经网络的基本原理，如果你不知道的话，请在继续阅读之前先看知乎的相关文章，或者作者知乎专栏的相关文章。

我们需要一个用于处理序列的神经网络

在深入了解循环神经网络的细节之前，让我们考虑一下我们是否真的需要一个专门处理序列信息的网络。还有，我们可以使用这样的网络实现什么任务。

递归神经网络的优点在于其应用的多样性。当我们使用RNN时，它有强大的处理各种输入和输出类型的能力。看下面的例子。

情感分析(Sentiment Classification) – 这可以是简单的把一条推文分为正负两种情绪的任务。所以输入是任意长度的推文, 而输出是固定的长度和类型.

图像标注(Image Captioning) – 假设我们有一个图片，我们需要一个对该图片的文本描述。所以，我们的输入是单一的图像，输出是一系列或序列单词。这里的图像可能是固定大小的，但输出是不同长度的文字描述。

语言翻译(Language Translation) – 这里假设我们想将英文翻译为法语. 每种语言都有自己的语义，对同一句话有不同的长度。因此，这里的输入和输出是不同长度的。

因此，RNNs可用于将输入映射到不同类型、长度的输出，并根据实际应用泛化。让我们看看RNN的架构是怎样的。

什么是循环神经网络（RNN）

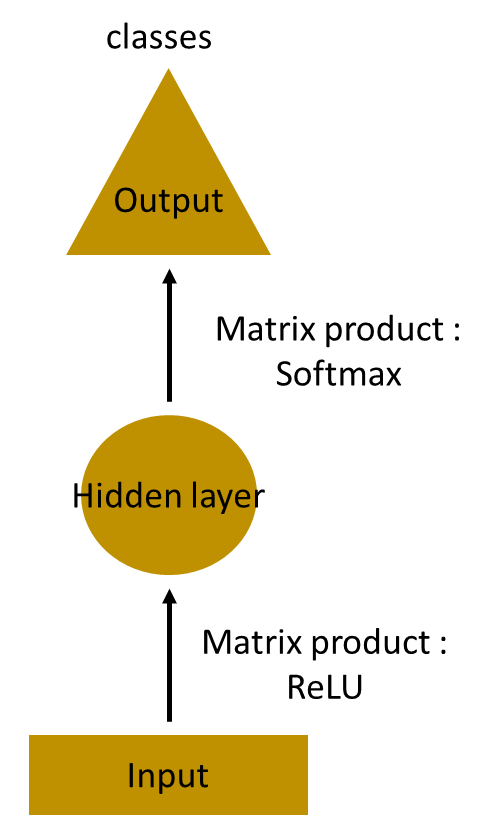
假设我们的任务是预测句子中的下一个词。让我们尝试使用MLP（多层感知机）完成它。先来看最简单的形式，我们有一个输入层、一个隐藏层和一个输出层。输入层接收输入，隐藏层激活，最后接收层得到输出。

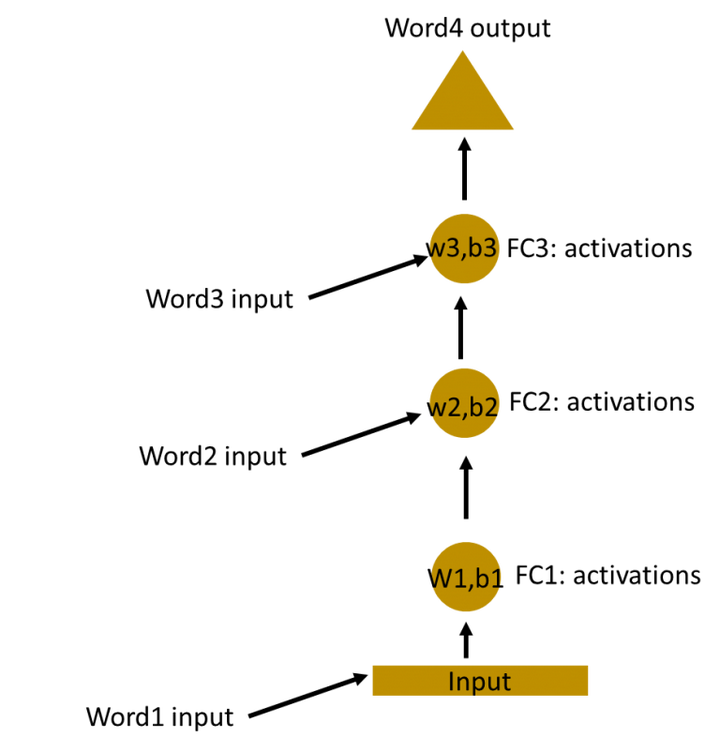
接下来搭建更深层的网络，其中有多个隐藏层。在这里，输入层接收输入，第一层隐藏层激活该输入，然后将这些激活发送到下一个隐藏层，并层层进行连续激活以得到输出。每个隐藏层有自己的权重和偏差。

由于每个隐藏层都有自己的权重和激活，所以它们具有独立的行为。现在的目标是确定连续输入之间的关系。我们能直接把输入给隐藏层吗？当然可以！

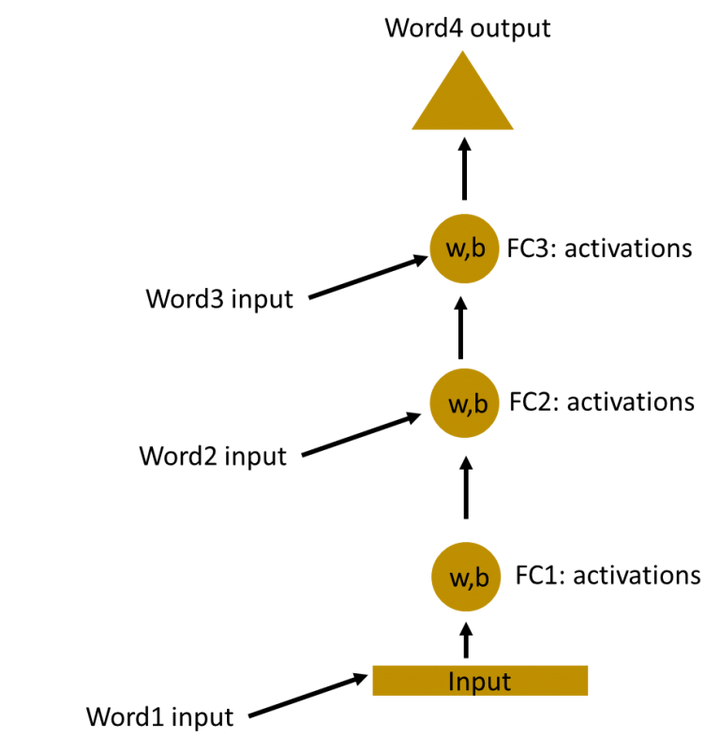
这些隐藏层的权重和偏差是不同的。因此，每一层都是独立的，不能结合在一起。为了将这些隐藏层结合在一起，我们使这些隐藏层具有相同的权重和偏差。

我们现在可以将这些隐藏层结合在一起，所有隐藏层的权重和偏差相同。所有这些隐藏层合并为一个循环层。

这就像将输入给隐藏层一样。在所有时间步（time steps）（后面会介绍什么是时间步），循环神经元的权重都是一样的，因为它现在是单个神经元。因此，一个循环神经元存储先前输入的状态，并与当前输入相结合，从而保持当前输入与先前输入的某些关系。

理解循环神经元（Recurrent Neuron）的细节

让我们先做一个简单的任务。让我们使用一个字符级别的RNN，在这里我们有一个单词“Hello”。所以我们提供了前4个字母h、e、l、l，然后让网络来预测最后一个字母，也就是“o”。所以这个任务的词汇表只有4个字母h、e、l、o。在涉及自然语言处理的实际情况中，词汇表一般会包括整个维基百科数据库中的单词，或一门语言中的所有单词。为了简单起见，这里，我们使用了非常小的词汇表。

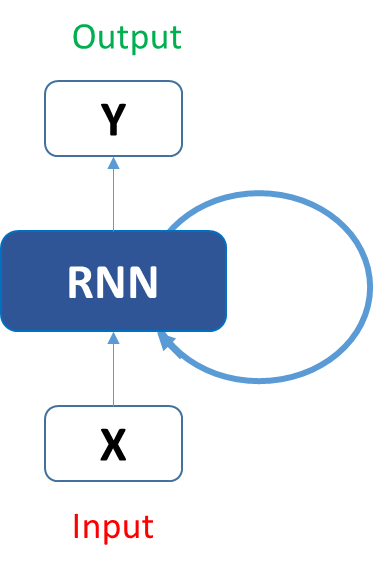
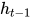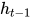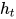让我们看看上面的结构是如何被用来预测“hello”这个单词的第五个字母的。在上面的结构中，蓝色RNN块，对输入和之前的状态应用了循环递归公式。在我们的任务中，字母“h”前面没有任何其他字母，我们来看字母“e”。当字母e被提供给网络时，将循环递归公式应用于输入（也就是字母e）和前一个状态（也就是字母h），得到新的状态。也就是说，在t-1的时候，输入是h，输出是 $h_{t-1}$ ,在t时刻，输入是e和 $h_{t-1}$ ，输出是 h_t ,这里每次应用循环递归公式称为不同的时间步。

描述当前状态的循环递归公式如下：

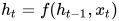
$h_t = f(h_{t-1},x_t)$

这里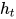 h_t 是t时刻的状态, 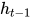$h_{t-1}$ 是前一时刻的状态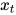， x_t 是当前的输入。我们有的是前一时刻的状态而不是前一时刻的输入, 因为输入神经元将前一时刻的输入转换为前一时刻的状态。所以每一个连续的输入被称为时间步。

在我们的案例中，我们有四个输入（h、e、l、l），在每一个时间步应用循环递推公式时，均使用相同的函数和相同的权重。

考虑循环神经网络的最简单形式，激活函数是tanh，权重是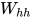 $W_{hh}$ ,输入神经元的权重是 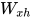$W_{xh}$ ,我们可以写出t时刻的状态公式如下

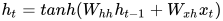
$h_t = tanh(W_{hh}h_{t-1}+W_{xh}x_{t})$

在上述情况下，循环神经元仅仅是将之前的状态考虑进去。对于较长的序列，方程可以包含多个这样的状态。一旦最终状态被计算出来我们就可以得到输出了。

现在，一旦得到了当前状态，我们可以计算输出了。

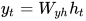
$y_t = W_{yh}h_t$

Ok，我们来总结一下循环神经元的计算步骤：

将输入时间步提供给网络，也就是提供给网络。
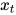接下来利用输入和前一时刻的状态计算当前状态，也就是
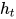
当前状态变成下一步的前一状态 $h_{t-1}$
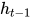
我们可以执行上面的步骤任意多次（主要取决于任务需要），然后组合从前面所有步骤中得到的信息。
一旦所有时间步都完成了，最后的状态用来计算输出
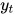
输出与真实标签进行比较并得到误差。
误差通过后向传播（后面将介绍如何后向传播）对权重进行升级，进而网络训练完成。

接下来，我们用Excel来计算一下这些状态，并得到输出。

用Excel实现循环神经元的前向传播

我们先来看看输入。

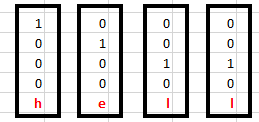
我们对输入进行one-hot编码。这是因为我们的整个词汇表只有四个字母{h,e,l,o}。

接下来我们将利用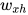 $w_{xh}$ 把输入转换为隐藏状态，这里我们采取随机的方式将权重初始化为3x4的矩阵。

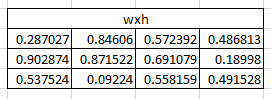
（注：这里矩阵的大小为什么是3x4？因为我们想计算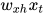 $w_{xh}x_t$ ,其中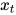是4x1的one-hot矩阵，根据矩阵乘法运算的法则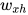， $w_{xh}$ 大小必须是nx4，n一般取比4小的值，因此 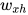$w_{xh}$ 的矩阵维度取3x4）

步骤1：

输入网络的第一个字母是“h”, 我们想要得到隐藏层状态，那么首先我们需要计算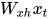 $W_{xh}x_t$ 。通过矩阵相乘，我们得到

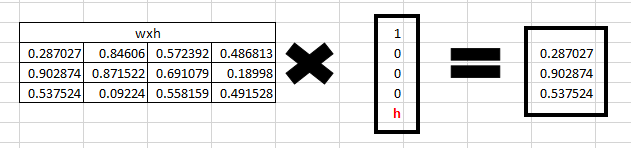
步骤2：

现在我们看一下循环神经元, 权重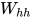 $W_{hh}$ 是一个1x1的矩阵，值为0.427043，偏差也是1x1的矩阵，值为0.56700.

对于字母“h”，没有前一个状态，所以我们也可以认为前一个状态是[0,0,0,0]。

接下来计算

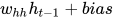
$w_{hh}h_{t-1}+bias$

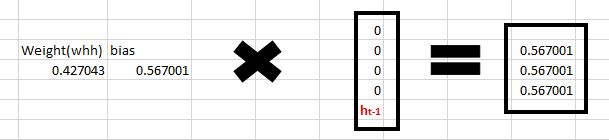
（译者注：读者一定注意到了，1x1的矩阵与一个4x1的矩阵相乘再加上一个1x1的矩阵，根据矩阵乘法的规则，是无法运算的。因此这里应该是使用了矩阵广播运算，而得到的结果应该是4x1的矩阵，而不是3x1的矩阵，但是被强制转换为了3x1的矩阵，原因是步骤1的输出结果是3x1的矩阵，接下来的步骤3将计算步骤1和步骤2的相加，所以步骤2的输出必须是3x1）

步骤3：

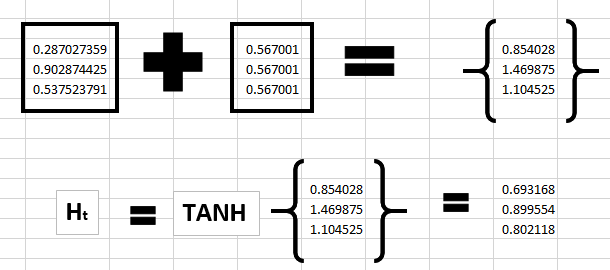
Ok，有了前两步，我们就可以计算当前循环神经元的状态了，根据以下公式

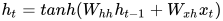
$h_t = tanh(W_{hh}h_{t-1}+W_{xh}x_{t})$

将前两步的结果代入公式即可得到当前步的状态，计算如下

步骤4：

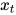现在我们继续关注下一个字母“e”被传入网络。上一步计算得到的 h_t 现在变成了这一步的 $h_{t-1}$ ,而e的one-hot向量是 x_t .现在我们来计算以下这一步的 h_t .

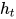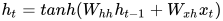
$h_t = tanh(W_{hh}h_{t-1}+W_{xh}x_{t})$

首先计算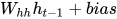 $W_{hh}h_{t-1} + bias$

再计算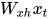 $W_{xh}x_t$

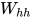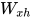（译者注：注意观察，计算上一步的状态与计算此步骤的状态使用的权重是一样的，也就是说使用的是同样的 $W_{hh}$ 和 $W_{xh}$ ，所以说循环神经元的特点是**权重共享）

步骤5：

有了步骤4的结果，代入公式可得输入字母“e”后的状态

同样，这一步得到的状态将变成下一步的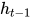 $h_{t-1}$ ，而循环神经元将使用这个状态和新输入字母来计算下一个状态.

步骤6：

在每一个状态，循环神经元还会计算输出. 现在我们来计算一下字母e的输出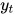 y_t .

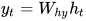
$y_t = W_{hy}h_t$

（译者注：注意，一个循环神经元根据输入和前一时间步的状态计算当前时间步的状态，然后根据当前时间步的状态计算输出。另外需要注意的是，这里的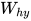 $W_{hy}$ 的维度大小是4x3，这是因为我们想得到4x1的输出，因为one-hot的维度是4x1，而通过下一步的计算每一个维度可以代表该维度的字母出现的概率）

步骤7：

通过应用softmax函数，我们可以得到词汇表中一个特定字母的出现的概率，所以我们现在计算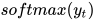 softmax(y_t)

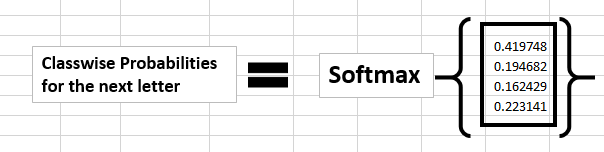
我们来理解一下得到的概率值。我们看到，这个模型认为字母e后面将出现的字母是h，因为概率最高的是代表字母h的那一维。可是实际上下一个字母应该是l，我们哪里做错了吗？并没有，只是我们还没有训练我们的网络。

好，我们面对的下一个大问题就是：RNN网络中如何实现后向传播？如何通过反馈循环来升级我们的权重？

循环神经网络的后向传播（BPTT）

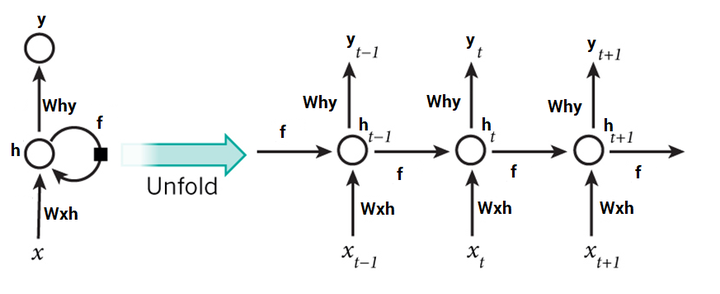
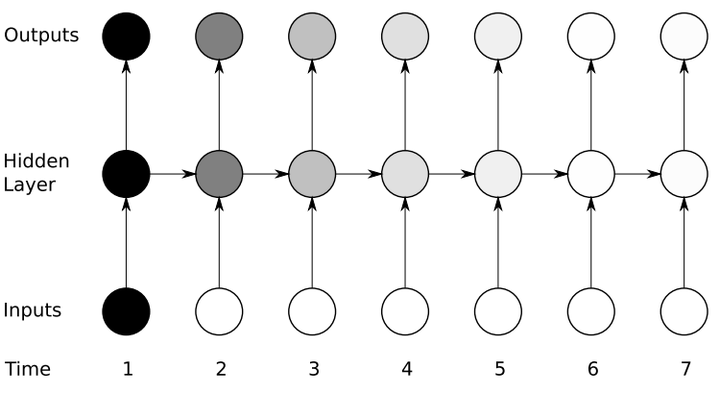
很难凭想象理解一个递归神经网络的权重是如何更新的。因此，为了理解和可视化反向传播，让我们按照时间步展开网络。在其中我们可以计算也可以不计算每一个时间步的输出。

在向前传播的情况下，输入随着每一个时间步前进。在反向传播的情况下，我们“回到过去”改变权重，因此我们叫它通过时间的反向传播（BPTT）。

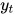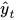如果 y_t 是预测值， $\hat y_t$ 是对应的实际值，那么，误差通过交叉熵损失来计算：

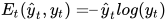
$E_t(\hat y_t,y_t) = – \hat y_t log(y_t)$

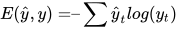
$E(\hat y,y) = – \sum \hat y_t log(y_t)$

我们通常把整个序列（单词）看作一个训练样本，所以总的误差是每个时间步（字符）中误差的和。权重在每一个时间步长是相同的（所以可以计算总误差后一起更新）。让我们总结一下反向传播的步骤。

首先使用预测输出和实际输出计算交叉熵误差
网络按照时间步完全展开
对于展开的网络，对于每一个实践步计算权重的梯度
因为对于所有时间步来说，权重都一样，所以对于所有的时间步，可以一起得到梯度（而不是像神经网络一样对不同的隐藏层得到不同的梯度）
随后对循环神经元的权重进行升级

展开的网络看起来像一个普通的神经网络。反向传播也类似于普通的神经网络，只不过我们一次得到所有时间步的梯度。我知道你在担心什么，现在如果有100个时间步，那么网络展开后将变得非常巨大（这是个挑战性的问题，我们后面讲介绍如何克服）。

如果你不想深入了解这背后的数学，所有你需要知道的是，按照时间步展开后的反向传播类似于常规神经网络的反向传播。我还将写一个有详细数学公式的关于循环神经网络的详细文章。

Keras部署循环神经网络

让我们使用循环神经网络来预测推文代表的情绪。我们希望将这些推文标记为正或负。你可以在这下载数据集。

我们有大约1600000条推文来训练我们的网络。如果你不熟悉自然语言处理的基础知识，我强烈建议你阅读这篇文章). 或者这篇关于词嵌入（word embedding）的详细文章。

下面让我们来使用RNN来将推文分为正类或负类。

# import all libraries

import keras

from keras.models import Sequential

from keras.layers import Dense, Activation, Dropout

from keras.layers.convolutional import Conv1D

from keras.preprocessing.text import Tokenizer

from keras.preprocessing.sequence import pad_sequences

import pandas as pd

import numpy as np

import spacy

nlp=spacy.load("en")

#load the dataset

train=pd.read_csv("../datasets/training.1600000.processed.noemoticon.csv" , encoding= "latin-1")

Y_train = train[train.columns[0]]

X_train = train[train.columns[5]]

# split the data into test and train

from sklearn.model_selection import train_test_split

trainset1x, trainset2x, trainset1y, trainset2y = train_test_split(X_train.values, Y_train.values, test_size=0.02,random_state=42 )

trainset2y=pd.get_dummies(trainset2y)

# function to remove stopwords

def stopwords(sentence):

   new=[]

   sentence=nlp(sentence)

    for w in sentence:

        if (w.is_stop == False) & (w.pos_ !="PUNCT"):

            new.append(w.string.strip())

        c=" ".join(str(x) for x in new)

    return c

# function to lemmatize the tweets

def lemmatize(sentence):

    sentence=nlp(sentence)

    str=""

    for w in sentence:

        str+=" "+w.lemma_

    return nlp(str)

#loading the glove model

def loadGloveModel(gloveFile):

    print("Loading Glove Model")

    f = open(gloveFile,'r')

    model = {}

    for line in f:

        splitLine = line.split()

        word = splitLine[0]

        embedding = [float(val) for val in splitLine[1:]]

        model[word] = embedding

    print ("Done."),len(model),(" words loaded!")

    return model

# save the glove model

model=loadGloveModel("/mnt/hdd/datasets/glove/glove.twitter.27B.200d.txt")

#vectorising the sentences

def sent_vectorizer(sent, model):

    sent_vec = np.zeros(200)

    numw = 0

    for w in sent.split():

        try:

            sent_vec = np.add(sent_vec, model[str(w)])

            numw+=1

        except:

            pass

    return sent_vec

#obtain a clean vector

cleanvector=[]

for i in range(trainset2x.shape[0]):

    document=trainset2x[i]

    document=document.lower()

    document=lemmatize(document)

    document=str(document)

    cleanvector.append(sent_vectorizer(document,model))

#Getting the input and output in proper shape

cleanvector=np.array(cleanvector)

cleanvector =cleanvector.reshape(32000,200,1)

#tokenizing the sequences

tokenizer = Tokenizer(num_words=16000)

tokenizer.fit_on_texts(trainset2x)

sequences = tokenizer.texts_to_sequences(trainset2x)

word_index = tokenizer.word_index

print('Found %s unique tokens.' % len(word_index))

data = pad_sequences(sequences, maxlen=15, padding="post")

print(data.shape)

#reshape the data and preparing to train

data=data.reshape(32000,15,1)

from sklearn.model_selection import train_test_split

trainx, validx, trainy, validy = train_test_split(data, trainset2y, test_size=0.3,random_state=42 )

#calculate the number of words

nb_words=len(tokenizer.word_index)+1

#obtain theembedding matrix

embedding_matrix = np.zeros((nb_words, 200))

for word, i in word_index.items():

    embedding_vector = model.get(word)

    if embedding_vector is not None:

        embedding_matrix[i] = embedding_vector

print('Null word embeddings: %d' % np.sum(np.sum(embedding_matrix, axis=1) == 0))

trainy=np.array(trainy)

validy=np.array(validy)

#building a simple RNN model

def modelbuild():

    model = Sequential()

    model.add(keras.layers.InputLayer(input_shape=(15,1)))

    keras.layers.embeddings.Embedding(nb_words, 15, weights=[embedding_matrix], input_length=15,

    trainable=False)



    model.add(keras.layers.recurrent.SimpleRNN(units = 100, activation='relu',

    use_bias=True))

    model.add(keras.layers.Dense(units=1000, input_dim = 2000, activation='sigmoid'))

    model.add(keras.layers.Dense(units=500, input_dim=1000, activation='relu'))

    model.add(keras.layers.Dense(units=2, input_dim=500,activation='softmax'))

    model.compile(loss='categorical_crossentropy', optimizer='adam', metrics=['accuracy']

    return model



#compiling the model

finalmodel = modelbuild()

finalmodel.fit(trainx, trainy, epochs=10, batch_size=120,validation_data=(validx,validy))

如果你运行上述模型，效果可能不是特别完美，因为这是一个非常简单的架构和相当浅的网络。我强烈建议读者自己调一调网络结构以取得更好的结果。另外，有多种方法可以对数据进行预处理。预处理将完全取决于手头的任务。

梯度爆炸和消失问题

RNN基于这样的机制，信息的结果依赖于前面的状态或前N个时间步。普通的RNN可能在学习长距离依赖性方面存在困难。例如，如果我们有这样一句话，“The man who ate my pizza has purple hair”。在这种情况下，purple hair描述的是The man，而不是pizza。所以这是一个长距离的依赖关系。

如果我们在这种情况下后向传播，我们就需要应用链式法则。在三个时间步后对第一个求梯度的公式如下：

∂E/∂W = ∂E/∂y3 ∂y3/∂h3 ∂h3/∂y2 *∂y2/∂h1 .. 这就是一个长距离的依赖关系.

在这里，我们应用了链式规则，如果任何一个梯度接近0，所有的梯度都会成指数倍的迅速变成零。这样将不再有助于网络学习任何东西。这就是所谓的消失梯度问题。

消失梯度问题与爆炸梯度问题相比，对网络更有威胁性，梯度爆炸就是由于单个或多个梯度值变得非常高，梯度变得非常大。

之所以我们更关心梯度消失问题，是因为通过一个预定义的阈值可以很容易地解决梯度爆炸问题。幸运的是，也有一些方法来处理消失梯度问题。如LSTM结构（长短期记忆网络）和GRU（门控性单位）可以用来处理消失的梯度问题。

其他RNN框架

当我们考虑长距离依赖性时，RNNs面临梯度消失问题。当参数的数量变得非常大时，它们也变得难以训练。如果我们展开网络，它变得如此巨大以至于如何收敛将是一个棘手的挑战。

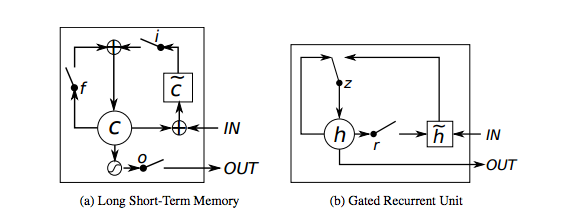
长短期记忆网络–通常被称为“LSTMs”–是一种特殊的RNN网络，能够学习长距离依赖性。由Hochreiter & Schmidhuber首先提出。他们在各种各样的问题上工作得非常出色，现在得到了广泛的应用。LSTMs也有这种链状结构，但重复的模块有一些稍微不同的结构。不是有一个单一的神经网络层，而是有多个层，以非常特殊的方式进行交互。它们有输入门、忘记门和输出门。我们将很快推出LSTMs的详细文章。

另一个有效的RNN网络架构是门控循环单元即GRUs。他们是LSTMs的变体，但是在结构上更简单，也更容易训练。它们的成功主要是由于门控网络信号控制当前输入和先前记忆如何使用，从而更新当前的激活并生成当前状态。这些门有自己的权重集，在学习阶段自适应地更新。我们这里只有两个门，重置门和更新门。敬请关注GRUs更详细的文章。

结束语

希望这篇文章能让你对循环神经网络有一个初步的了解。在以后的文章中我们将深入了解循环神经网络背后的数学，以及LSTMs和GRUs。试着使用这些RNNs并被他们的性能和应用所震撼。请在评论部分分享你的看法。

循环神经网络RNN介绍1：什么是RNN、为什么需要RNN、前后向传播详解、Keras实现

简介

目录

我们需要一个用于处理序列的神经网络

什么是循环神经网络（RNN）

理解循环神经元（Recurrent Neuron）的细节

用Excel实现循环神经元的前向传播

循环神经网络的后向传播（BPTT）

Keras部署循环神经网络

梯度爆炸和消失问题

其他RNN框架

结束语