算法思路
主要是基于基数排序,如果基数排序没弄懂代码就会很难理解:
- 首先从k=0开始,从后缀数组里面选取步长为2^k的后缀数组的前子串
- 然后进行基数排序
- 如果排序后所有的名次数组的值都不相同,那么排序结束;
- 否则,k++(也就是步长翻倍),继续排序。
几个概念
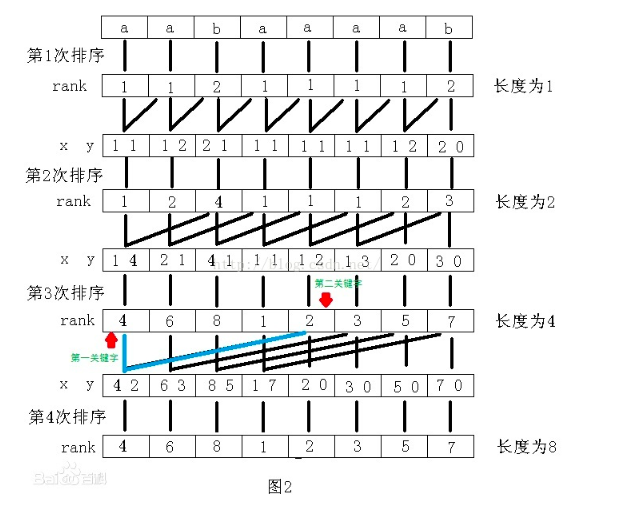
数组sa(sorted array):构造完成前表示关键字数组,下标表示名次,值表示关键字的首字符位置,值相同的时候名次根据在原串中相对位置的先后决定;构造完成后表示后缀数组,下标表示名次,值表示后缀的首字符位置。 比如'abb'的sa: sa[0] = 0 sa[1] = 2 sa[2] = 1
数组x:表示rank数组,下标表示关键字的位置,值表示关键字大小(rank),相同的值有相同的rank。初始化为字符串r的每个字符大小(此时x并不代表rank,只借助其值比较相对大小)。在每次迭代后,根据sa重新赋值,并代表rank。
数组y:排序后的第二关键字数组,下标表示名次,值代表第二关键字的首字符位置。也就是类似于第二关键字的sa数组。
for(i = 0; i < m; i++)
ws[i] = 0;
for(i = 0; i < n; i++)
ws[x[i] = r[i]]++;
for(i = 1; i < m; i++) //分为128个桶来进行基数排序
ws[i] += ws[i-1];
for(i = n-1; i >= 0; i--)
sa[--ws[x[i]]] = i;
上面代码的意思是,首先我们对数组初始化,m初始的时候我们简单采用ASICII码的m=128。要对长度为1的字符串进行排序,这样就求出了一个sa。
for(j=1,p=1;p<n;j*=2,m=p)
{
for(p=0,i=n-j;i<n;i++) y[p++]=i;
for(i=0;i<n;i++) if(sa[i]>=j) y[p++]=sa[i]-j;
for(i=0;i<n;i++) wv[i]=x[y[i]];
for(i=0;i<m;i++) ws[i]=0;
for(i=0;i<n;i++) ws[wv[i]]++;
for(i=1;i<m;i++) ws[i]+=ws[i-1];
for(i=n-1;i>=0;i--) sa[--ws[wv[i]]]=y[i];
for(t=x,x=y,y=t,p=1,x[sa[0]]=0,i=1;i<n;i++)
x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++;
}
这段代码非常精妙,也很难理解。 接下来我们从步长为1开始逐步倍增步长来进行基数排序,基数排序要分两次,第一次是对第二关键字排序,第二次是对第一关键字排序。对第二关键字排序的结果实际上可以利用上一次求得的sa直接算出,没有必要再算一次。那么怎么算呢?
-
首先是 for(p=0,i=n-j;i<n;i++) y[p++]=i; 这段的意思是下标i加上步长j如果超过了n,那么很明显第二关键字已经不存在了,那么越短的肯定要排在最前,同时我们按照原来的顺序排序保证算法的稳定。以长度为4时为例,下标超过4(图中rank为2)时的关键字将不存在第二关键字。
-
for(i=0;i<n;i++) if(sa[i]>=j) y[p++]=sa[i]-j; 这段的意思是,其余部分可以利用第一关键字的排序进行。但是第二关键字的下标和第一关键字的下标是不一样的,第一关键字的值对应下标就是该关键字的下标,第二关键字的值的下标减去j才是对应关键字的下标。举个例子,上面的第一个组合关键字是(4,2)下标为0。其中4是第一关键字下标0;2是第二关键字下标是4,需要减去长度4才能对应到组合关键字的下标。
-
wv[i] = x[y[i]];是最让人费解的。 这个的意思实际上是对后缀数组按照第二关键字重新排序得到一个新的后缀数组。这样的话后面我们再按照第一关键字排序后就是得到了合并以后的关键字顺序,它可以用于下次迭代。(仔细回想下基数排序,就是第一遍先分再收集,然后第二遍再分再收,不过基数排序的收集大多采用的复制的方式,而此时采用下标替换的方式,节省了内存)。
-
for(t = x,x = y,y = t,p = 1,x[sa[0]] = 0,i = 1; i < n;i++) x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++;
这一段也不好理解,目的呢是生成rank数组x。但是如果我们按照sa的方式简单映射,x[i]肯定是彼此不相同的。但是实际上当前步长下有可能他们的rank是相同的(图中的例子是不存在的,因为才排了一次rank就彼此不相同了)。 这里由于y数组实际上已经没用了,为了节省空间,我们交换x,y用y来保存rank值。
那么怎么判定重复? int cmp(int *r , int a, int b, int l) { return r[a] == r[b] && r[a+l] == r[b+l]; } 这段也需要仔细探讨下,我们直到最直接的办法是相邻的两个后缀数组从后缀数组的头一直比较到尾部,但是这里只比较了第一关键字和第二关键字对应的字符就可以了,这是为什么?因为我们直到假设当前步长是2^k,第一,二个关键字分别相当于前后2^(k-1)个字符的名次,名次如果都相同那整个字符串肯定都相同了.
并且,如果r[a]=r[b],说明以r[a]或r[b]开头的长度为l的字符串肯定不包括字符r[n-1](否则,那么他们的长度肯定不同,r[a],r[b]这两个名次必然不一样),所以调用变量r[a+l]和r[b+l]不会导致数组下标越界,这样就不需要做特殊判断。(这点也真的很妙)
还有两个细节,for(j=1,p=1;p<n;j=2,m=p) {…………}
- 在第一次排序以后,rank数组中的最大值小于p,所以让m=p。
- 变量p的结果实际上就是不同的字符串的个数。这里可以加一个小优化,如果p等于n,那么函数可以结束。因为在当前长度的字符串中,已经没有相同的字符串,接下来的排序不会改变rank值。例如图2中的第四次排序,实际上是没有必要的。
算法分析
每次基数排序是O(n),排序的次数决定于最长公共子串的长度,最坏情况需要循环logn次,所以总的复杂度为O(nlogn)。
空间上,引入了第二关键字排序数组y,rank数组x,计数器ws,中间数组wv。加上原本需要的r与sa以及对字串串数组转换成的int数组,一共是7n,空间要求为 O(n).
完整代码
#include<stdio.h>
#include<cstring>
#define maxn 100
int wa[maxn],wb[maxn],wv[maxn],ws[maxn];
int cmp(int *r , int a, int b, int l)
{
return r[a] == r[b] && r[a+l] == r[b+l];
}
void da (int *r , int *sa , int n, int m)
{
int i, j, p, *x = wa, *y = wb , *t;
for(i = 0; i < m; i++)
ws[i] = 0;
for(i = 0; i < n; i++)
ws[x[i] = r[i]]++;
for(i = 1; i < m; i++)
ws[i] += ws[i-1];
for(i = n-1; i >= 0; i--)
sa[--ws[x[i]]] = i;
for(j = 1,p = 1; p < n ; j <<= 1,m = p)
{
for(p = 0, i = n - j; i < n; i++)
y[p++]=i;
for(i = 0; i < n; i++)
if(sa[i] >= j)
y[p++] = sa[i] - j;
for(i = 0; i < n; i++)
wv[i] = x[y[i]]; //x相当于rank数组,最大值肯定是小于p的
for(i = 0; i < m; i++)
ws[i] = 0;
for(i = 0; i < n; i++)
ws[wv[i]]++;
for(i = 1; i < m; i++)
ws[i] += ws[i-1];
for(i = n-1; i >= 0; i--)
sa[--ws[wv[i]]] = y[i];
for(t = x,x = y,y = t,p = 1,x[sa[0]] = 0,i = 1; i < n;i++)
x[sa[i]]=cmp(y,sa[i-1],sa[i],j)?p-1:p++; //可以看出x[i]一定小于p
}
}
//测试代码
int main(){
const char r_str[] = "aadacabaababab";
int len = strlen(r_str);
int r[len];
int sa[len];
for(int i=0;i<len;r[i]=r_str[i],i++);
for(int i=0;i<len;i++){
printf("%d\n",r[i]);
}
da(r,sa,len,128);
for(int i=0;i<len;i++){
printf("%d\t%d\t",i,sa[i]);
for(int j=sa[i];j<len;j++)
printf("%c",r_str[j]);
printf("\n");
}
}