二分查找树BST的平衡问题

理想状况:插入、删除、查找时间代价为O(logn )
输入9,4,2,6,7,15,12,21
输入2,4, 6,7, 9, 12,15, 21
变成单链了

定义（red-black tree, 简称RB-tree）

红黑树:平衡的扩充二叉搜索树

颜色特征:结点是或“黑色”; “红色”
根特征 :根结点永远是“黑色”的;
外部特征:扩充外部叶结点都是空的“黑色”结点;
内部特征:“红色”结点的两个子结点都是“黑色”的，不允许两个连续的红色结点;
深度特征:任何结点到其子孙外部结点的每条简单路径都包含相同数目的“黑色”结点

红黑树的阶

结点X的阶(rank，也称“黑色高度”)

从该结点到外部结点的黑色结点数量，不包括 X 结点本身，包括叶结点
- 外部结点的阶是零
- 根的阶称为该树的阶

红黑树的性质

红黑树是满二叉树，空叶结点也看作结点
阶为 k 的红黑树路径长度最短是 k，最长是 2k （从根到叶的简单路径长度）
阶为 k 的红黑树树高最小是 k+1，最高是 2k+1
阶为 k 的红黑树的内部结点最少是一棵完全满二叉树，内部结点数最少是 2^k-1
n 个内部结点的红黑树树高,最大是 2log₂(n+1)+1

插入算法(参考这里的图示算法)

先调用 BST 的插入算法
- 把新记录着色为红色
- 若父结点是黑色，则算法结束
否则，双红调整
共分为四种情形
1. 新节点N位于树的根上，没有父节点。在这种情形下，我们把它重绘为黑色以满足性质2。
```
 void insert_case1(node *n){
 if(n->parent == NULL)
     n->color = BLACK;
 else
     insert_case2 (n);
 }
```
1. 新节点的父节点P是黑色，所以性质4没有失效（新节点是红色的）。直接插入，结束。
```
 void insert_case2(node *n){
 if(n->parent->color == BLACK)
     return; /* 树仍旧有效*/
 else
     insert_case3 (n);
}
```
1. 情形3:如果父节点P和叔父节点U二者都是红色，（此时新插入节点N做为P的左子节点或右子节点都属于情形3，这里右图仅显示N做为P左子的情形）则我们可以将它们两个重绘为黑色并重绘祖父节点G为红色（用来保持性质5）。现在我们的新节点N有了一个黑色的父节点P。因为通过父节点P或叔父节点U的任何路径都必定通过祖父节点G，在这些路径上的黑节点数目没有改变。但是，红色的祖父节点G可能是根节点，这就违反了性质2，也有可能祖父节点G的父节点是红色的，这就违反了性质4。为了解决这个问题，我们在祖父节点G上递归地进行情形1的整个过程。（把G当成是新加入的节点进行各种情形的检查）
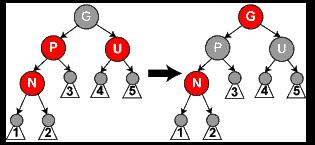
```
 void insert_case3(node *n){
 if(uncle(n) != NULL && uncle (n)->color == RED) {
     n->parent->color = BLACK;
     uncle (n)->color = BLACK;
     grandparent (n)->color = RED;
     insert_case1(grandparent(n));
 }
 else
     insert_case4 (n);
}
```
1. 情形4:父节点P是红色而叔父节点U是黑色或缺少，并且新节点N是其父节点P的右子节点而父节点P又是其父节点的左子节点。在这种情形下，我们进行一次左旋转调换新节点和其父节点的角色;接着，我们按情形5处理以前的父节点P以解决仍然失效的性质4。注意这个改变会导致某些路径通过它们以前不通过的新节点N（比如图中1号叶子节点）或不通过节点P（比如图中3号叶子节点），但由于这两个节点都是红色的，所以性质5仍有效。
```
 void insert_case4(node *n){
 if(n == n->parent->right && n->parent == grandparent(n)->left) {
     rotate_left(n->parent);
     n = n->left;
 } else if(n == n->parent->left && n->parent == grandparent(n)->right) {
     rotate_right(n->parent);
     n = n->right;
 }
 insert_case5 (p);
 }
```
1. 情形5：父节点P是红色而叔父节点U是黑色或缺少，新节点N是其父节点的左子节点，而父节点P又是其父节点G的左子节点。在这种情形下，我们进行针对祖父节点G的一次右旋转；在旋转产生的树中，以前的父节点P现在是新节点N和以前的祖父节点G的父节点。我们知道以前的祖父节点G是黑色，否则父节点P就不可能是红色（如果P和G都是红色就违反了性质4，所以G必须是黑色）。我们切换以前的父节点P和祖父节点G的颜色，结果的树满足性质4。性质5也仍然保持满足，因为通过这三个节点中任何一个的所有路径以前都通过祖父节点G，现在它们都通过以前的父节点P。在各自的情形下，这都是三个节点中唯一的黑色节点。

 void insert_case5(node *n){
     n->parent->color = BLACK;
     grandparent (n)->color = RED;
     if(n == n->parent->left && n->parent == grandparent(n)->left) {
         rotate_right(grandparent(n));
     } else {
         /* Here, n == n->parent->right && n->parent == grandparent (n)->right */
         rotate_left(grandparent(n));
     }
 }

删除算法

先调用 BST 的删除算法
- 待删除的结点有一个以上的外部空指针，则直接删除
- 否则在右子树中找到其后继结点进行值交换(着色不变)删除
v 是被删除的内结点, w 是被删外结点, X 是 w 的兄弟
- 如果v或者 X 是红色, 则把X标记为黑色即可
- 否则, X 需要标记为双黑, 根据其兄弟结点 C 进行重构调整

根据双黑 X 的兄弟 C 进行调整

假设X是左子结点(若X为右孩子，则对称)

情况 1: C 是黑色，且子结点有红色
- 重构，完成操作
情况 2:C 是黑色, 且有两个黑子结点
- 换色
- 父结点 B 原为黑色，可能需要从 B 继续向上调整
情况3:C是红色
- 转换状态
- C 转为父结点，调整为情况 1 或 2 继续处理

C++ 代码

#define BLACK 1
#define RED 0
#include <iostream>

using namespace std;

class bst {
private:

    struct Node {
        int value;
        bool color;
        Node *leftTree, *rightTree, *parent;

        Node() : value(0), color(RED), leftTree(NULL), rightTree(NULL), parent(NULL) { }        

        Node* grandparent() {
            if(parent == NULL){
                return NULL;
            }
            return parent->parent;
        }

        Node* uncle() {
            if(grandparent() == NULL) {
                return NULL;
            }
            if(parent == grandparent()->rightTree)
                return grandparent()->leftTree;
            else
                return grandparent()->rightTree;
        }

        Node* sibling() {
            if(parent->leftTree == this)
                return parent->rightTree;
            else
                return parent->leftTree;
        }
    };

    void rotate_right(Node *p){
        Node *gp = p->grandparent();
        Node *fa = p->parent;
        Node *y = p->rightTree;

        fa->leftTree = y;

        if(y != NIL)
            y->parent = fa;
        p->rightTree = fa;
        fa->parent = p;

        if(root == fa)
            root = p;
        p->parent = gp;

        if(gp != NULL){
            if(gp->leftTree == fa)
                gp->leftTree = p;
            else
                gp->rightTree = p;
        }

    }

    void rotate_left(Node *p){
        if(p->parent == NULL){
            root = p;
            return;
        }
        Node *gp = p->grandparent();
        Node *fa = p->parent;
        Node *y = p->leftTree;

        fa->rightTree = y;

        if(y != NIL)
            y->parent = fa;
        p->leftTree = fa;
        fa->parent = p;

        if(root == fa)
            root = p;
        p->parent = gp;

        if(gp != NULL){
            if(gp->leftTree == fa)
                gp->leftTree = p;
            else
                gp->rightTree = p;
        }
    }

    void inorder(Node *p){
        if(p == NIL)
            return;

        if(p->leftTree)
            inorder(p->leftTree);

        cout << p->value << " ";
                
        if(p->rightTree)
            inorder(p->rightTree);
    }

    string outputColor (bool color) {
        return color ? "BLACK" : "RED";
    }

    Node* getSmallestChild(Node *p){
        if(p->leftTree == NIL)
            return p;
        return getSmallestChild(p->leftTree);
    }

    bool delete_child(Node *p, int data){
        if(p->value > data){
            if(p->leftTree == NIL){
                return false;
            }
            return delete_child(p->leftTree, data);
        } else if(p->value < data){
            if(p->rightTree == NIL){
                return false;
            }
            return delete_child(p->rightTree, data);
        } else if(p->value == data){
            if(p->rightTree == NIL){
                delete_one_child (p);
                return true;
            }
            Node *smallest = getSmallestChild(p->rightTree);
            swap(p->value, smallest->value);
            delete_one_child (smallest);

            return true;
        }else{
           return false;
         }
    }

    void delete_one_child(Node *p){
        Node *child = p->leftTree == NIL ? p->rightTree : p->leftTree;
        if(p->parent == NULL && p->leftTree == NIL && p->rightTree == NIL){
            p = NULL;
            root = p;
            return;
        }
        
        if(p->parent == NULL){
            delete  p;
            child->parent = NULL;
            root = child;
            root->color = BLACK;
            return;
        }
        
        if(p->parent->leftTree == p){
            p->parent->leftTree = child;
        } else {
            p->parent->rightTree = child;
        }
        child->parent = p->parent;

        if(p->color == BLACK){
            if(child->color == RED){
                child->color = BLACK;
            } else
                delete_case (child);
        }

        delete p;
    }

    void delete_case(Node *p){
        if(p->parent == NULL){
            p->color = BLACK;
            return;
        }
        if(p->sibling()->color == RED) {
            p->parent->color = RED;
            p->sibling()->color = BLACK;
            if(p == p->parent->leftTree)
                rotate_left(p->sibling());
            else
                rotate_right(p->sibling());
        }
        if(p->parent->color == BLACK && p->sibling()->color == BLACK
                && p->sibling()->leftTree->color == BLACK && p->sibling()->rightTree->color == BLACK) {
            p->sibling()->color = RED;
            delete_case(p->parent);
        } else if(p->parent->color == RED && p->sibling()->color == BLACK
                && p->sibling()->leftTree->color == BLACK && p->sibling()->rightTree->color == BLACK) {
            p->sibling()->color = RED;
            p->parent->color = BLACK;
        } else {
            if(p->sibling()->color == BLACK) {
                if(p == p->parent->leftTree && p->sibling()->leftTree->color == RED
                        && p->sibling()->rightTree->color == BLACK) {
                    p->sibling()->color = RED;
                    p->sibling()->leftTree->color = BLACK;
                    rotate_right(p->sibling()->leftTree);
                } else if(p == p->parent->rightTree && p->sibling()->leftTree->color == BLACK
                        && p->sibling()->rightTree->color == RED) {
                    p->sibling()->color = RED;
                    p->sibling()->rightTree->color = BLACK;
                    rotate_left(p->sibling()->rightTree);
                }
            }
            p->sibling()->color = p->parent->color;
            p->parent->color = BLACK;
            if(p == p->parent->leftTree){
                p->sibling()->rightTree->color = BLACK;
                rotate_left(p->sibling());
            } else {
                p->sibling()->leftTree->color = BLACK;
                rotate_right(p->sibling());
            }
        }
    }

    void insert(Node *p, int data){
        if(p->value >= data){
            if(p->leftTree != NIL)
                insert(p->leftTree, data);
            else {
                Node *tmp = new Node();
                tmp->value = data;
                tmp->leftTree = tmp->rightTree = NIL;
                tmp->parent = p;
                p->leftTree = tmp;
                insert_case (tmp);
            }
        } else {
            if(p->rightTree != NIL)
                insert(p->rightTree, data);
            else {
                Node *tmp = new Node();
                tmp->value = data;
                tmp->leftTree = tmp->rightTree = NIL;
                tmp->parent = p;
                p->rightTree = tmp;
                insert_case (tmp);
            }
        }
    }

    void insert_case(Node *p){
        if(p->parent == NULL){
            root = p;
            p->color = BLACK;
            return;
        }
        if(p->parent->color == RED){
            if(p->uncle()->color == RED) {
                p->parent->color = p->uncle()->color = BLACK;
                p->grandparent()->color = RED;
                insert_case(p->grandparent());
            } else {
                if(p->parent->rightTree == p && p->grandparent()->leftTree == p->parent) {
                    rotate_left (p);
                    rotate_right (p);
                    p->color = BLACK;
                    p->leftTree->color = p->rightTree->color = RED;
                } else if(p->parent->leftTree == p && p->grandparent()->rightTree == p->parent) {
                    rotate_right (p);
                    rotate_left (p);
                    p->color = BLACK;
                    p->leftTree->color = p->rightTree->color = RED;
                } else if(p->parent->leftTree == p && p->grandparent()->leftTree == p->parent) {
                    p->parent->color = BLACK;
                    p->grandparent()->color = RED;
                    rotate_right(p->parent);
                } else if(p->parent->rightTree == p && p->grandparent()->rightTree == p->parent) {
                    p->parent->color = BLACK;
                    p->grandparent()->color = RED;
                    rotate_left(p->parent);
                }
            }
        }
    }

    void DeleteTree(Node *p){
        if(!p || p == NIL){
            return;
        }
        DeleteTree(p->leftTree);
        DeleteTree(p->rightTree);
        delete p;
    }
public:

    bst() {
        NIL = new Node();
        NIL->color = BLACK;
        root = NULL;
    }

    ~bst() {
        if (root)
            DeleteTree (root);
        delete NIL;
    }

    void inorder() {
        if(root == NULL)
            return;
        inorder (root);
        cout << endl;
    }

    void insert (int x) {
        if(root == NULL){
            root = new Node();
            root->color = BLACK;
            root->leftTree = root->rightTree = NIL;
            root->value = x;
        } else {
            insert(root, x);
        }
    }

    bool delete_value (int data) {
        return delete_child(root, data);
    }
private:
    Node *root, *NIL;
};

红黑树操作的代价

检索平均和最差时间都是O(log2 n)
- 自根向下查找
- 代价就是树高
插入、删除平均和最差时间都是O(log2 n)
- 先检索到待操作的位置
- 自底向根的方向调整，局部的调整操作
红黑树的持久版本对每次插入或删除需要是O(log2 n)的空间

应用场景

广泛用在C++的STL中。如map和set都是用红黑树实现的。适合小数据量，在内存中使用。

C++红黑树

二分查找树BST的平衡问题

定义（red-black tree, 简称RB-tree）

红黑树的阶

红黑树的性质

插入算法(参考这里的图示算法)

删除算法

根据双黑 X 的兄弟 C 进行调整

C++ 代码

红黑树操作的代价

应用场景