对数据结构进行记录,便于查看。
1. 算法复杂度
1.1 O表示的复杂度
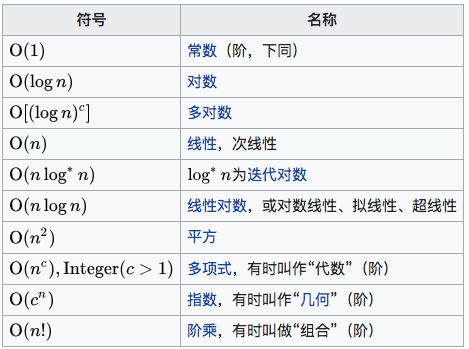
1.2 O(1)
赋值就是O(1)复杂度的,常数级的复杂度。
1.3 O(logn)
对数级别的算法复杂度,特点是数组数量越大时,增长的越缓慢。 在大量数据时性能较好
典型的是二分查找法:
function binarySearch(arr, target){
let start = 0;
let end = arr.length - 1;
while(start < end){
let mid = parseInt((start + end) / 2)
if(target < arr[mid]){
end = mid - 1;
}else if(target > arr[mid]){
start = mid + 1;
}else{
return mid;
}
}
return -1;
}
1.4 O(n)
典型的有顺序搜索算法。
function search(arr, targeet){
let index = -1;
for(let i = 0; i < arr.legth; i++){
if(arr[i] === target){
index = i;
}
}
return index;
}
1.5 O(n2)
平方级别的复杂度要尽量避免。 典型的有冒泡排序。
function bubbleSort(arr){
let len = arr.length;
for(let i = 0; i < len-1; i++){ //对前len-1个数都进行一边排序
for(let j = 0; j < len - 1 - i; j++){
if(arr[j] > arr[j+1]){
let temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
return arr;
}
2. 排序算法
2.1 快速排序
chrome中sort()函数默认用的是快速排序。
三步走:
- 从数组中取出一个数作为基数
- 分区,将数组分为两部分,比基数小的放在数组的左边,比基数大的放到数组的右边。
- 递归使左右区间重复第二步,直至各个区间只有一个数。
快速排序是分治策略的经典实现,分治的策略如下:
- 分解(Divide)步骤:将问题划分未一些子问题,子问题的形式与原问题一样,只是规模更小
- 解决(Conquer)步骤:递归地求解出子问题。如果子问题的规模足够小,则停止递归,直接求解
- 合并(Combine)步骤:将子问题的解组合成原问题的解
快速排序函数,我们需要将排序问题划分为一些子问题进行排序,然后通过递归求解,我们的终止条件就是,当array.length > 1不再生效时返回数组。
阮一峰版本的快排引起了很大的争议,主要是两方面:
- 取中间值不能用splice,直接用下标取值
- 用原地数组交换,不要每次循环都新建一个数组
时间复杂度O(nlogn),当数据有序时,以第一个关键字为基准分为两个子序列,前一个子序列为空,此时效率最低,所以数据越随机,性能越好,数据越接近有序,性能越差。 空间复杂度O(nlogn), 每次挖坑(找基准数)过程中需要一个空间存储基数,快排大概需要nlogn次的处理,所以空间也是nlogn。
快排中的切分方式
快排中最重要的步骤就是将小于等于中轴元素的整数放到中轴元素的左边,将大于中轴元素的数据放到中轴元素的右边,这里我们把该步骤定义为'切分'。以首元素作为中轴元素,下面介绍几种常见的'切分方式'。
1. 两端扫描,一端挖坑,一端填补
使用两个变量i和j,i指向最左边的元素,j指向最右边的元素,我们将首元素作为中轴,将首元素复制到变量pivot中,这时我们可以将首元素i所在的位置看成一个坑,我们从j的位置从右向左扫描,找一个小于等于中轴的元素A[j],来填补A[i]这个坑,填补完成后,拿去填坑的元素所在的位置j又可以看做一个坑,这时我们在以i的位置从前往后找一个大于中轴的元素来填补A[j]这个新的坑,如此往复,直到i和j相遇(i==j,此时i和j指向同一个坑)。最后我们将中轴元素放到这个坑中。最后对左半数组和右半数组重复上述操作。
2. 从两端扫描交换
使用两个变量i和j,i指向首元素的元素下一个元素(最左边的首元素为中轴元素),j指向最后一个元素,我们从前往后找,直到找到一个比中轴元素大的,然后从后往前找,直到找到一个比中轴元素小的,然后交换这两个元素,直到这两个变量交错(i > j)(注意不是相遇 i == j,因为相遇的元素还未和中轴元素比较)。最后对左半数组和右半数组重复上述操作。
function quick(arr,left,right){
if(left < right){//递归的边界条件,当 left === right时数组的元素个数为1个
let pivot = arr[left];//最左边的元素作为中轴
let i = left+1, j = right;
//当i == j时,i和j同时指向的元素还没有与中轴元素判断,
//小于等于中轴元素,i++,大于中轴元素j--,
//当循环结束时,一定有i = j+1, 且i指向的元素大于中轴,j指向的元素小于等于中轴
while(i <= j){
while(i <= j && arr[i] <= pivot){
i++;
}
while(i <= j && arr[j] > pivot){
j--;
}
//当 i > j 时整个切分过程就应该停止了,不能进行交换操作
//这个可以改成 i < j, 这里 i 永远不会等于j, 因为有上述两个循环的作用
if(i <= j){
swap(arr, i, j);
i++;
j--;
}
}
//当循环结束时,j指向的元素是最后一个(从左边算起)小于等于中轴的元素
swap(arr, left, j);//将中轴元素和j所指的元素互换
quick(arr, left, j-1);//递归左半部分
quick(arr, j+1, right);//递归右半部分
}
function quickSort(arr){
quick(arr,0,arr.length-1)
}
}
3. 从一端扫描
还是选最左边的数据为基准,arr[1,i]表示小于等于pivot的部分,i指向中轴元素,表示小于等于pivot的元素个数为0,j以后的都是未知元素,即不知道比pivot大,还是比中轴元素小。j初始化指向第一个未知元素。

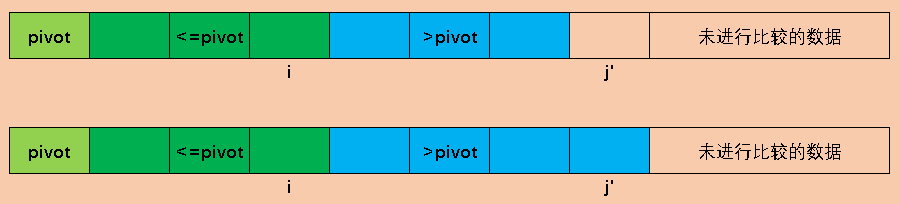
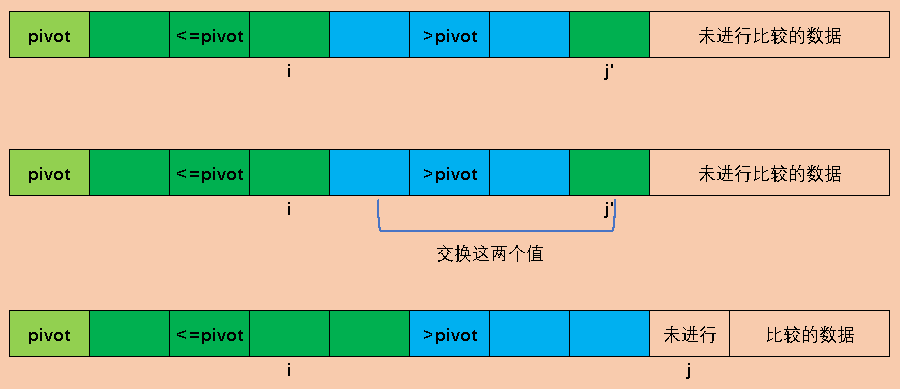
function quick(arr,left, right){
if(lift < right){
int pivot = arr[left];//最左边的元素作为中轴元素
//初始化时小于等于pivot的部分,元素个数为0
//大于pivot的部分,元素个数也为0
int i = left, j = left+1;
while(j <= right){
if(arr[j] <= pivot){
i++;
swap(arr, i, j);
j++;//j继续向前,扫描下一个
}else{
j++;//大于pivot的元素增加一个
}
}
//arr[i]及arr[i]以前的都小于等于pivot
//循环结束后arr[i+1]及它以后的都大于pivot
//所以交换arr[left]和arr[i],这样我们就将中轴元素放到了适当的位置
swap(arr, left, i);
quick(arr, left, i-1);
quick(arr, i+1, right);
}
}
function quickSort(arr){
quick(arr,0,arr.length-1)
}
快排中的优化
三向切分的快速排序
双轴快速排序
2.2 归并排序
归并排序的实现
firefox浏览器的sort()函数默认方法。 将两个已经排序的数组合并,要比将无序的数组合并快。 归并排序和快速排序都可以用构成二叉树来解释,只不过快排的复杂度花在了成树上(二叉搜索树,从上往下),归并的复杂度花在了归并上,
function mergeSort(arr){
let len = arr.length;
if(len<=1){
return arr;
}
let mid = Math.floor(len/2),
leftArr = arr.slice(0,mid),
rightArr = arr.slice(mid);
return merge(mergeSort(leftArr),mergeSort(rightArr))
}
//merge负责合并
function merge(leftArr, rightArr){
let result = [];
while(leftArr.length && rightArr.length){
if(leftArr[0]<=rightArr[0]){
result.push(leftArr.shift());
}else{
result.push(rightArr.shift());
}
}
while(leftArr.length){
result.push(leftArr.shift());
}
while(rightArr.length){
result.push(rightArr.shift());
}
return result;
}
栈溢出问题及解决
mergeSort会导致很频繁的自调用,一个长度为n的数组最终会调用2*(n-1)次mergeSort()。
如果需要排序的数组很长可能会在某些栈小的浏览器上发生溢出错误。
栈大小可以测试:
var cnt = 0;
try {
(function() {
cnt++;
arguments.callee();
})();
} catch(e) {
console.log(e.message, cnt);
}
遇到栈溢出错误并不一定要修改整个算法,只是表明递归不是最好的实现方式。这个合并排序算法同样可以迭代实现,比如(摘抄自《高性能JavaScript》):
function merge(left, right) {
var result = [];
while (left.length && right.length) {
if (left[0] < right[0])
result.push(left.shift());
else
result.push(right.shift());
}
return result.concat(left, right);
}
function mergeSort(a) {
if (a.length === 1)
return a;
var work = [];
for (var i = 0, len = a.length; i < len; i++)
work.push([a[i]]);
work.push([]); // 如果数组长度为奇数
for (var lim = len; lim > 1; lim = ~~((lim + 1) / 2)) {
for (var j = 0, k = 0; k < lim; j++, k += 2)
work[j] = merge(work[k], work[k + 1]);
work[j] = []; // 如果数组长度为奇数
}
return work[0];
}
console.log(mergeSort([1, 3, 4, 2, 5, 0, 8, 10, 4]));
这个版本的mergeSort()函数功能与前例相同却没有使用递归。尽管迭代版本的合并排序算法比递归实现要慢一些,但它并不会像递归版本那样受调用栈限制的影响。把递归算法改用迭代实现是实现栈溢出错误的方法之一。
2.3 冒泡排序和选择排序
都是O(N2)的复杂度。 冒泡前文有, 选择排序类似,也是对相邻进行两两比较,不同的是不是每比较一次就换位置,而是一轮比较完毕找到最大或最小值后放到正确的位置。
function selectionSort(arr){
let len=arr.length;
let minIndex,temp;
for(let i=0;i<len-1;i++){
minIndex=i;
for(var j=i+1;j<len;j++){
if(arr[j]<arr[minIndex]){ //寻找最小的数
minIndex=j; //将最小数的索引保存
}
}
temp=arr[i];
arr[i]=arr[minIndex];
arr[minIndex]=temp;
}
return arr;
3.其他算法
3.1 求二进制数中1的个数
任意给定一个32位无符号整数n,求n的二进制表示中1的个数,比如n = 5(0101)时,返回2,n = 15(1111)时,返回4
3.1.1普通法
function bitCount(n){
let count = 0;
while(n>0){
if((n&1)===1){
count++;
}
n = n >> 1;
}
return count;
}
function bitCount(n){
let count = 0;
for(count = 0; n; n=n>>1){
count += n&1;
}
return count;
}
3.1.2 快速法
速度较快,与n的大小无关,只与1的个数有关。 原理是n&(n-1)相当于清除最低位的1,从二进制的角度讲,n相当于在n-1的最低位加上1。
function bitCount(n){
let count = 0;
for(count = 0; n; count++){
n=n&(n-1)
}
return count;
}
3.1.3 制表法
3.1.3.1 动态建表
原理:根据奇偶性来分析,任一个正整数n,
- n是偶数,那么n的二进制中1的个数与n/2中1的个数是相同的,比如4和2的二进制中都有一个1,6和3的二进制中都有两个1。为啥?因为n是由n/2左移一位而来,而移位并不会增加1的个数。
- 如果n是奇数,那么n的二进制中1的个数是n/2中1的个数+1,比如7的二进制中有三个1,7/2 = 3的二进制中有两个1。为啥?因为当n是奇数时,n相当于n/2左移一位再加1。
再说一下查表的原理
对于任意一个32位无符号整数,将其分割为4部分,每部分8bit,对于这四个部分分别求出1的个数,再累加起来即可。而8bit对应2^8 = 256种01组合方式,这也是为什么表的大小为256的原因。
注意类型转换的时候,先取到n的地址,然后转换为unsigned char*,这样一个unsigned int(4 bytes)对应四个unsigned char(1bytes),分别取出来计算即可。举个例子吧,以87654321(十六进制)为例,先写成二进制形式-8bit一组,共四组,以不同颜色区分,这四组中1的个数分别为4,4,3,2,所以一共是13个1,如下面所示。
10000111 01100101 01000011 00100001 = 4 + 4 + 3 + 2 = 13
C++源码:
int BitCount(unsigned int n)
{
// 建表
unsigned char BitsSetTable256[256] = {0} ;
// 初始化表
for (int i =0; i <256; i++)
{
BitsSetTable256[i] = (i &1) + BitsSetTable256[i /2];
}
unsigned int c =0 ;
// 查表
unsigned char* p = (unsigned char*) &n ;
c = BitsSetTable256[p[0]] +
BitsSetTable256[p[1]] +
BitsSetTable256[p[2]] +
BitsSetTable256[p[3]];
return c ;
}
js:
function bitCount(n){
//建表
let bitsSetTable256 = [0];
//初始化表
for(let i=0;i<256;i++){
bitsSetTable256[i] = (i & 1) + bitsSetTable256[Math.floor(i/2)];
}
let count = 0;
count = bitsSetTable256[n & 0xff] + bitsSetTable256[(n>>8) & 0xff] + bitsSetTable256[(n>>8) & 0xff] + bitsSetTable256[(n>>8) & 0xff];
return count;
}
3.1.3.2 静态建表4bit
int BitCount(unsigned int n)
{
unsigned int table[16] =
{
0, 1, 1, 2,
1, 2, 2, 3,
1, 2, 2, 3,
2, 3, 3, 4
} ;
unsigned int count =0 ;
while (n)
{
count += table[n &0xf] ;
n >>=4 ;
}
return count ;
}
3.1.3.3 静态建表8bit
int BitCount(unsigned int n)
{
unsigned int table[256] =
{
0, 1, 1, 2, 1, 2, 2, 3, 1, 2, 2, 3, 2, 3, 3, 4,
1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5,
1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7,
1, 2, 2, 3, 2, 3, 3, 4, 2, 3, 3, 4, 3, 4, 4, 5,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7,
2, 3, 3, 4, 3, 4, 4, 5, 3, 4, 4, 5, 4, 5, 5, 6,
3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7,
3, 4, 4, 5, 4, 5, 5, 6, 4, 5, 5, 6, 5, 6, 6, 7,
4, 5, 5, 6, 5, 6, 6, 7, 5, 6, 6, 7, 6, 7, 7, 8,
};
return table[n &0xff] +
table[(n >>8) &0xff] +
table[(n >>16) &0xff] +
table[(n >>24) &0xff] ;
}
首先构造一个包含256个元素的表table,table[i]即i中1的个数,这里的i是[0-255]之间任意一个值。然后对于任意一个32bit无符号整数n,我们将其拆分成四个8bit,然后分别求出每个8bit中1的个数,再累加求和即可,这里用移位的方法,每次右移8位,并与0xff相与,取得最低位的8bit,累加后继续移位,如此往复,直到n为0。所以对于任意一个32位整数,需要查表4次。
第一次(n & 0xff) 10101011110011011110111100010010
第二次((n >> 8) & 0xff) 00000000101010111100110111101111
第三次((n >> 16) & 0xff)00000000000000001010101111001101
第四次((n >> 24) & 0xff)00000000000000000000000010101011
当然也可以建一个16bit的表,或者32bit,速度会更快。
3.1.4 平行算法
不一定是最快的, 将n写成二进制,然后相邻位增加,重复这个过程,直到只剩下一位。
function bitCount(n){
n = (n &0x55555555) + ((n >>1) &0x55555555) ;
n = (n &0x33333333) + ((n >>2) &0x33333333) ;
n = (n &0x0f0f0f0f) + ((n >>4) &0x0f0f0f0f) ;
n = (n &0x00ff00ff) + ((n >>8) &0x00ff00ff) ;
n = (n &0x0000ffff) + ((n >>16) &0x0000ffff) ;
return n ;
}
3.1.5 完美法
int BitCount(unsigned int n)
{
unsigned int tmp = n - ((n >>1) &033333333333) - ((n >>2) &011111111111);
return ((tmp + (tmp >>3)) &030707070707) %63;
}
第一行代码的作用
先说明一点,以0开头的是8进制数,以0x开头的是十六进制数,上面代码中使用了三个8进制数。
将n的二进制表示写出来,然后每3bit分成一组,求出每一组中1的个数,再表示成二进制的形式。比如n = 50,其二进制表示为110010,分组后是110和010,这两组中1的个数本别是2和3。2对应010,3对应011,所以第一行代码结束后,tmp = 010011,具体是怎么实现的呢?由于每组3bit,所以这3bit对应的十进制数都能表示为2^2 * a + 2^1 * b + c的形式,也就是4a + 2b + c的形式,这里a,b,c的值为0或1,如果为0表示对应的二进制位上是0,如果为1表示对应的二进制位上是1,所以a + b + c的值也就是4a + 2b + c的二进制数中1的个数了。举个例子,十进制数6(0110)= 4 * 1 + 2 * 1 + 0,这里a = 1, b = 1, c = 0, a + b + c = 2,所以6的二进制表示中有两个1。现在的问题是,如何得到a + b + c呢?注意位运算中,右移一位相当于除2,就利用这个性质!
4a + 2b + c 右移一位等于2a + b
4a + 2b + c 右移量位等于a
然后做减法
4a + 2b + c –(2a + b) – a = a + b + c,这就是第一行代码所作的事,明白了吧。
第二行代码的作用
在第一行的基础上,将tmp中相邻的两组中1的个数累加,由于累加到过程中有些组被重复加了一次,所以要舍弃这些多加的部分,这就是&030707070707的作用,又由于最终结果可能大于63,所以要取模。
需要注意的是,经过第一行代码后,从右侧起,每相邻的3bit只有四种可能,即000, 001, 010, 011,为啥呢?因为每3bit中1的个数最多为3。所以下面的加法中不存在进位的问题,因为3 + 3 = 6,不足8,不会产生进位。
tmp + (tmp >> 3)-这句就是是相邻组相加,注意会产生重复相加的部分,比如tmp = 659 = 001 010 010 011时,tmp >> 3 = 000 001 010 010,相加得
001 010 010 011
000 001 010 010
001 011 100 101
011 + 101 = 3 + 5 = 8。(感谢网友Di哈指正。)注意,659只是个中间变量,这个结果不代表659这个数的二进制形式中有8个1。
注意我们想要的只是第二组和最后一组(绿色部分),而第一组和第三组(红色部分)属于重复相加的部分,要消除掉,这就是&030707070707所完成的任务(每隔三位删除三位),最后为什么还要%63呢?因为上面相当于每次计算相连的6bit中1的个数,最多是111111 = 77(八进制)= 63(十进制),所以最后要对63取模。