【刷算法】判断链表是否有环以及返回入环节点

题目描述

判断一个单链表是否有环，有环则返回入环节点，否则返回null

1->2->3->4->5->6
            ↑  ↓
            8<-7

例如上面这个链表就有环，入环节点是5

判断链表有环

通常判断链表是否有环，会采用快慢指针的方法，其实道理很简单，就像两个人赛跑且一个人跑得快一个人跑得慢。如果赛道是直的，那么快人跑到终点时慢人还未到；如果赛道是环形，则快人和慢人总会相遇。
代码实现

    function ListNode(x){
        this.val = x;
        this.next = null;
    }
    function EntryNodeOfLoop(pHead){
    if(pHead === null)
        return null;
    // 快慢指针从链表的头部开始
    var fast = pHead;
    var slow = pHead;
    
    while(slow.next !==null && fast.next.next !== null) {
    // 快指针每次走两步；慢指针每次走一步
        slow = slow.next;
        fast = fast.next.next;
        // 快慢指针相遇时，跳出while循环
        if(slow === fast)
            break;
    }
    // 快指针已经到了链表尾部了还没和慢指针相遇，说明没有环
    if(fast === null || fast.next === null)
        return null;
        
    // 后续会处理有环的情况...
    }

找到入环节点

常见的方法是：在确定链表有环之后，慢指针重新指向链表头，快指针留在相遇处；然后快慢指针再以每次移动1个节点的速度前进，最终他们在入环节点相遇。 为什么这么做就可以保证在入环节点相遇？证明一下：

如图，设整个链表长度为L，环长度为R，且距离具有方向性，例如CB是C点到B点的距离，BC是B点到C点的距离，CB!=BC。当证明有环时，fast和slow都顺时针到了B点，则此时：

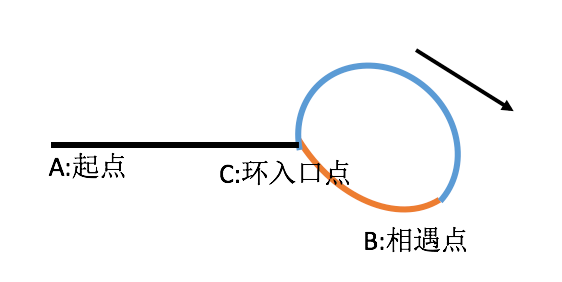
slow走的距离：AC+CB
fast走的距离：AC+k*R+CB(k=0,1,2...)

由于fast每次走2个节点，slow每次走1个节点，所以：

2(AC+CB) = AC+k*R+CB
AC+CB = k*R
AC+CB = (k-1)*R+R
AC = (k-1)*R+R-CB
AC = (k-1)*R+BC

从最终的表达式可以看出来，AC的距离等于绕环若干圈后再加上BC的距离，也就是说慢指针从A点出发以速度1前进、快指针从B点出发以速度1前进，则慢指针到C点时，快指针也必然到了。 代码实现：

    function ListNode(x){
        this.val = x;
        this.next = null;
    }
    function EntryNodeOfLoop(pHead){
        if(pHead === null)
            return null;
        var fast = pHead;
        var slow = pHead;
    
        while(slow.next !==null && fast.next.next !== null) {
            slow = slow.next;
            fast = fast.next.next;
            if(slow === fast)
                break;
        }
    
        if(fast === null || fast.next === null)
            return null;
        // 有环，slow重新回到链表头
        slow = pHead;
        
        // slow和fast重新相遇时，相遇节点就是入环节点
        while(slow !== fast) {
            slow = slow.next;
            fast = fast.next;
        }
    
        return slow;
    }