思想:对于最新发现的顶点v,如果它还有以此为起点而还未探索的边,沿此边探索。如果v的所有边已经探索完了,再回溯到发现v有起始点的那些边。一直到已经探索了从源起点可到的所有顶点为止。如果还有没探索的顶点,将它定义为一个新的源顶点,继续上述过程。
像走迷宫一样,尝试每种可能的结果,没走通,就回溯到当初分叉的路口,继续探索
探索整个的图
DFS(V,Adj):
parent={}
for s in V: //遍历图中所有的点
if s not in parent: //点没有遍历过就继续探索
parent[s]=None //源点不设置父节点
DFS-Visit(Adj,s) //探索当前源顶点能够到达的所有的点
给定一个源顶点s,DFS的实现方式
DFS-Visit(Adj,s):
for v in Adj[s]: //遍历所有的边
if v not in parent: //当前边没有遍历过
parent[v]=s //记录已经遍历
DFS-Visit(adj,v) //优先探索当前节点的边,完成之后,再执行回溯(通过循环实现)
以有向图为例
假设按照字母的顺序来遍历所有的顶点,即V=[a,b,c,d,e,f],原始的图为
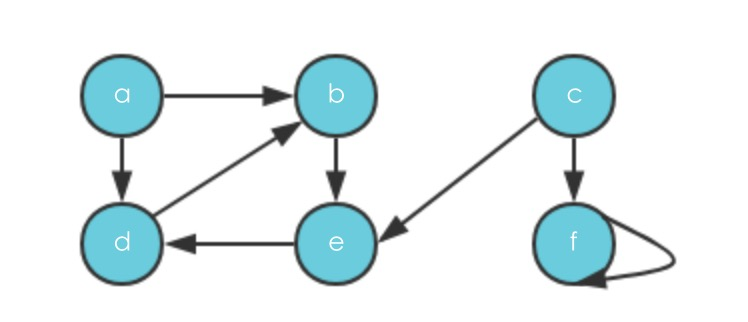
- 第一步探索a到b的边,发现b还有边,一直往下走,直到d为止,d没有往下走的边,第一个DFS-Visit执行结束
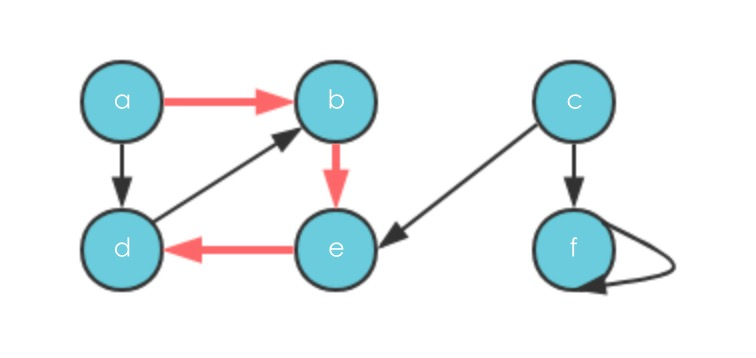
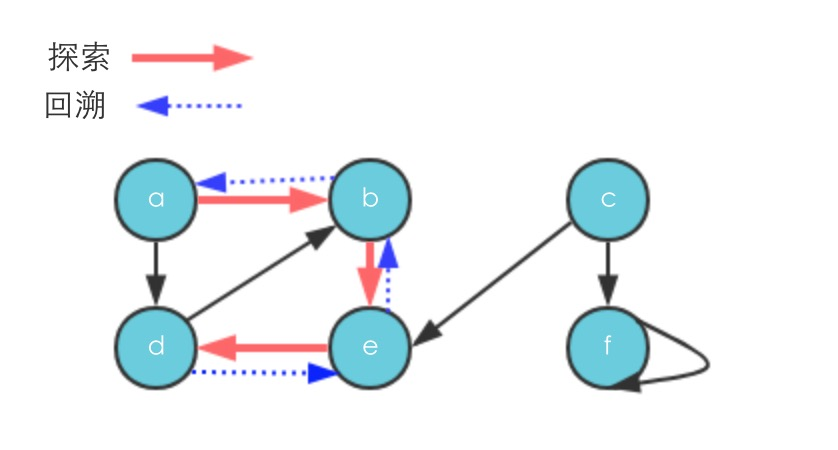
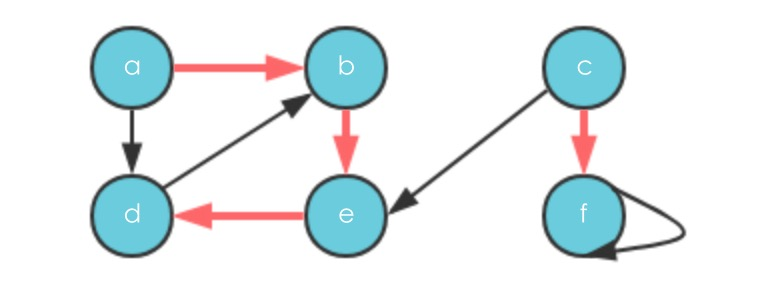
- 继续更换源点一直到f,都没有新的尚未探索过的边,最终DFS探索生成了两颗深度优先树
深度优先树指的是经过DFS生成的树,结果为3中的橙色箭头所指的两个部分
时间复杂度
O(V+E);它的遍历规则仍然需要遍历所有的节点一遍,对于每条变来讲,只有没有遍历过的才做一次遍历
深度优先搜索的用途是什么?
1. 边分类
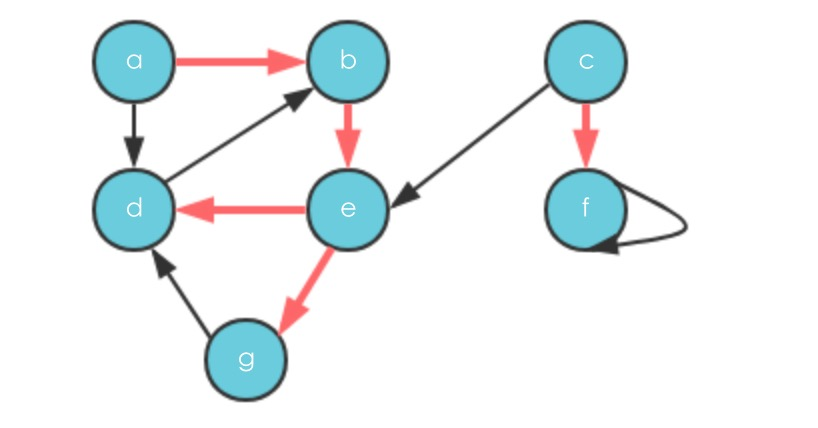
- 树边。如果顶点v是在探寻边(u,v)首次发现的,那么(u,v)是树边,比如图中(a,b)
- 正向边。u到v的某个非树边,比如图中(a,d),a到d存在边,但是没有进入树中
- 反边。 连接u到它的祖先顶点v的边,比如图中的(d,b)
- 交叉边。生成的树中,两个顶点不存在父子关系。比如图中的 (g,d)
在算法中,树边判断通过parent就可以看出,parent的逆向就是树边,得以标识;
反边判断,可以在源点开始做一个标记,把所有的经过的节点都放入栈中,如果下次得到的顶点在栈中,那么这条边就是反边;
如何判断在一个图中是否存在环?
图G存在环,当且仅当图中存在一条反边。证明如下:
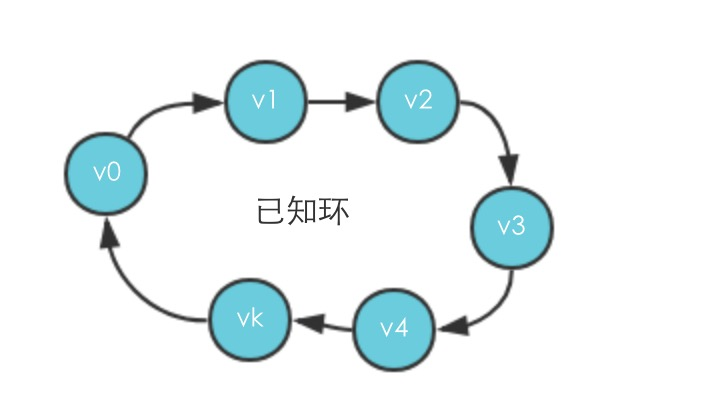
- 存在环,证明有反边。假设从环中选取一个点
,作为DFS遍历的第一个顶点,证明 (
,
)是反边:已知事实是,
访问前,
必定已经访问完,
访问前,
必定已经访问完,当访问到
再下一个查看
的时候,
已经在栈中,那么(
,
)是反边
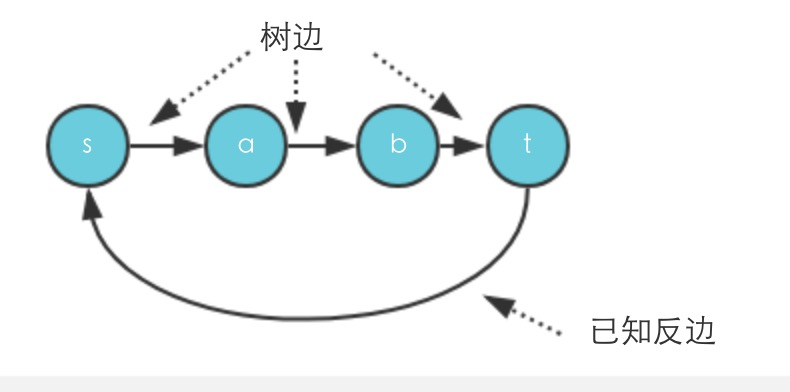
- 存在反边,证明有环。首先s到t必然存在树边,然后t到s是一条反边,那必然成环
2. Job调度
Job本身是个无环的有向图,各个顶点之间必定存在着一定的顺序,执行的时候等前面的执行完才能再执行排在后面的
它使用的算法称作拓扑排序,拓扑排序内部使用的就是DFS,输出为完成时的顶点的逆序,就排序好了(之前记录的是parent的指向,真正的执行是先parent)
这种排序产生的结果是,假设图中所有的顶点放在同一个水平线上,那么所有的方向均是从左到右
证明
只需要证明,对于任何一个边e=(u,v),在v执行完之后,u才执行完
- u的访问发生在v之前:由于u,v之间存在一条边,那么在u执行完之前,肯定为访问v,而等v完成后,才能完成u
- v的访问在u之前:由于u和v之间存在一条边,如果先访问了v,如果存在v到u的路径,这样会有环,所以根本不会执行u,也就是说,v先执行完
附录
算法导论(MIT 6.006 第14讲)