对于一般的分布的采样，在很多的编程语言中都有实现，如最基本的满足均匀分布的随机数，但是对于复杂的分布，要想对其采样，却没有实现好的函数，在这里，可以使用马尔可夫链蒙特卡罗(Markov Chain Monte Carlo, MCMC)方法，其中Metropolis-Hastings采样和Gibbs采样是MCMC中使用较为广泛的两种形式。

MCMC的基础理论为马尔可夫过程，在MCMC算法中，为了在一个指定的分布上采样，根据马尔可夫过程，首先从任一状态出发，模拟马尔可夫过程，不断进行状态转移，最终收敛到平稳分布。

一、马尔可夫链

1、马尔可夫链

设 $X_t$ 表示随机变量 $X$ 在离散时间 $t$ 时刻的取值。若该变量随时间变化的转移概率仅仅依赖于它的当前取值，即

P( Xt +1 =s j ∣X 0 =s 0 ,X 1 =s 1 ,⋯ ,Xt=s i ) =P( Xt +1 =s j ∣X t =s i ) P (X t +1 =s j ∣X 0 =s 0 ,X 1 =s 1 ,⋯, X t = s i ) = P ( X t +1 = s j ∣ X t = s i )

也就是说状态转移的概率只依赖于前一个状态。称这个变量为马尔可夫变量，其中， $s_0,s_1,\cdots ,s_i,s_j\in \Omega$ 为随机变量 $X$ 可能的状态。这个性质称为马尔可夫性质，具有马尔可夫性质的随机过程称为马尔可夫过程。

马尔可夫链指的是在一段时间内随机变量 $X$ 的取值序列 $\left ( X_0,X_1,\cdots ,X_m \right )$ ，它们满足如上的马尔可夫性质。

2、转移概率

马尔可夫链是通过对应的转移概率定义的，转移概率指的是随机变量从一个时刻到下一个时刻，从状态 $s_i$ 转移到另一个状态 $s_j$ 的概率，即：

P ( i→j) := Pi ,j =P ( Xt +1 =s j ∣ X t =s i )

记 $\pi _k^{\left ( t \right )}$ 表示随机变量 $X$ 在时刻 $t$ 的取值为 $s_k$ 的概率，则随机变量 $X$ 在时刻 $t+1$ 的取值为 $s_i$ 的概率为：

π ( t+1) i = P( Xt +1 = s i ) = ∑ k P( X t + 1 = s i ∣ X t = s k ) ⋅ P( X t = s k ) = ∑ k P k ,i ⋅ π ( t) k

假设状态的数目为 $n$ ，则有：

( π( t+1) 1 ,⋯ ,π ( t+1) n ) =( π( t) 1 ,⋯ ,π ( t) n ) [ P 1, 1 P 1, 2 ⋯ P 1,n P 2, 1 P 2, 2 ⋯ P 2,n ⋮ ⋮ ⋮ P n ,1 P n ,2 ⋯ P n ,n ]

3、马尔可夫链的平稳分布

对于马尔可夫链，需要注意以下的两点：

1、周期性：即经过有限次的状态转移，又回到了自身；
2、不可约：即两个状态之间相互转移；

如果一个马尔可夫过程既没有周期性，又不可约，则称为各态遍历的。

对于一个各态遍历的马尔可夫过程，无论初始值 $\pi ^{\left ( 0 \right )}$ 取何值，随着转移次数的增多，随机变量的取值分布最终都会收敛到唯一的平稳分布 $\pi ^{\ast }$ ，即：

l imt →∞ π (0 ) P t =π ∗

且这个平稳分布 $\pi ^{\ast }$ 满足：

π ∗ P =π ∗

其中， $\mathbf{P}=\left ( p_{i,j} \right )_{n\times n}$ 为转移概率矩阵。

二、马尔可夫链蒙特卡罗方法

1、基本思想

对于一个给定的概率分布 $P\left (X \right )$ ，若是要得到其样本，通过上述的马尔可夫链的概念，我们可以构造一个转移矩阵为 $\mathbf{P}$ 的马尔可夫链，使得该马尔可夫链的平稳分布为 $P\left (X \right )$ ，这样，无论其初始状态为何值，假设记为 $x_0$ ，那么随着马尔科夫过程的转移，得到了一系列的状态值，如： $x_0,x_1,x_2,\cdots ,x_n,x_{n+1},\cdots ,$ ，如果这个马尔可夫过程在第 $n$ 步时已经收敛，那么分布 $P\left (X \right )$ 的样本即为 $x_n,x_{n+1},\cdots$ 。

2、细致平稳条件

对于一个各态遍历的马尔可夫过程，若其转移矩阵为 $\mathbf{P}$ ，分布为 $\pi \left ( x \right )$ ，若满足：

π ( i) P i , j = π( j) P j ,i

则 $\pi \left ( x \right )$ 是马尔可夫链的平稳分布，上式称为细致平稳条件。

3、Metropolis采样算法

Metropolis采样算法是最基本的基于MCMC的采样算法。

3.1、Metropolis采样算法的基本原理

假设需要从目标概率密度函数 $p\left ( \theta \right )$ 中进行采样，同时， $\theta$ 满足 $-\infty <\theta <\infty$ 。Metropolis采样算法根据马尔可夫链去生成一个序列：

θ ( 1) → θ ( 2 ) → ⋯θ ( t) →

其中， $\theta ^{\left (t \right )}$ 表示的是马尔可夫链在第 $t$ 代时的状态。

在Metropolis采样算法的过程中，首先初始化状态值 $\theta ^{\left (1 \right )}$ ，然后利用一个已知的分布 $q\left ( \theta \mid \theta ^{\left ( t-1 \right )} \right )$ 生成一个新的候选状态 $\theta ^{\left (\ast \right )}$ ，随后根据一定的概率选择接受这个新值，或者拒绝这个新值，在Metropolis采样算法中，概率为：

α = mi n( 1, p ( θ ( ∗) ) p ( θ ( t−1 ) ) )

这样的过程一直持续到采样过程的收敛，当收敛以后，样本 $\theta ^{\left (t \right )}$ 即为目标分布 $p\left ( \theta \right )$ 中的样本。

3.2、Metropolis采样算法的流程

基于以上的分析，可以总结出如下的Metropolis采样算法的流程：

初始化时间 $t=1$
设置 $u$ 的值，并初始化初始状态 $\theta ^{\left (t \right )}=u$
重复一下的过程：
- 令 $t=t+1$
- 从已知分布 $q\left ( \theta \mid \theta ^{\left ( t-1 \right )} \right )$ 中生成一个候选状态 $\theta ^{\left (\ast \right )}$
- 计算接受的概率： $\alpha =min\: \left ( 1,\; \frac{p\left ( \theta ^{\left ( \ast \right )} \right )}{p\left ( \theta ^{\left ( t-1 \right )} \right )} \right )$
- 从均匀分布 $Uniform\left ( 0, 1 \right )$ 生成一个随机值 $a$
- 如果 $a\leqslant \alpha$ ，接受新生成的值： $\theta ^{\left (t \right )}=\theta ^{\left (\ast \right )}$ ；否则： $\theta ^{\left (t \right )}=\theta ^{\left (t-1 \right )}$
直到 $t=T$

3.3、Metropolis算法的解释

要证明Metropolis采样算法的正确性，最重要的是要证明构造的马尔可夫过程满足如上的细致平稳条件，即：

π ( i) P i ,j = π( j) P j ,i

对于上面所述的过程，分布为 $p\left ( \theta \right )$ ，从状态 $i$ 转移到状态 $j$ 的转移概率为：

P i ,j = α i ,j ⋅ Q i ,j

其中， $Q_{i,j}$ 为上述已知的分布。

对于选择该已知的分布，在Metropolis采样算法中，要求该已知的分布必须是对称的，即 $Q_{i,j}=Q_{j,i}$ ，即

q ( θ= θ ( t) ∣ θ ( t− 1 ) ) = q( θ =θ ( t − 1 ) ∣ θ ( t ) )
常用的符合对称的分布主要有：正态分布，柯西分布以及均匀分布等。

接下来，需要证明在Metropolis采样算法中构造的马尔可夫链满足细致平稳条件。

p ( θ( i) ) Pi ,j = p( θ( i) ) ⋅α i,j ⋅Q i,j =p( θ( i) ) ⋅m i n { 1,p ( θ( j) ) p ( θ( i) ) } ⋅Q i,j = min { p( θ( i) ) Q i , j , p( θ ( j) ) Q i ,j } = p( θ ( j) ) ⋅ mi n { p ( θ ( i) ) p ( θ ( j) ) , 1} ⋅ Q j , i = p ( θ ( j ) ) ⋅ α j , i ⋅ Q j , i = p ( θ ( j ) ) P j , i

因此，通过以上的方法构造出来的马尔可夫链是满足细致平稳条件的。

3.4、实验

假设需要从柯西分布中采样数据，我们利用Metropolis采样算法来生成样本，其中，柯西分布的概率密度函数为：

f( θ)=1π ( 1 +θ 2 )

那么，根据上述的Metropolis采样算法的流程，接受概率 $\alpha$ 的值为：

α= mi n ( 1,1 +[ θ( t ) ] 2 1 +[ θ( ∗ ) ] 2 )

代码如下：

'''
Date:20160629
@author: zhaozhiyong
'''
import random
from scipy.stats import norm
import matplotlib.pyplot as plt

def cauchy(theta):
    y = 1.0 / (1.0 + theta ** 2)
    return y

T = 5000
sigma = 1
thetamin = -30
thetamax = 30
theta = [0.0] * (T+1)
theta[0] = random.uniform(thetamin, thetamax)

t = 0
while t < T:
    t = t + 1
    theta_star = norm.rvs(loc=theta[t - 1], scale=sigma, size=1, random_state=None)
    #print theta_star
    alpha = min(1, (cauchy(theta_star[0]) / cauchy(theta[t - 1])))

    u = random.uniform(0, 1)
    if u <= alpha:
        theta[t] = theta_star[0]
    else:
        theta[t] = theta[t - 1]

ax1 = plt.subplot(211)
ax2 = plt.subplot(212) 
plt.sca(ax1)
plt.ylim(thetamin, thetamax)
plt.plot(range(T+1), theta, 'g-')
plt.sca(ax2)
num_bins = 50
plt.hist(theta, num_bins, normed=1, facecolor='red', alpha=0.5)
plt.show()

实验的结果：

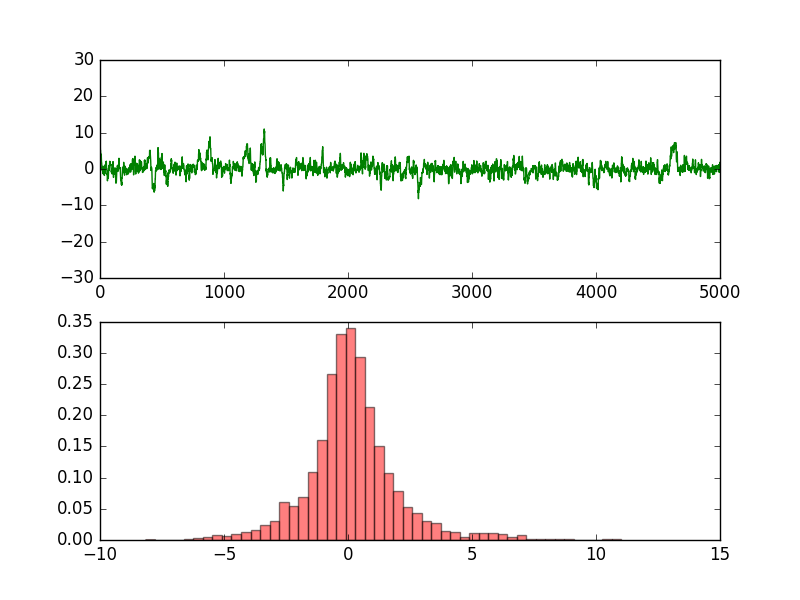
这里写图片描述

对于Metropolis采样算法，其要求选定的分布必须是对称的，为了弥补这样的一个缺陷，在下一篇中，介绍一下Metropolis-Hastings采样算法，其是Metropolis采样算法的推广形式。

简单易学的机器学习算法——马尔可夫链蒙特卡罗方法MCMC