
遗传算法(Genetic Algorithm)学习总结
最近学习了一下遗传算法,感觉非常有趣,就深入钻研了一下,这是一个非常适合用来求全局最优解的算法思想。这篇文章主要是和大家分享一下自己学习下来的一些总结,希望对大家的学习也能有一定价值。
概述
大自然的生存法则就是物竞天择,优胜劣汰,能够适应大自然,物种方可生存下去,得以繁衍。遗传算法(Genetic Algorithm,GA)便是沿用了这一思想,它是根据模仿自然界生物进化机制发展起来的随机全局搜索和优化方法,借鉴了达尔文的进化论和孟德尔的遗传学说。其本质是一种高效、并行、全局搜索的方法,能在搜索过程中自动获取和积累有关搜索空间的知识,并自适应地控制搜索过程以求得全局最优解。
关键术语
- 基因型(genotype):性状染色体的内部表。
- 表现型(phenotype):染色体决定的性状的外部表现,或者说,根据基因型形成的个体的外部表现。
- 适应度(fitness):度量某个物种对于生存环境的适应程度。
- 选择(selection):以一定的概率从种群中选择若干个个体。一般,选择过程是一种基于适应度的优胜劣汰的过程。
- 交叉配对(crossover):两个染色体的某一相同位置处DNA被切断,前后两串分别交叉组合形成两个新的染色体,也称基因重组或杂交。
- 变异(mutation):配对时DNA可能(很小的概率)产生某些细小的差错,变异产生新的染色体,表现出新的性状。
- 编码(coding):DNA中遗传信息在一个长链上按一定的模式排列。遗传编码可看作从表现型到基因型的映射。
- 解码(decoding):基因型到表现型的映射。
- 个体(individual):指染色体带有特征的实体。
- 种群(population):个体的集合,该集合内个体数称为种群。
- 代(generation):指染色体交叉配对将产生的后代代数。
引例
太过专业的定义大家还是很难明白遗传算法是什么,要干什么。那么我来给大家举个例子。想象一下有一群人生活在山中,他们随机地居住在山中的不同位置,有人在山峰,有人在山谷,有人在山腰。突然有一天发起了大水,水不停地向上涨,那些住在地势比较低地方的人们就会淹死,不排除极个别少数人水性比较好,能存活一阵子。而那些住在地势比较高地方的人就不会淹死,我们称那些不会淹死的人对环境的适应度较高。为了繁衍后代,就在这些适应度高的人群中进行交叉繁殖,希望在繁殖的过程中得到能够到达所有山峰中最高的山峰从而得以存活的最优一代的DNA,当然在繁殖过程中不排除有基因变异的可能存在。那么在这个问题中如何繁衍出生活在最高山峰的这代种群就是遗传算法所要解决的问题。
我们可以将整座山投影到二维平面,那么山的地形就如同这个函数图像,把人就当作图像中的点,那么我们只需要得出最高点的横坐标即可得知最优一代的DNA。


实现过程
遗传算法的实现过程就像是自然界生物的进化那样,只不过你就是自然规则的缔造者。首先制定人的DNA的编码方案,即建立基因型和表现型的映射关系。然后随机初始化一个种群,即人类,为其分配随机的DNA序列,即人们在山中的位置(图中点的横坐标),并将DNA依照自己建立的映射关系编码成表现型。接下来通过自己制定的适应度算法来算出处在不同位置的人的适应度,地势高的人适应度越高,越容易存活,而地势低的人适应度低,存活率也就低,每隔一段时间,适应度较低的人就会被大自然所淘汰以保证人类总体数目持平。随后,根据自己的择优方案按照适应度对人进行择优,再从这些存活的人中随机选择父母进行交叉配对,各选择父母的部分DNA进行基因重组产生新的DNA,从而得到一个处在不同位置的新生儿,为了避免人们生出了一个处在某个局部最高山峰的新生儿便以为这是最优一代的DNA就停止繁殖,我们允许新生儿有小概率变异的可能性。按照这个过程迭代N代,最终它将找到最适应这个环境的人的DNA。对于遗传算法而言,它并不知道它自己要做什么,它只是不断地在生成新的解,而你不需要告诉它怎么求得最好的解,只需要不断地否定其不好的解即可。
具体步骤
以下内容循环N次
- 评估每个个体的适应度。
- 依据适应度越高,被选择概率越大的原则,从种群中随机选择出父母。
- 让父母进行交叉配对,繁殖出子代。
- 对子代染色体进行变异,并取代父母。
1.基因编码方式
学过生物的朋友们都知道DNA是由碱基对构成的,受其启发,在计算机中我们可以认为“0”,“1”这两种二进制码就是构成DNA的碱基,再将他们串在一起就形成了一条可以表达个体特征的染色体。这就是二进制码编码,例如1011011000011011就是一条染色体。
二进制编码虽然简单直观,但当个体特征比较复杂时,需要很长的二进制码才足以精准描述,为了解决这个问题就引入了浮点数编码,例如3.2-1.1-4.9-0.5-7.1-3.8。
这里我以二进制编码为例。我们可以将二进制数转换成十进制数,再将其映射到指定区间,即可得到人所处的位置。例如1011011000011011转换成十进制是46619,那么在对应区间[0 , 5]上,其横坐标的值应该是:

2.适应度评估
为了刻画出个体在环境中的适应程度,我们需要制定一个适应度函数,这非常重要,关系到人该往哪个方向进化。适应度函数由你自己制定,在本例中,问题已经简化成找到该图像的最高点,因此适应度函数很好确定,位置越高的点,适应度就越高。我以表现型DNA作为输入,返回该值加上一个极小值再减去所有个体表现型DNA中最小的值,这么做的原因是图像上的高度有正有负,而算概率的时候不应该出现负值,所以减去负值之后所有值就都是正的了,再加上一个极小值是为了保证减去最小值后分母不会为0。当然这并不一定是最好的方法。
def get_fitness(result):
return result + 1e-9 - np.min(result)
3.选择函数
选择函数决定了哪些个体有生存并繁衍的权利,通常其规则是适应度越高的个体越有可能作为父母进行繁殖,而适应度越低的个体则越有可能被淘汰。通常选择函数的制定方法有以下几种:
- Proportionate Roulette Wheel Selection
- Linear Ranking Selection
- Exponential Ranking Selection
- Tournament Selection
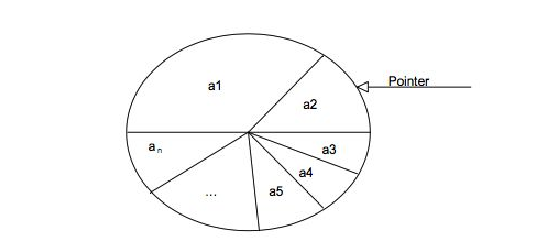
在实际应用中,最常见也是最易理解的方法就是Proportionate Roulette Wheel Selection(轮盘赌算法)。其原理就是将每个个体的适应度在整体适应度中的占比,再依据占比对个体进行选择,因此适应度高的个体占比就大,被选中的概率也就高。
def select(pop, fitness):
idx = np.random.choice(np.arange(POP_SIZE), size=POP_SIZE, replace=True,p=fitness/fitness.sum())
return pop[idx]
4.交叉配对
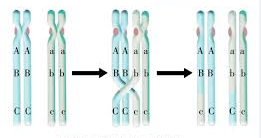
配对的过程就类似DNA基因片段的交换,从而生成新的个体。
5.基因变异
为了使得遗传算法具有局部的随机搜索能力以及避免陷入局部最优解,我们可以对生成的新DNA进行变异来使得DNA更加具有多样性。相应的,变异也分为实值变异和二进制变异。我以二进制变异为例,如果新生成的DNA是1001010100110101,那么可以将它某一位的0取成1或者1取成0,就变成了0001010100110101,同样这也取决于你制定的变异策略。由于变异具有随机性,因此我们无法断言变异会生成更好的DNA还是更坏的DNA。
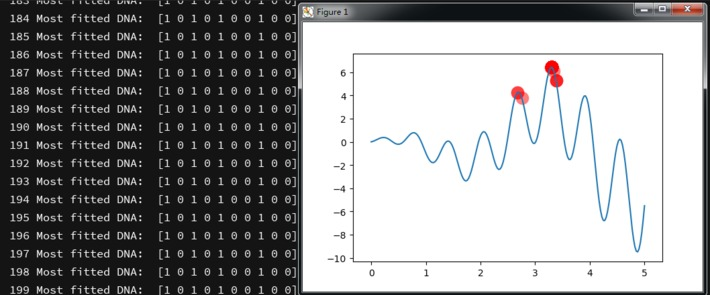
这是之前那个例子的运行结果。总共有100个个体,DNA长度为10位,交配成功率为0.8,变异率为0.003,迭代200次,最终找到了最大值点的DNA:[1 0 1 0 1 0 0 1 0 0]。(当新生一代的DNA为这个值时,将会在山顶成功存活,免于水灾。)至于图中为何没有所有点收敛于一点,我思考了一下,可能原因是每一次迭代都会进行交叉变异,虽然已经找到了最大值的点,但是仍然会有个别新生的DNA产生在局部最优位置,而种群中大部分的个体都已经收敛到了全局最优位置。(也可能是这个demo的实现算法还有需要改进的地方)
总结
遗传算法的编写核心就在于这几点的确立:编码,适应度评估,选择策略,交叉配对,基因变异。
在设计适应度函数时最容易遇到的问题就是欺骗问题,使得最终答案偏离全局最优解收敛至局部最优解,在这篇paper中就提出使用均匀设计法去解决欺骗问题,有兴趣的朋友可以研究一下。(均匀设计法在GA欺骗问题中的应用研究)
目前遗传算法可以应用的问题还有很多,例如旅行商人问题,排班问题,句子生成等,这些应用都非常有趣,有兴趣的朋友可以自己去编码实现一下。
参考
遗传算法GA(Genetic Algorithm)入门知识梳理
作者:Linx
本文仅代表个人的一些理解,若有描述不当的地方,欢迎指正!
码字不易,欢迎讨论,转载请注明出!。