人工神经网络(ANN)入门二这篇文章主要介绍了ANN的相关知识，其中包含多层人工神经网络、后向传输(backward p

在人工神经网络（ANN）入门一中我们可以用单层的人工神经网络解决AND和OR的运算。但是很多问题例如异或运算(exclusive-or)不能使用单层的神经网络找到这样一个线性平面把训练集中的数据分开。下面表格中是一个异或运算

x_1	x_2	output
1	1	-1
0	1	1
0	0	-1
1	0	1

将点在平面直角坐标系中画出来如下图：
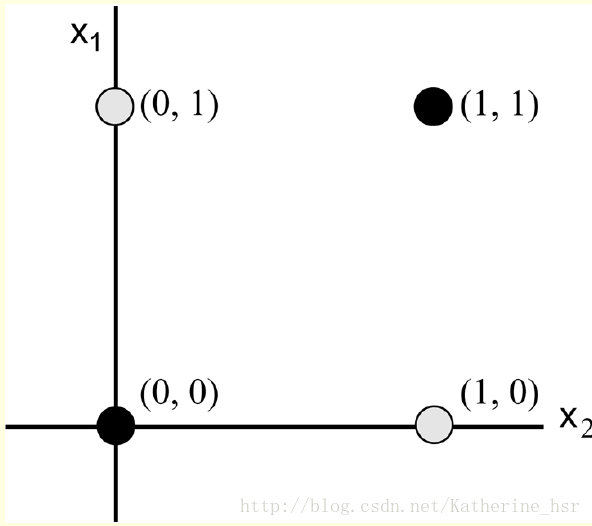
这里写图片描述
如图所示，黑色和灰色的点代表不同的分类，但是我们不能找到一个平面能将这两个分类分开，这时我们便需要多层人工神经网络。
首先我们来介绍下多层人工神经网络：
人工神经网络结构通常比感知器模型更近复杂，这些额外的复杂性来源与多个方面。
(1）网络的输入层和传输层之间可能包含多个中间层，这些中间层叫做隐藏层(hidden layer),隐藏层中间的节点称为隐藏节点(hedden node)。这种结构称为多层神经网络，如图所示。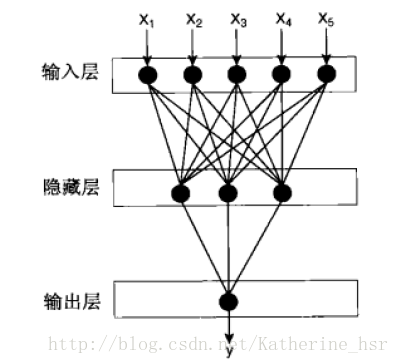这里写图片描述
在前向反馈(forward phase)中，1.每一层节点只和下一层节点相连，从前一次迭代中获得的权重用来计算每一个神经元的输出值。2.总是先计算l层，再计算l+1层。
(2)除了符号函数外，网络还可以使用其他激活函数，例如线性函数、S型(逻辑斯蒂)函数、双曲线正切函数等，如图所示。
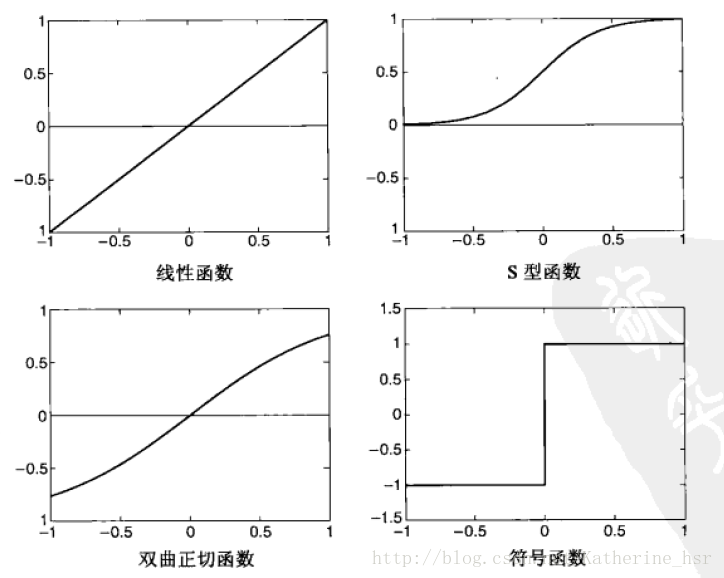
这里写图片描述
这些激活函数允许隐藏节点和输出节点的输出值与输入参数呈非线性关系。
这些附加的复杂性使得多层神经网络可以对输入和输出变量间更复杂的关系建模。例如上面提到的异或问题，我们可以用两个超平面进行分类，这两个超平面把输入空间划分到各自的类，如图：
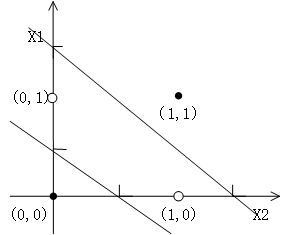
这里写图片描述
与人工神经网络（ANN）入门一中提到的计算方法类似，根据坐标系中画出的两条直线我们可以得到两组线性方程：
$x_2+x_1-0.5=0$
$-x_1-x_2+0.5=0$
和
$x_2+x_1-1.5=0$
$-x_1-x_2+1.5=0$
将表格中的数据带入到两组方程中，我们可以得到最终符合表格中输入与输出的两个线性方程为：
$x_2+x_1-0.5=0$ 和
$x_2+x_1-1.5=0$

输入层计算出的结果的输出便为中间层的输入，我们可以将中间层的数据也表示出来：

x_1	x_2	h_1	h_2	output
0	0	-1	-1	-1
0	1	1	-1	1
1	0	1	-1	1
1	1	1	1	-1

我们可以将 $h_1, h_2$ 的点也在直角坐标系中的表示出来，如图：
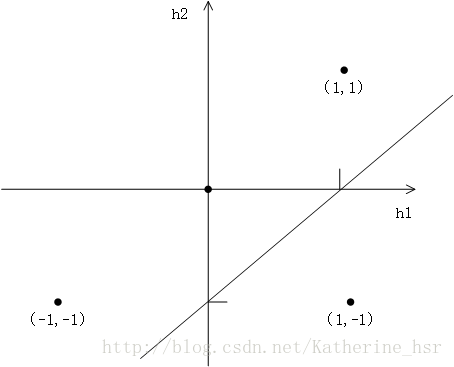
这里写图片描述
同样我们可以根据图中的直线得到两个方程：
$h_1-h_2-1=0$
$h_2-h_1+1=0$
将图中的点带入到方程中，可以验证方程 $h_1-h_2-1=0$ 是符合条件的方程式。
现在我们可以将双层感知器的构造图画出来了
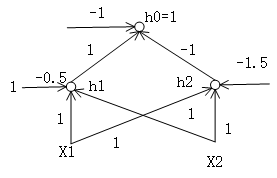
这里写图片描述
接下来我们要介绍一个神经网络中一个很重要的概念后向传输(backward phase)，后向传输算法是专门为多层神经网络设计的。在后向传播的过程中，先更新l+1层的权重，再更新l层的权重。学习方法允许我们利用l+1层的的错误率来估算l层的错误率。
一个常见的激活函数就是双曲正切函数(hyperbolic tangent function)
$f(net)=\frac{e^{net}-e^{-net}}{e^{net}+e^{-net}}=\frac{e^{2(net)}-1}{e^{2(net)}+1}$
图像如下图：
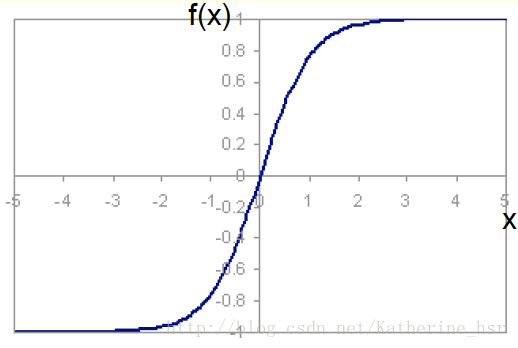
这里写图片描述
由图像可以看出来，当net趋近于无穷大时，f(net)趋近于1；当net趋近于负无穷大时，f(net)趋近于-1.
这个函数中一个重要的性质是它是可以微分的
$f'(net)=1-[f(net)]^2$
它的导数就代表斜率。当net趋近于无穷时，斜率为0；当net趋近于负无穷时，斜率为0；当net=0时，斜率为1。
反向传播学习是基于错误平面(error surface)的概念，这个平面代表了作为网络权重函数的一个数据集的错误的累计，每一个可能的网络权重设置被平面上的一个点来表示出来。这个反向学习算法的目标就是去决定一组能使误差最小的权重的集合，所以这个算法应该被设计为在平面上找到一个能使错误迅速减小的方向。我们能够通过梯度下降(gradient descent learning)的方法在平面上找到这个点，这种方法的主要思想就是在平面上的每一个点向相反方向移动梯度向量。
下图为一个错误平面，横坐标代表权重，纵坐标代表误差。在平面上由权重为W1 old的点反向移动梯度向量到W1new，可以发现W1 new的斜率小于W1 old，所以相对于W1 old来说，W1 new更满足我们的要求(在平面上找到一个能使错误迅速减小的方向)。然后继续反向移动梯度向量，可以发现可能在某个点(图中为local minimum)上斜率为0，但是这一点未必为最优的权重。在训练过程中有时局部最优解也是可以被接受的。
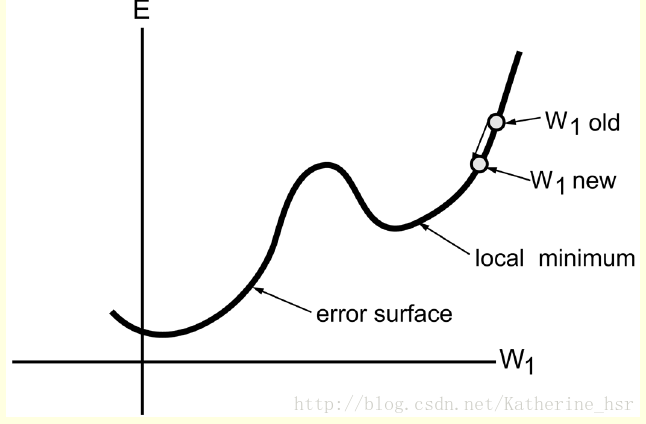
这里写图片描述
误差能够通过计算每一个输出点的误差的平方和来计算，公式为:

E =1 2 ∑ n =0 n =∞ (d k −o k ) 2 E=12∑n=0n=∞(dk−ok)2
其中， $d_k$ 代表第k个点实际应该输出的结果， $o_k$ 代表第k个点实际输出的结果。
对于第j个点的第i个权重，梯度下降操作可以表示为：
Δ w i j =− cδ E δ w i j Δwij=−cδEδwij
在这个方程中可以看出，偏微分就用来判断第j个点的第i个权重的错误的变化率。这个偏微分的判断需要一个可以微分的激活函数。
对于多层神经网络来说，我们假设第j层隐藏层的点为 $h_j$ ，对于输出节点和隐藏节点我们需要两个方程去调整权重，假设只有一个隐藏层，则输出层的节点：
Δ u j k =c (d k −o k )(1 −o 2 k )h j Δujk=c(dk−ok)(1−ok2)hj
对于隐藏层节点：
$\Delta w_{ij}=c(1-h_j^2)[\sum_k(u_{jk}\delta_k)]x_i$
这个方程中
$\delta =(d_k-o_k)(1-o_k^2)$
基本的人工神经网络的知识就介绍完了，总结一下神经网络的特点吧：
(1)至少含有一个隐藏层的多层神经网络是一种普适近似(universal approximator)，即可用用来近似任何目标函数。
(2)梯度下降方法经常会收敛到局部极小值，避免局部极小值的方法是在权值更新公式中加一个动量项(momentum term).
(3)人工神经网络可以处理冗余特征，因为权值在训练过程中自动学习，冗余特征的权值非常小。
(4)训练人工神经网络是一个很耗时的过程，特别是当隐藏节点数量很大的时候。