绘制镜像线条了解一下?

flowers1225
848 阅读3分钟

功能需求：“用户绘制一条线，然后镜像出另外一条线。”

下面是我实现的过程，怕以后要用，就记下来了。

首先对问题的描述转化了一下：“求p(x, y)点， 关于直线p1(x1, y1), p2(x2, y2)镜像 得到P(Px, Py)” 。

带着这个问题开始思考，也在网上找了一些数学计算的公式。

step1 分析

先求关于点p1,p2的直线方程。（直线的一般方程Ax + By + C = 0）

关于直线p1,p2对称有以下几种形式：

  • 关于X轴的对称

    (p1.x = p2.x) 可知 直线(p1 p2) 与X轴垂直，得到直线方程 x = p1.x;

  • 关于Y轴的对称

    (p1.y = p2.y) 可知 直线(p1 p2) 与Y轴垂直，得到直线方程 y = p1.y;

  • 关于某直线(p1, p2)的对称

    (p1.x != p2.x) && (p1.y != p2.y) 带入两点式 (y - p1.y) / (p2.y - p1.y) = (x - p1.x) / (p2.x - p1.x)

    直线(p1, p2)的斜率为 k = (p2.y - p1.y) / (p2.x - p1.x)

    得到直线方程：y = k * (x - p1.x) + p1.y;

step2 计算

求计算（p.x, p.y）关于直线Ax + By + C = 0对称的点：

Px = p.x - 2 * A (A * p.x + B * p.y + C) / (A^2 + B^2);
Py = p.y - 2 * B (A * p.x + B * p.y + C) / (A^2 + B^2);

  • 关于X轴的对称

    有直线方程 x - p1.x = 0 得 A = 1, B = 0, C = -p1.x,带入对称点计算公式得到

    Px = 2 * p1.x - p.x;

Py = p.y;

  • 关于Y轴的对称

    有直线方程 y - p1.y = 0 得 A = 0, B = 1, C = -p1.y,带入对称点计算公式得到

    Px = p.x;
 
Py = 2 * p1.y - p.y;

  • 关于某直线(p1, p2)的对称

    有直线方程 y = k * (x - p1.x) + p1.y 得 A = k, B = -1, C = -k * p1.x + p1.y,带入对称点计算公式得到

     Px = p.x - 2 * k * ( k * p.x - p.y + (-k * p1.x + p1.y)) / (Math.pow(k, 2) + 1);
 
 Py = p.y - 2 * -1 * ( k * p.x - p.y + (-k * p1.x + p1.y)) / (Math.pow(k, 2) + 1);

step3 绘制

点的公式都得到了，剩下的就是canvas绘制了。canvas的绘制这里就不多讲，直接写个demo直观点。

  • 建立直线
// 这里我绘制三条轴的起始点和终点（两点确定一条直线），便于观察绘制的图形。

let canvasWidth = ctx.canvas.width;
let canvasHeight = ctx.canvas.height;
        
let axleX = {
    start: {
        x: canvasWidth,
        y: canvasHeight / 2
    },
    end: {
        x: 0,
        y: canvasHeight / 2
    }
};

let axleY = {
    start: {
        x: canvasWidth / 2,
        y: 0
    },
    end: {
        x: canvasWidth / 2,
        y: canvasHeight
    }
};

let axle = {
    start: {
        x: canvasWidth,
        y: 0
    },
    end: {
        x: 0,
        y: canvasHeight

    }
};

function drawAxle () {
    ctx.lineWidth = 1;
    ctx.lineJoin = ctx.lineCap = 'round';

    ctx.strokeStyle = '#000';

    ctx.beginPath();
    // x
    ctx.moveTo(axleX.start.x, axleX.start.y);
    ctx.lineTo(axleX.end.x, axleX.end.y);
    ctx.stroke();

    // y
    ctx.beginPath();
    ctx.moveTo(axleY.start.x, axleY.start.y);
    ctx.lineTo(axleY.end.x, axleY.end.y);
    ctx.stroke();

    // 对角
    ctx.beginPath();
    ctx.moveTo(axle.start.x, axle.start.y);
    ctx.lineTo(axle.end.x, axle.end.y);
    ctx.stroke();
};

drawAxle();

分别关于X轴、Y轴、任意线（这里对角线为例子）

图一

  • 计算对称点（核心）

    由上述得到公式得到。

    function calcSymmetryPoint (p1, p2, p) {

    if (p1.x  ==  p2.x) {
    	 // 关于Y轴镜像
        return   {
            x: 2 * p1.x - p.x,
            y: p.y
        }
    } else if (p1.y  ==  p2.y) {
        // 关于X轴镜像
        return   {
            x: p.x,
            y: 2 * p1.y - p.y
        }
    }
    
    //  关于任意直线镜像
    let k1 = (p2.y - p1.y) / (p2.x - p1.x);
    
    let x = p.x - 2 * k1 * ( k1 * p.x - p.y + (-k1 * p1.x + p1.y))/ (Math.pow(k1, 2) + 1);
    let y = p.y - 2 * -1 * ( k1 * p.x - p.y + (-k1 * p1.x + p1.y))/ (Math.pow(k1, 2) + 1);
    
	return   {
        x: x,
        y: y
    }
}

  • 绘制

    伪代码如下：

    ...

  function mousemoveHandler (event) {
  	// 得到需要镜像的点(p.x, p.y)
  	let x = e.clientX - (w - canvasWidth) / 2;
  	let y = e.clientY - (h - canvasHeight) / 2;
  	  
  	// 得到镜像之后点的(Px,Py)
  	calcSymmetryPoint({x: axleX.start.x, y: axleX.start.y}, {x: axleX.end.x, y: axleX.end.y}, {x: x, y: y});

    calcSymmetryPoint({x: axleY.start.x, y: axleY.start.y}, {x: axleY.end.x, y: axleY.end.y}, {x: x, y: y});

    calcSymmetryPoint({x: axle.start.x, y: axle.start.y}, {x: axle.end.x, y: axle.end.y}, {x: x, y: y}); 
  	  
  	// 绘制.. 
  	// ctx.beginPath();
  	// ctx.moveTo(...);
  	// ctx.lineTo(...);
  	// ctx.stroke();
}

...

    效果演示如下：

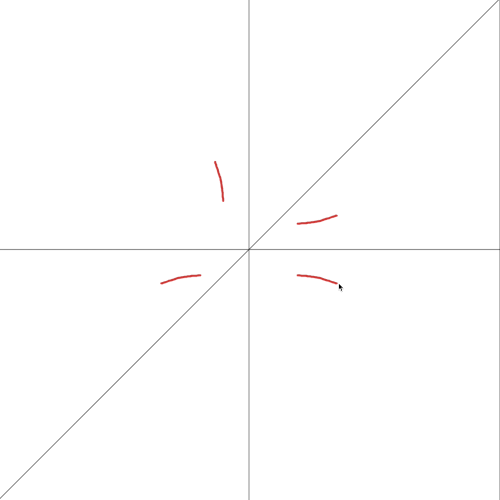图二

这里只是重点描述一下怎么计算镜像点的坐标，（计算的方式还有矩阵）我们可以用这个来做很多有趣的效果动画，另外也可以拓展到3d空间里去做镜像。

参考：

斜率： zh.wikipedia.org/wiki/%E6%96…

直线方程：zh.wikipedia.org/wiki/%E7%9B…

直线方程：baike.baidu.com/item/%E7%9B…

my_blog: www.flowers1225.com/

avatar
文章
阅读
粉丝